湘教版 八年级数学下学期期末模拟卷8（含解析）

这是一份湘教版 八年级数学下学期期末模拟卷8（含解析），共19页。

A．第一象限B．第二象限C．第三象限D．第四象限
2．（3分）下列几组数中，不能作为直角三角形三边长度的是（ ）
A．3，4，5B．5，7，8C．8，15，17D．1，
3．（3分）在平面直角坐标系中，点（4，﹣3）关于y轴对称的点的坐标是（ ）
A．（﹣4，﹣3）B．（4，3）C．（﹣4，3）D．（4，﹣3）
4．（3分）将直线y＝2x﹣1向上平移2个单位长度，可得直线的解析式为（ ）
A．y＝2x﹣3B．y＝2x﹣2C．y＝2x+1D．y＝2x
5．（3分）矩形的对角线长为10，两邻边之比为3：4，则矩形的面积为（ ）
A．12B．24C．48D．50
6．（3分）一次函数y＝（k﹣3）x+2，若y随x的增大而增大，则k的值可以是（ ）
A．1B．2C．3D．4
7．（3分）已知一次函数的图象过点（0，3）和（﹣2，0），那么直线必过下面的点（ ）
A．（4，6）B．（﹣4，﹣3）C．（6，9）D．（﹣6，6）
8．（3分）一次函数y＝kx+k的图象可能是（ ）
A．B．C．D．
9．（3分）下列字母中既是中心对称图形又是轴对称图形的是（ ）
A．B．C．D．
10．（3分）下列命题中，错误的是（ ）
A．平行四边形的对角线互相平分
B．菱形的对角线互相垂直平分
C．矩形的对角线相等且互相垂直平分
D．角平分线上的点到角两边的距离相等
二、填空题（本题共8小题，每小题3分，共24分)
11．（3分）函数y＝（k+1）x﹣7中，当k满足 时，它是一次函数．
12．（3分）已知一组数据有40个，把它分成六组，第一组到第四组的频数分别是10，5，7，6，第五组的频率是0.2，则第六组的频率是 ．
13．（3分）有一个多边形的内角和是它外角和的5倍，则这个多边形是 边形．
14．（3分）菱形的周长是20，一条对角线的长为6，则它的面积为 ．
15．（3分）如图，AD∥BC，∠ABC的角平分线BP与∠BAD的角平分线AP相交于点P，作PE⊥AB于点E．若PE＝2，则两平行线AD与BC间的距离为 ．
16．（3分）如图所示，将四根木条组成的矩形木框变成▱ABCD的形状，并使其面积变为原来的一半，则这个平行四边形的一个最小的内角的度数是 ．
17．（3分）如图所示，矩形纸片ABCD中，AB＝4cm，BC＝8cm，现将其沿EF对折，使得点C与点A重合，则AF的长为 ．
18．（3分）如图，在平面直角坐标系中，矩形OABC的对角线AC平行于x轴，边OA与x轴正半轴的夹角为30°，OC＝2，则点B的坐标是 ．
三、解答题（本大題共8小题，共66分)
19．（6分）如图所示，点E，F是平行四边形ABCD对角线BD上的点，BF＝DE，求证：AE＝CF．
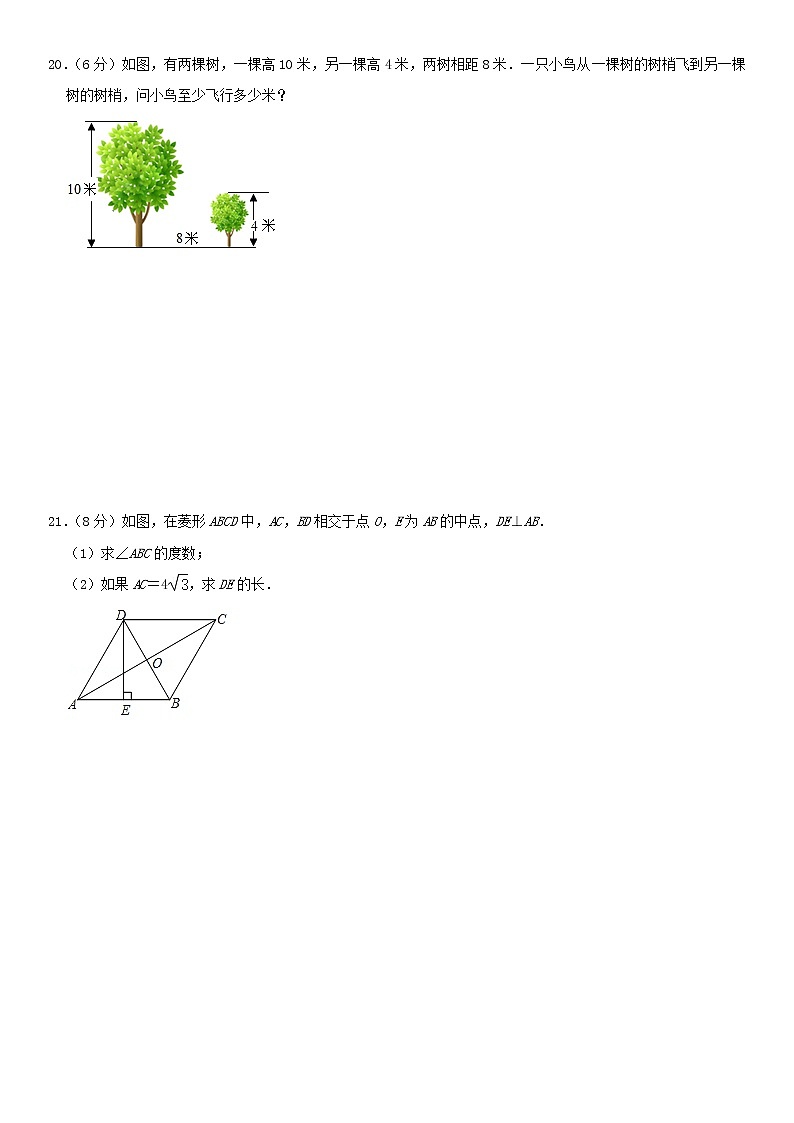
20．（6分）如图，有两棵树，一棵高10米，另一棵高4米，两树相距8米．一只小鸟从一棵树的树梢飞到另一棵树的树梢，问小鸟至少飞行多少米？
21．（8分）如图，在菱形ABCD中，AC，BD相交于点O，E为AB的中点，DE⊥AB．
（1）求∠ABC的度数；
（2）如果AC＝4，求DE的长．
22．（8分）为创建“国家园林城市”，某校举行了以“爱我黄石”为主题的图片制作比赛，评委会对200名同学的参赛作品打分发现，参赛者的成绩x均满足50≤x＜100，并制作了频数分布直方图，如图．
根据以上信息，解答下列问题：
（1）请补全频数分布直方图；
（2）若依据成绩，采取分层抽样的方法，从参赛同学中抽40人参加图片制作比赛总结大会，则从成绩80≤x＜90的选手中应抽多少人？
（3）比赛共设一、二、三等奖，若只有25%的参赛同学能拿到一等奖，则一等奖的分数线是多少？
23．（8分）如图，△ABC三个顶点的坐标分别为A（1，1），B（4，2），C（3，4）．
（1）请画出△ABC向左平移5个单位长度后得到的△A1B1C1；
（2）请画出△ABC关于原点对称的△A2B2C2；
（3）在x轴上求作一点P，使△PAB的周长最小，请画出△PAB，并直接写出P的坐标．
24．（8分）为了响应国家节能减排的号召，鼓励市民节约用电，我市从2012年7月1日起，居民用电实行“一户一表”的“阶梯电价”，分三个档次收费，第一档是用电量不超过180千瓦时实行“基本电价”，第二、三档实行“提高电价”，具体收费情况如右折线图，请根据图象回答下列问题；
（1）当用电量是180千瓦时时，电费是 元；
（2）第二档的用电量范围是 ；
（3）“基本电价”是 元/千瓦时；
（4）小明家8月份的电费是328.5元，这个月他家用电多少千瓦时？
25．（10分）将两个全等的直角三角形ABC和DBE按图①方式摆放，其中∠ACB＝∠DEB＝90°，∠A＝∠D＝30°，点E落在AB上，DE所在直线交AC所在直线于点F．
（1）连接BF，求证：CF＝EF．
（2）若将图①中的△DBE绕点B按顺时针方向旋转角α，且0°＜α＜60°，其他条件不变，如图②，求证：AF+EF＝DE．
（3）若将图①中的△DBE绕点B按顺时针方向旋转角β，且60°＜β＜180°，其他条件不变，如图③，你认为（2）中的结论还成立吗？若成立，写出证明过程；若不成立，请直接写出AF、EF与DE之间的数量关系．
26．（12分）如图，在Rt△ABC中，∠B＝90°，AC＝60cm，∠A＝60°，点D从点C出发沿CA方向以4cm/s的速度向点A匀速运动，同时点E从点A出发沿AB方向以2cm/s的速度向点B匀速运动，当其中一个点到达终点时，另一个点也随之停止运动．设点D、E运动的时间是ts．过点D作DF⊥BC于点F，连接DE、EF．
（1）求证：AE＝DF；
（2）四边形AEFD能够成为菱形吗？如果能，求出相应的t值；如果不能，请说明理由；
（3）当t为何值时，△DEF为直角三角形？请说明理由．
期末模拟卷（8）
参考答案与试题解析
一、选择题（每小题有且只有一个正确答案，本题共10小题，每小题3分，共30分)
1．（3分）在平面直角坐标系中，点（﹣2，1）在（ ）
A．第一象限B．第二象限C．第三象限D．第四象限
【解答】解：点（﹣2，1）在第二象限，
故选：B．
2．（3分）下列几组数中，不能作为直角三角形三边长度的是（ ）
A．3，4，5B．5，7，8C．8，15，17D．1，
【解答】解：A、32+42＝52，符合勾股定理的逆定理，能作为直角三角形三边长度；
B、52+72≠82，不符合勾股定理的逆定理，不能作为直角三角形三边长度；
C、82+152＝172，符合勾股定理的逆定理，能作为直角三角形三边长度；
D、12+（）2＝（）2，符合勾股定理的逆定理，能作为直角三角形三边长度．
故选：B．
3．（3分）在平面直角坐标系中，点（4，﹣3）关于y轴对称的点的坐标是（ ）
A．（﹣4，﹣3）B．（4，3）C．（﹣4，3）D．（4，﹣3）
【解答】解：点（4，﹣3）关于y轴的对称点的坐标是（﹣4，﹣3），
故选：A．
4．（3分）将直线y＝2x﹣1向上平移2个单位长度，可得直线的解析式为（ ）
A．y＝2x﹣3B．y＝2x﹣2C．y＝2x+1D．y＝2x
【解答】解：原直线的k＝2，b＝﹣1；向上平移2个单位长度，得到了新直线，
那么新直线的k＝2，b＝﹣1+2＝1．
∴新直线的解析式为y＝2x+1．
故选：C．
5．（3分）矩形的对角线长为10，两邻边之比为3：4，则矩形的面积为（ ）
A．12B．24C．48D．50
【解答】解：∵矩形的两邻边之比为3：4，
∴设矩形的两邻边长分别为：3x，4x，
∵对角线长为10，
∴（3x）2+（4x）2＝102，
解得：x＝2，
∴矩形的两邻边长分别为：6，8；
∴矩形的面积为：6×8＝48．
故选：C．
6．（3分）一次函数y＝（k﹣3）x+2，若y随x的增大而增大，则k的值可以是（ ）
A．1B．2C．3D．4
【解答】解：根据一次函数的性质，对于y＝（k﹣3）x+2，
当（k﹣3）＞0时，即k＞3时，y随x的增大而增大，
分析选项可得D选项正确．
故选：D．
7．（3分）已知一次函数的图象过点（0，3）和（﹣2，0），那么直线必过下面的点（ ）
A．（4，6）B．（﹣4，﹣3）C．（6，9）D．（﹣6，6）
【解答】解：设经过两点（0，3）和（﹣2，0）的直线解析式为y＝kx+b，
则，解得，∴y＝x+3；
A、当x＝4时，y＝×4+3＝9≠6，点不在直线上；
B、当x＝﹣4时，y＝×（﹣4）+3＝﹣3，点在直线上；
C、当x＝6时，y＝×6+3＝12≠9，点不在直线上；
D、当x＝﹣6时，y＝×（﹣6）+3＝﹣6≠6，点不在直线上；
故选：B．
8．（3分）一次函数y＝kx+k的图象可能是（ ）
A．B．
C．D．
【解答】解：当k＞0时，函数图象经过一、二、三象限；
当k＜0时，函数图象经过二、三、四象限，故B正确．
故选：B．
9．（3分）下列字母中既是中心对称图形又是轴对称图形的是（ ）
A．B．C．D．
【解答】解：A、是轴对称图形，也是中心对称图形，故此选项正确；
B、是轴对称图形，不是中心对称图形，故此选项错误；
C、不是轴对称图形，也不是中心对称图形，故此选项错误；
D、不是轴对称图形，是中心对称图形，故此选项错误．
故选：A．
10．（3分）下列命题中，错误的是（ ）
A．平行四边形的对角线互相平分
B．菱形的对角线互相垂直平分
C．矩形的对角线相等且互相垂直平分
D．角平分线上的点到角两边的距离相等
【解答】解：A、平行四边形的对角线互相平分，所以A选项的说法正确；
B、菱形的对角线互相垂直平分，所以B选项的说法正确；
C、矩形的对角线相等且互相平分，所以C选项的说法错误；
D、角平分线上的点到角两边的距离相等，所以D选项的说法正确．
故选：C．
二、填空题（本题共8小题，每小题3分，共24分)
11．（3分）函数y＝（k+1）x﹣7中，当k满足 k≠﹣1 时，它是一次函数．
【解答】解：根据一次函数定义得，k+1≠0，
解得k≠﹣1．
故答案为：k≠﹣1．
12．（3分）已知一组数据有40个，把它分成六组，第一组到第四组的频数分别是10，5，7，6，第五组的频率是0.2，则第六组的频率是 0.1 ．
【解答】解：根据第五组的频率是0.2，其频数是40×0.2＝8；
则第六组的频数是40﹣（10+5+7+6+8）＝4．
故第六组的频率是，即0.1．
13．（3分）有一个多边形的内角和是它外角和的5倍，则这个多边形是 12 边形．
【解答】解：根据题意，得
（n﹣2）•180＝5×360，
解得：n＝12．
所以此多边形的边数为12．
14．（3分）菱形的周长是20，一条对角线的长为6，则它的面积为 24 ．
【解答】解：∵菱形的周长是20
∴边长＝5
∵一条对角线的长为6
∴另一条对角线的长为8
∴菱形的面积＝×6×8＝24．
故答案为24．
15．（3分）如图，AD∥BC，∠ABC的角平分线BP与∠BAD的角平分线AP相交于点P，作PE⊥AB于点E．若PE＝2，则两平行线AD与BC间的距离为 4 ．
【解答】解：过点P作MN⊥AD，
∵AD∥BC，∠ABC的角平分线BP与∠BAD的角平分线AP相交于点P，PE⊥AB于点E，
∴AP⊥BP，PN⊥BC，
∴PM＝PE＝2，PE＝PN＝2，
∴MN＝2+2＝4．
故答案为：4．
16．（3分）如图所示，将四根木条组成的矩形木框变成▱ABCD的形状，并使其面积变为原来的一半，则这个平行四边形的一个最小的内角的度数是 30° ．
【解答】解：过A作AE⊥BC于点E，如图所示：
由四根木条组成的矩形木框变成▱ABCD的形状，面积变为原来的一半，
得到AE＝AB，又△ABE为直角三角形，
∴∠ABE＝30°，
则平行四边形中最小的内角为30°．
故答案为：30°
17．（3分）如图所示，矩形纸片ABCD中，AB＝4cm，BC＝8cm，现将其沿EF对折，使得点C与点A重合，则AF的长为 5cm ．
【解答】解：设AF＝xcm，则DF＝（8﹣x）cm，
∵矩形纸片ABCD中，AB＝4cm，BC＝8cm，现将其沿EF对折，使得点C与点A重合，
∴DF＝D′F，
在Rt△AD′F中，∵AF2＝AD′2+D′F2，
∴x2＝42+（8﹣x） 2，
解得：x＝5（cm）．
故答案为：5cm
18．（3分）如图，在平面直角坐标系中，矩形OABC的对角线AC平行于x轴，边OA与x轴正半轴的夹角为30°，OC＝2，则点B的坐标是 （2，） ．
【解答】解：过点B作BE⊥OE于E，
∵矩形OABC的对角线AC平行于x轴，边OA与x轴正半轴的夹角为30°，
∴∠CAO＝30°，
∴AC＝4，
∴OB＝AC＝4，
由矩形的性质可知∠BOA＝∠CAO＝30°，
∴∠OBE＝180°﹣30°﹣30°﹣90°＝30°，
∴OE＝2，
∴BE＝2，
∴则点B的坐标是（2，），
故答案为：（2，）．
三、解答题（本大題共8小题，共66分)
19．（6分）如图所示，点E，F是平行四边形ABCD对角线BD上的点，BF＝DE，求证：AE＝CF．
【解答】证明：∵四边形ABCD是平行四边形，
∴AD∥BC，AD＝BC，
∴∠EDA＝∠FBC，
在△AED和△CFB中，
，
∴△AED≌△CFB（SAS），
∴AE＝CF．
20．（6分）如图，有两棵树，一棵高10米，另一棵高4米，两树相距8米．一只小鸟从一棵树的树梢飞到另一棵树的树梢，问小鸟至少飞行多少米？
【解答】解：如图，设大树高为AB＝10m，
小树高为CD＝4m，
过C点作CE⊥AB于E，则EBDC是矩形，
连接AC，
∴EB＝4m，EC＝8m，AE＝AB﹣EB＝10﹣4＝6m，
在Rt△AEC中，AC＝＝10m，
故小鸟至少飞行10m．
21．（8分）如图，在菱形ABCD中，AC，BD相交于点O，E为AB的中点，DE⊥AB．
（1）求∠ABC的度数；
（2）如果AC＝4，求DE的长．
【解答】解：（1）∵E为AB的中点，DE⊥AB，
∴AD＝DB，
∵四边形ABCD是菱形，
∴AB＝AD，
∴AD＝DB＝AB，
∴△ABD为等边三角形．
∴∠DAB＝60°．
∵菱形ABCD的边AD∥BC，
∴∠ABC＝180°﹣∠DAB＝180°﹣60°＝120°，
即∠ABC＝120°；
（2）∵四边形ABCD是菱形，
∴BD⊥AC于O，AO＝AC＝×4＝2，
由（1）可知DE和AO都是等边△ABD的高，
∴DE＝AO＝2．
22．（8分）为创建“国家园林城市”，某校举行了以“爱我黄石”为主题的图片制作比赛，评委会对200名同学的参赛作品打分发现，参赛者的成绩x均满足50≤x＜100，并制作了频数分布直方图，如图．
根据以上信息，解答下列问题：
（1）请补全频数分布直方图；
（2）若依据成绩，采取分层抽样的方法，从参赛同学中抽40人参加图片制作比赛总结大会，则从成绩80≤x＜90的选手中应抽多少人？
（3）比赛共设一、二、三等奖，若只有25%的参赛同学能拿到一等奖，则一等奖的分数线是多少？
【解答】解：（1）200﹣（35+40+70+10）＝45，如下图：
（2）设抽了x人，则，解得x＝8；
（3）依题意知获一等奖的人数为200×25%＝50（人）．
则一等奖的分数线是80分．
23．（8分）如图，△ABC三个顶点的坐标分别为A（1，1），B（4，2），C（3，4）．
（1）请画出△ABC向左平移5个单位长度后得到的△A1B1C1；
（2）请画出△ABC关于原点对称的△A2B2C2；
（3）在x轴上求作一点P，使△PAB的周长最小，请画出△PAB，并直接写出P的坐标．
【解答】解：（1）△A1B1C1如图所示；
（2）△A2B2C2如图所示；
（3）△PAB如图所示，P（2，0）．
24．（8分）为了响应国家节能减排的号召，鼓励市民节约用电，我市从2012年7月1日起，居民用电实行“一户一表”的“阶梯电价”，分三个档次收费，第一档是用电量不超过180千瓦时实行“基本电价”，第二、三档实行“提高电价”，具体收费情况如右折线图，请根据图象回答下列问题；
（1）当用电量是180千瓦时时，电费是 108 元；
（2）第二档的用电量范围是 180＜x≤450 ；
（3）“基本电价”是 0.6 元/千瓦时；
（4）小明家8月份的电费是328.5元，这个月他家用电多少千瓦时？
【解答】解：（1）由函数图象，得
当用电量为180千瓦时，电费为：108元．
故答案为：108；
（2）由函数图象，得
设第二档的用电量为x千瓦时，则180＜x≤450．
故答案为：180＜x≤450；
（3）基本电价是：108÷180＝0.6；
故答案为：0.6
（4）设直线BC的解析式为y＝kx+b，由图象，得
，
解得：，
y＝0.9x﹣121.5．
y＝328.5时，
x＝500．
答：这个月他家用电500千瓦时．
25．（10分）将两个全等的直角三角形ABC和DBE按图①方式摆放，其中∠ACB＝∠DEB＝90°，∠A＝∠D＝30°，点E落在AB上，DE所在直线交AC所在直线于点F．
（1）连接BF，求证：CF＝EF．
（2）若将图①中的△DBE绕点B按顺时针方向旋转角α，且0°＜α＜60°，其他条件不变，如图②，求证：AF+EF＝DE．
（3）若将图①中的△DBE绕点B按顺时针方向旋转角β，且60°＜β＜180°，其他条件不变，如图③，你认为（2）中的结论还成立吗？若成立，写出证明过程；若不成立，请直接写出AF、EF与DE之间的数量关系．
【解答】（1）证明：如图1，连接BF，
∵△ABC≌△DBE，
∴BC＝BE，
∵∠ACB＝∠DEB＝90°，
在Rt△BCF和Rt△BEF中，
，
∴Rt△BCF≌Rt△BEF（HL），
∴CF＝EF；
（2）如图2，连接BF，
∵△ABC≌△DBE，
∴BC＝BE，
∵∠ACB＝∠DEB＝90°，
在Rt△BCF和Rt△BEF中，
，
∴Rt△BCF≌Rt△BEF（HL），
∴EF＝CF，
∴AF+EF＝AF+CF＝AC＝DE；
（3）如图3，连接BF，
∵△ABC≌△DBE，
∴BC＝BE，
∵∠ACB＝∠DEB＝90°，
∴△BCF和△BEF是直角三角形，
在Rt△BCF和Rt△BEF中，
，
∴Rt△BCF≌Rt△BEF（HL），
∴CF＝EF，
∵AC＝DE，
∴AF＝AC+FC＝DE+EF．
26．（12分）如图，在Rt△ABC中，∠B＝90°，AC＝60cm，∠A＝60°，点D从点C出发沿CA方向以4cm/s的速度向点A匀速运动，同时点E从点A出发沿AB方向以2cm/s的速度向点B匀速运动，当其中一个点到达终点时，另一个点也随之停止运动．设点D、E运动的时间是ts．过点D作DF⊥BC于点F，连接DE、EF．
（1）求证：AE＝DF；
（2）四边形AEFD能够成为菱形吗？如果能，求出相应的t值；如果不能，请说明理由；
（3）当t为何值时，△DEF为直角三角形？请说明理由．
【解答】（1）证明：∵在Rt△ABC中，∠B＝90°，AC＝60cm，∠A＝60°，
∴∠C＝90°﹣∠A＝30°．
∵CD＝4tcm，AE＝2tcm，
又∵在直角△CDF中，∠C＝30°，
∴DF＝CD＝2tcm，
∴DF＝AE；
（2）解：∵DF∥AB，DF＝AE，
∴四边形AEFD是平行四边形，
当AD＝AE时，四边形AEFD是菱形，
即60﹣4t＝2t，
解得：t＝10，
即当t＝10时，▱AEFD是菱形；
（3）解：当t＝时△DEF是直角三角形（∠EDF＝90°）；
当t＝12时，△DEF是直角三角形（∠DEF＝90°）．
理由如下：
当∠EDF＝90°时，DE∥BC．
∴∠ADE＝∠C＝30°
∴AD＝2AE
∵CD＝4tcm，
∴DF＝AE＝2tcm，
∴AD＝2AE＝4tcm，
∴4t+4t＝60，
∴t＝时，∠EDF＝90°．
当∠DEF＝90°时，DE⊥EF，
∵四边形AEFD是平行四边形，
∴AD∥EF，
∴DE⊥AD，
∴△ADE是直角三角形，∠ADE＝90°，
∵∠A＝60°，
∴∠DEA＝30°，
∴AD＝AE，
AD＝AC﹣CD＝60﹣4t（cm），AE＝DF＝CD＝2tcm，
∴60﹣4t＝t，
解得t＝12．
综上所述，当t＝时△DEF是直角三角形（∠EDF＝90°）；当t＝12时，△DEF是直角三角形（∠DEF＝90°）．