人教版九年级上册24.3 正多边形和圆备课课件ppt

这是一份人教版九年级上册24.3 正多边形和圆备课课件ppt，共26页。PPT课件主要包含了新课导入，正多边形，正多边形和圆，∴∠A∠B，中心角，半径R，边心距r，正多边形的相关概念，边心距，正多边形的外角等内容，欢迎下载使用。
三条边相等,三个角相等都是60°.
四条边相等,四个角相等都是90°.
各边相等、各角也相等的多边形是正多边形.如果一个正多边形有n条边,那么这个正多边形叫做正n边形.
矩形是正多边形吗?菱形是正多边形吗?为什么?
矩形不是正多边形，因为四条边不一定相等;
菱形不是正多边形，因为四个角不一定相等.
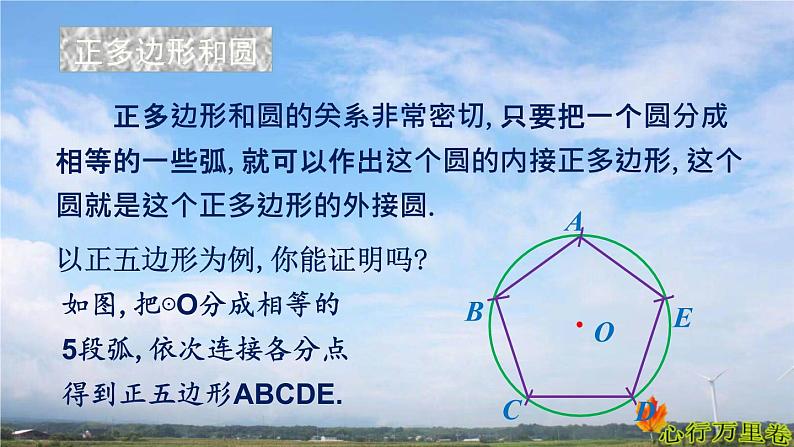
正多边形和圆的关系非常密切,只要把一个圆分成相等的一些弧,就可以作出这个圆的内接正多边形,这个圆就是这个正多边形的外接圆.
以正五边形为例,你能证明吗?
如图,把⊙O分成相等的5段弧,依次连接各分点得到正五边形ABCDE.
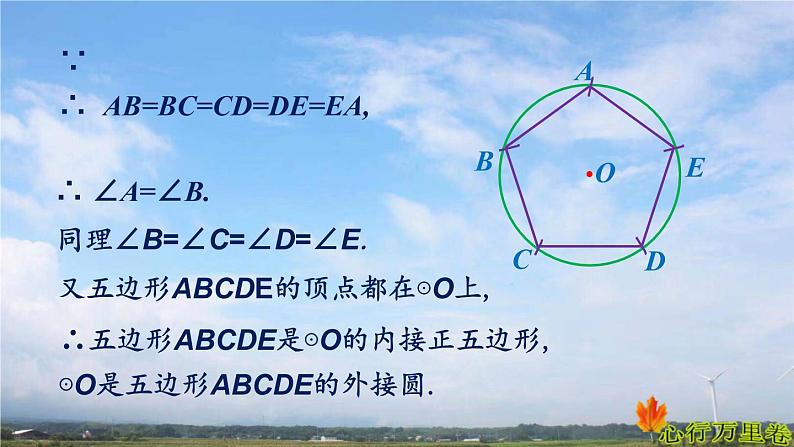
∴ AB=BC=CD=DE=EA,
同理∠B=∠C=∠D=∠E.
又五边形ABCDE的顶点都在⊙O上,
∴五边形ABCDE是⊙O的内接正五边形, ⊙O是五边形ABCDE的外接圆.
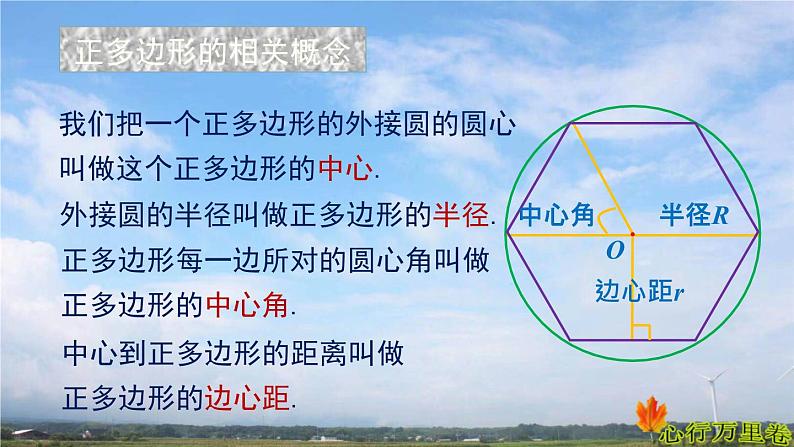
正多边形每一边所对的圆心角叫做正多边形的中心角.
我们把一个正多边形的外接圆的圆心叫做这个正多边形的中心.
外接圆的半径叫做正多边形的半径.
中心到正多边形的距离叫做正多边形的边心距.
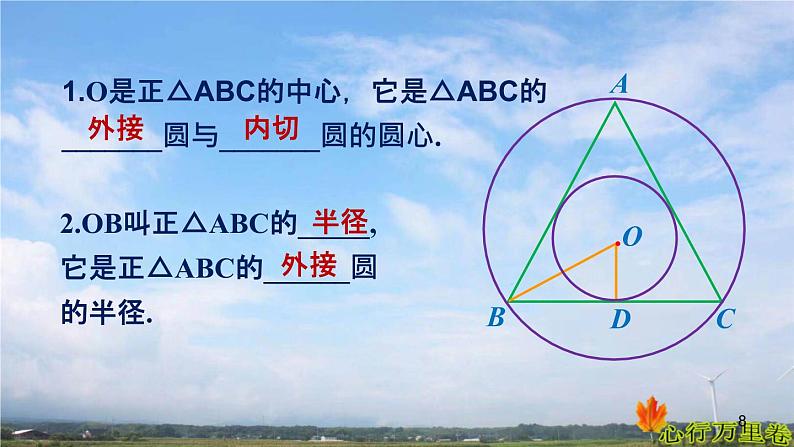
1.O是正△ABC的中心，它是△ABC的_______圆与_______圆的圆心.
2.OB叫正△ABC的_____,它是正△ABC的______圆的半径. 　　　　　
3.OD叫作正△ABC_________, 它是正△ABC的__________圆的半径.
4.∠BOC是正△ABC的________角;
∠BOC=_____度; ∠BOD=_____度.
5.正方形ABCD的外接圆圆心O叫做正方形ABCD的_________.
6.正方形ABCD的内切圆的半径OE叫做正方形ABCD的__________.
7.⊙O是正五边形ABCDE的外接圆，弦AB的弦心距OF叫正五边形ABCDE的________，它是正五边形ABCDE的_______圆的半径.
8.∠AOB叫做正五边形ABCDE的_______角，它的度数是______.
例：有一个亭子它的地基是半径为4 m的正六边形,求地基的周长和面积(结果保留小数点后一位).
利用勾股定理,可得边心距
如图，边心距OG把△AOB分成2个全等的直角三角形.
设正多边形的边长为a,半径为R,它的周长为L=na.
归纳：正多边形的有关计算
由于正多边形在生产、生活实际中有广泛的应用性，所以会画正多边形应是学生必备能力之一.
怎样画一个半径为2cm的正六边形呢？
方法3：如图，以2cm为半径作一个⊙O，由于正六边形的半径等于边长，所以在圆上依次截取等于2cm的弦，就可以将圆六等分，顺次连接各分点即可．
你能尺规作出正八边形吗？
作出⊙O的两条互相垂直的直径，即得圆内接正方形，再过圆心作各边的垂线与⊙O相交，即得圆内接正八边形，
照此方法依次可作正十六边形、正三十二边形、正六十四边形……
方法1：用量角器等分圆周作正n边形. 方法2：用尺规作正方形及由此扩展作正八边形, 用尺规作正六边形及由此扩展作正十二边形．
归纳：作正多边形的方法
提醒：方法1可以画出任意正 n边形.
1.判断.（1）各边都相等的多边形是正多边形. （ ）（2）一个圆有且只有一个内接正多边形. （ ）
2.分别求出半径为R的圆内接正三角形与正方形的边长、周长、边心距和面积.
作等边△ABC的BC边上的高AD,垂足为D.
连接OB，则OB=R .
解：（1）圆内接正三角形
在Rt△OBD中，∠OBD=30°,
连接OB，OC ，作OE⊥BC垂足为E， ∠OEB=90° ∠OBE= ∠ BOE=45°
Rt△OBE为等腰直角三角形，