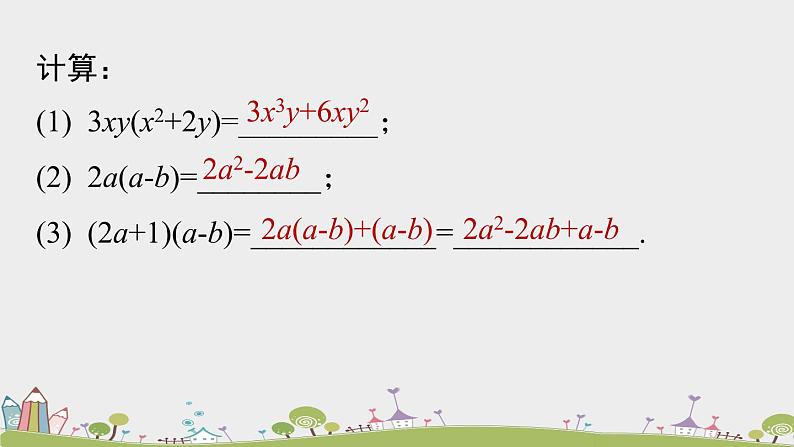
人教版八年级上册14.3.1 提公因式法说课课件ppt

这是一份人教版八年级上册14.3.1 提公因式法说课课件ppt，共28页。PPT课件主要包含了知识回顾，x3y+6xy2，a2-2ab，学习目标，课堂导入，x+1x-1，xx+1，方向相反的变形，因式分解，知识点1因式分解等内容，欢迎下载使用。

p(a+b+c)=pa+pb+pc (p，a，b，c都是单项式).
3.多项式乘以多项式法则：
(a+b)(p+q)=ap+aq+bp+bq (a，b，p，q分别是单项式).
一般地，单项式与单项式相乘把它们的系数、同底数幂分别相乘，对于只在一个单项式里含有的字母，则连同它的指数作为积的一个因式.
2.单项式乘以多项式法则：
1.单项式乘以单项式法则：
计算：(1) 3xy(x2+2y)=_________；(2) 2a(a-b)=________；(3) (2a+1)(a-b)=____________=____________.
2a(a-b)+(a-b)
2a2-2ab+a-b
1.了解并掌握因式分解的定义及意义.2.熟练运用提公因式法进行因式分解.
我们知道，利用整式的乘法运算，有时可以将几个整式的乘积化为一个多项式的形式.反过来，能不能将一个多项式化成几个整式的积的形式呢？若能，这种变形叫做什么呢？这节课，我们一起来讨论这个问题.
请把下列多项式写成整式的乘积的形式：(1) x2+x=________；(2) x2-1=__________.
(1)因为x(x+1)=x(x+1),所以x(x+1) =x(x+1).(2)由平方差公式可知(x+1)(x-1)= x2-1，所以 x2-1= (x+1)(x-1).
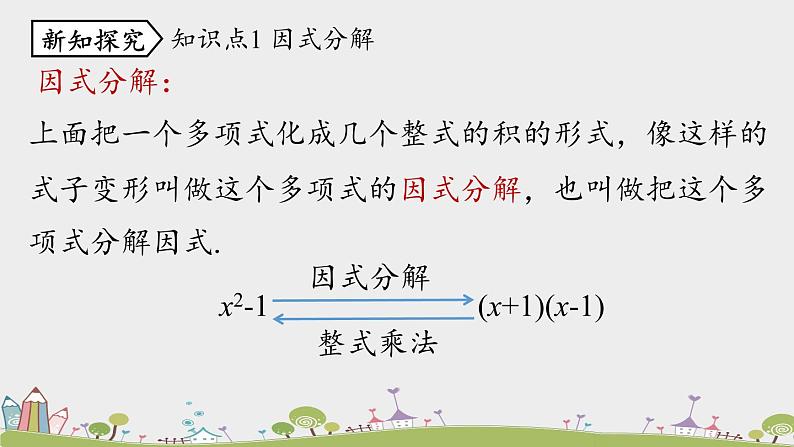
上面把一个多项式化成几个整式的积的形式，像这样的式子变形叫做这个多项式的因式分解，也叫做把这个多项式分解因式.
x2-1 (x+1)(x-1)
(1)因式分解是一种恒等变形，整式乘法是一种运算，故因式分解与整式乘法不是互逆运算，只是方向相反的变形；(2)因式分解不针对单项式，只针对多项式，而且是针对多项式的整体，而不是部分.因式分解的结果中的每个因式都是整式且不能再分解.
例1.下列变形属于因式分解的有（ ）① 8xy3=2xy·4y2 ; ② ; ③ (x+5)(x-5)=x2-25 ;④ x2+2x-3=x(x+2)-3 ; ⑤ x2y+xy2=xy(x+y) .A.4个 B.3个 C.2个 D. 1个
等号的右边不是积的形式
pa + pb +pc
公因式：一个多项式中各项都含有的公共的因式叫做这个多项式各项的公因式.
知识点2 用提公因式法分解因式
取各项系数的最大公约数
可以是单项式，也可以是多项式
取相同字母m中指数最低的m2
取相同字母n中指数最低的n
取2和4的最大公约数2
注意：(1)公因式必须是多项式中各项都含有的公共的因式，只在某一项或某些项中存在而在其他项中没有的因式，不能作为公因式的一部分； (2)公因式可以是数，也可以是单项式或多项式，也可以是多项式的幂的形式；(3)若多项式各项中含有互为相反数的因式，则可将互为相反数的因式统一成相同的因式；若多项式各项中含有相同的多项式因式，则应将其看成一个整体，不要拆开.
为了扩大绿地面积，要把街心花园的一块长p m，宽b m的长方形绿地，向两边分别加宽a m和c m，扩大后的绿地面积是多少？
pa+pb+pc=p(a+b+c)
上面提到的绿地的面积还可以怎样表示？
这样就把pa+pb+pc分解成两个因式乘积的形式，其中一个因式是各项的公因式p，另一个因式a+b+c是pa+pb+pc除以p所得的商.
提公因式法：一般地，如果多项式的各项有公因式，可以把这个公因式提取出来，将多项式写成公因式与另外一个因式的乘积的形式，这种分解因式的方法叫做提公因式法.
用多项式除以公因式，所得的商就是提公因式后剩下的另一个公因式
先确定系数，再确定字母和字母的次数
提公因式法的一般步骤：
例2 把8a3b2+12ab3c分解因式.
取相同字母a中指数最低的a
取相同字母b中指数最低的b2
取8和12的最大公约数4
解：8a3b2+12ab3c=4ab2·2a2+4ab2·3bc=4ab2(2a2+3bc).
按照整式乘法把得到的因式相乘
将得到的结果与原式对比
例3 把2a(b+c)-3(b+c)分解因式.
解：2a(b+c)-3(b+c)=(b+c)(2a-3).
分析：b+c是这两个式子的公因式，可以直接提出.
(1)提公因式法的依据是乘法分配律的逆用，关键是找准公因式；(2)当多项式首项系数是负数时，一般应先提出“-”号，但要注意，此时括号内各项都要改变符号；(3)多项式有几项，提取公因式后，各项的剩余部分组成的新多项式就有几项，不能漏项；(4)当公因式与多项式中某一项相同时，提取公因式后该项剩余的项为“1”，一定不要漏项.
1.判断下列式子中哪些是因式分解？3x+6y=3(x+2y) ;4m2n3+2mn2=2mn2(2mn+1) ;(x+2y)2=x2+4xy+4y2 ;(a+4)(a-4)=a2-16 .
2.（2020·贺州）多项式2a2b3+8a4b2因式分解为（ ）A. a2b2(2b+8a2)B. 2ab2(ab+4a3)C. 2a2b2(b+4a2)D. 2a2b(b2+4a2b)
2a2b2·b+2a2b2·4a2
2a2b2(b+4a2)
3.将下列各式分解因式：(1) ax+ay ; (2) 8mn2+2mn ; (3) 2a(y-z)-3b(z-y) .
解：(1) ax+ay=a(x+y) ;
(2) 8mn2+2mn=2mn(4n+1) ;
(3) 2a(y-z)-3b(z-y)=2a(y-z)+3b(y-z)=(2a+3b)(y-z) .
提公因式并确定另外一个因式
把多项式写成这两个因式的积的形式
解：原式=4a2(x-y)3-2b2(x-y)4 =2(x-y)3[2a2-b2(x-y)] =2(x-y)2(2a2 -b2x+b2y)
1.分解因式： 4a2(x-y)3-2b2(y-x)4.