数学九年级下册第二十八章 锐角三角函数28.2 解直角三角形及其应用教课内容课件ppt

这是一份数学九年级下册第二十八章 锐角三角函数28.2 解直角三角形及其应用教课内容课件ppt，共20页。PPT课件主要包含了学习目标，温故知新，知识点1，在Rt△ABC中，你发现了什么，一角一边，∠A＋∠B＝90°，3边角之间的关系，勾股定理，即学即练等内容，欢迎下载使用。

1．使学生理解直角三角形中五个元素的关系，会运用勾股定理，直角三角形的两个锐角互余及锐角三角函数解直角三角形；2．渗透数形结合的数学思想，培养学生良好的学习习惯.
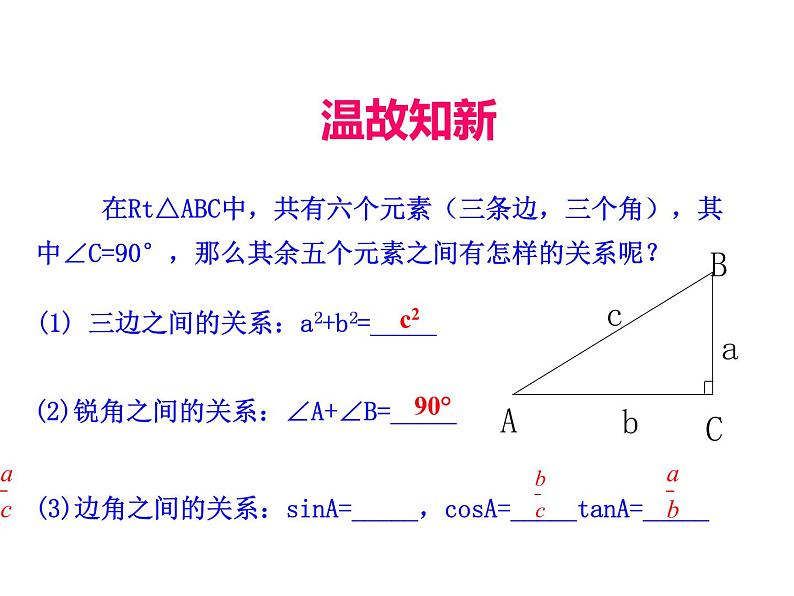
(1) 三边之间的关系：a2+b2=_____
(2)锐角之间的关系：∠A+∠B=_____
(3)边角之间的关系：sinA=_____，csA=_____tanA=_____
在Rt△ABC中，共有六个元素（三条边，三个角），其中∠C=90°，那么其余五个元素之间有怎样的关系呢？
利用计算器可得 .
根据以上条件可以求出塔身中心线与垂直中心线的夹角．你愿意试着计算一下吗？
如图设塔顶中心点为B，塔身中心线与垂直中心线的夹角为A，过B点向垂直中心线引垂线，垂足为点C，在Rt△ABC中，∠C＝90°，BC＝5.2m，AB＝54.5m
将上述问题推广到一般情形，就是：已知直角三角形的斜边和一条直角边，求它的锐角的度数.
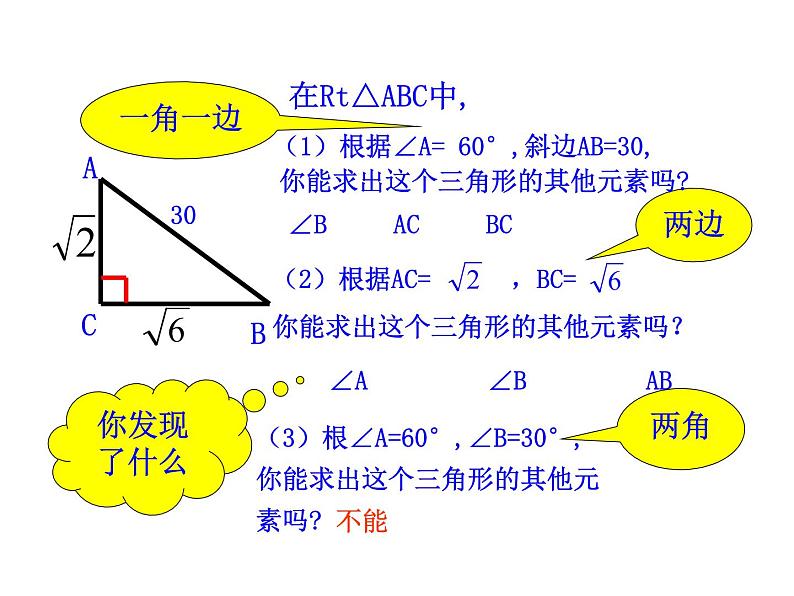
（1）根据∠A= 60°,斜边AB=30,
∠B AC BC
∠A ∠B AB
（3）根∠A=60°,∠B=30°,你能求出这个三角形的其他元 素吗?
你能求出这个三角形的其他元素吗?
在直角三角形的六个元素中,除直角外,如果知道两个元素(其中至少有一个是边),就可以求出其余三个元素.
在直角三角形中,由已知元素求未知元素的过程,叫解直角三角形.
（2）两锐角之间的关系
（1）三边之间的关系
在解直角三角形的过程中，一般要用到下面一些关系：
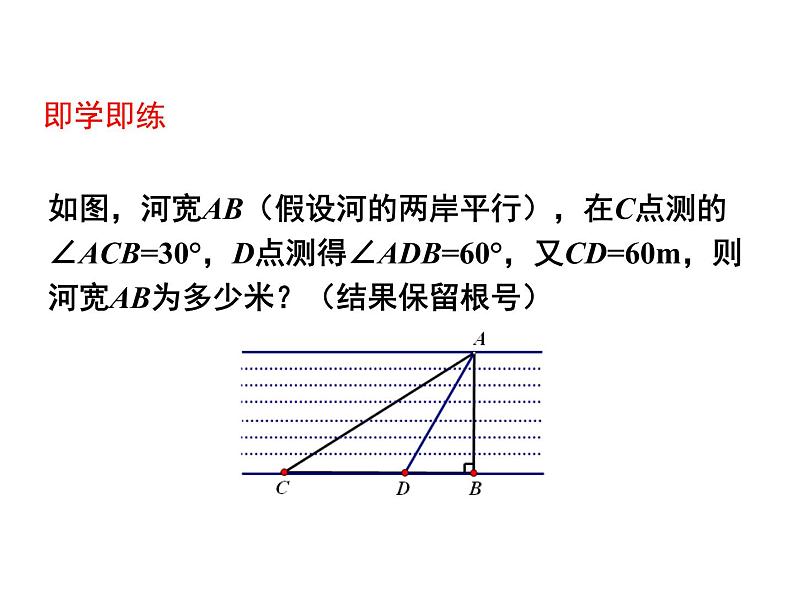
如图，河宽AB（假设河的两岸平行），在C点测的∠ACB=30°，D点测得∠ADB=60°，又CD=60m，则河宽AB为多少米？（结果保留根号）
解：∵∠ACB=30°，∠ADB=60°，
∴∠CAD=30°，AD=CD=60m.
【例1】如图，在Rt△ABC中，∠C＝90°，解这个直角三角形.
【例2】如图，在Rt△ABC中，∠B＝35°，b=20，解这个直角三角形（精确到0.1）
你还有其他方法求出c吗？
1.如图，从点C测得树的顶角为33º，BC＝20米，则树高AB＝________米（用计算器计算，结果精确到0.1米）
AB=BC·tanC=20×tan33°=13.0
1.解直角三角形的关键是找到与已知和未知相关联的直角三角形，当图形中没有直角三角形时，要通过作辅助线构造直角三角形（作某边上的高是常用的辅助线）．2.一些解直角三角形的问题往往与其他知识联系，所以在复习时要形成知识结构，要把解直角三角形作为一种工具，能在解决各种数学问题时合理运用.
1、在下列直角三角形中不能求解的是（ ）(A)已知一直角边一锐角(B)已知一斜边一锐角(C)已知两边(D)已知两角
2. 如图，小明为了测量其所在位置，A点到河对岸B点之间的距离，沿着与AB垂直的方向走了m米，到达点C，测得∠ACB＝α，那么AB等于（ ）(A) m·sinα米 (B) m·tanα米 (C) m·csα米 (D) 米
【解析】一边上的高=6×sin60°=【答案】
4.已知：如图，在Rt△ABC中，∠C＝90°，AC＝ ．点D为BC边上一点，且BD＝2AD，∠ADC＝60°求△ABC的周长（结果保留根号）
【解析】要求△ABC的周长，只要求得BC及AB的长度即可．根据Rt△ADC中∠ADC的正弦值，可以求得AD的长度，也可求得CD的长度；再根据已知条件求得BD的长度，继而求得BC的长度；运用勾股定理可以求得AB的长度，求得△ABC的周长．