初中数学人教版九年级下册28.2 解直角三角形及其应用教学演示课件ppt

这是一份初中数学人教版九年级下册28.2 解直角三角形及其应用教学演示课件ppt，共19页。PPT课件主要包含了情境引入，新知探究，②锐角之间关系，∠A＋∠B＝90°，③边角之间关系，在直角三角形中，例题讲解，巩固提高，总结提升，布置作业等内容，欢迎下载使用。

要想使人安全地攀上斜靠在墙面上的梯子的顶端，梯子与地面所形成的角α一般要满足50°≤ α ≤ 75°，现有一架长6 m的梯子.
（1）使用这架梯子最高可以安全攀上多高的墙（精确到0.1 m）？
（2）当梯子底端距离墙面2.4 m时，梯子与地面 所成的角α等于多少（精确到1°）？这时人是 否能够安全使用 这架梯子？
问题1：上面这个问题（1）可归结为：在Rt△ABC中，∠C=90°，已知∠A=75°，斜边AB=6 m，求BC的长.
分析：角α越大，攀上的高度就越高，所以问题可转化为求 ∠A=75°时BC的长.
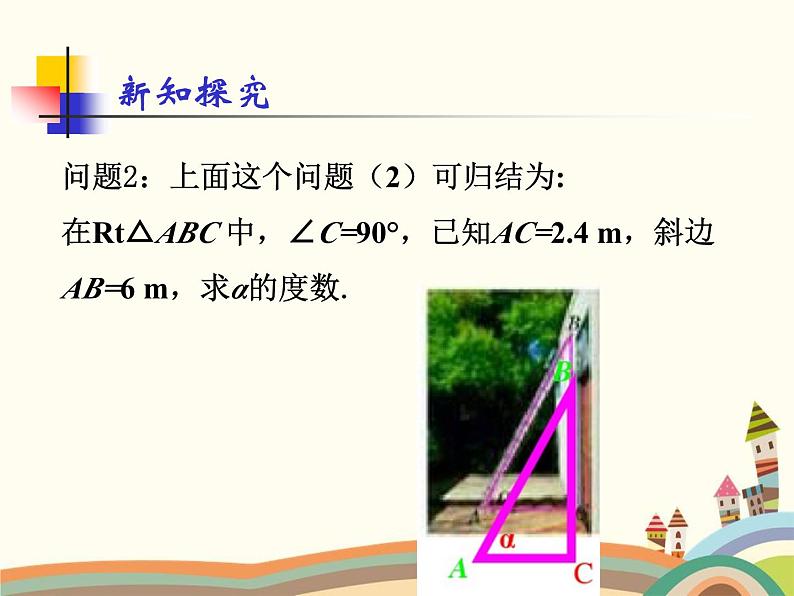
问题2：上面这个问题（2）可归结为:在Rt△ABC 中，∠C=90°，已知AC=2.4 m，斜边AB=6 m，求α的度数.
问题3：在问题（1）（2）中，你还能求出这个直角三角形中的其他元素吗？（边或角的值）
问题4：在此直角三角形中，若∠A=60°，∠B=30°，你能求出此直角三角形中的其他元素吗？
在直角三角形的六个元素中,除直角外的五个元素,只要知道其中的两个元素(至少有一个是边),就可以求出其余三个元素.
在直角三角形中,由已知元素求出未知元素的过程,叫做解直角三角形.
①三边之间关系：
（1）解直角三角形时，只有下面两种情况： ①已知两条边；②已知一条边和一个锐角.
（2）多种方法时的选择原则： ①以简便为原则，尽量用乘不用除，减小计 算量；②尽量用原始数据，减小误差.
1.什么是解直角三角形？2.解直角三角形的知识基础：两锐角互余、 勾股定理、锐角三角函数.
3.方法：（1）在直角三角形的六个元素中，除直角外的五个元素，只要知道其中的两个元素（至少有一个是边），就可以求出其余的三个元素.
（2）解直角三角形时，只有下面两种情况： ①已知两条边； ②已知一条边和一个锐角.
教材第77页习题28.2第1题.