初中数学北师大版九年级上册2 矩形的性质与判定教课ppt课件

这是一份初中数学北师大版九年级上册2 矩形的性质与判定教课ppt课件，共12页。PPT课件主要包含了复习与回顾，矩形的判定，课堂练习，巩固练习等内容，欢迎下载使用。

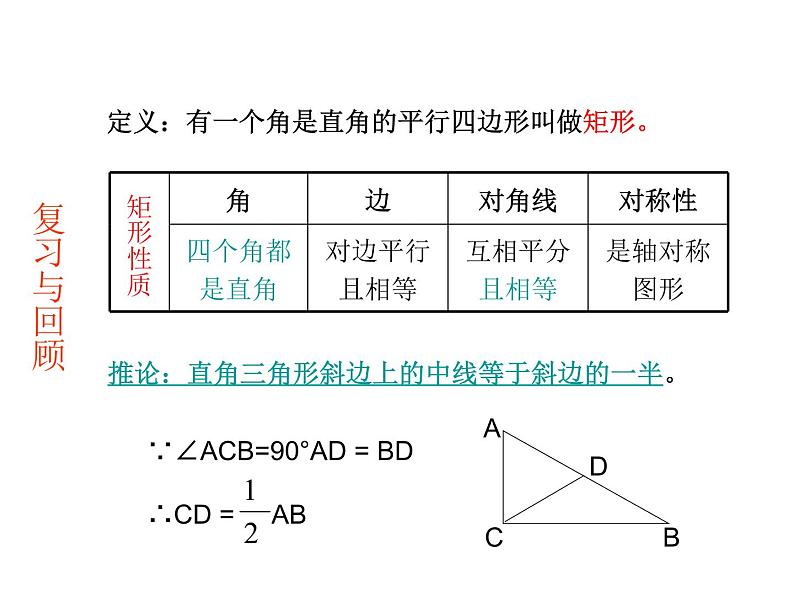
定义：有一个角是直角的平行四边形叫做矩形。
推论：直角三角形斜边上的中线等于斜边的一半。
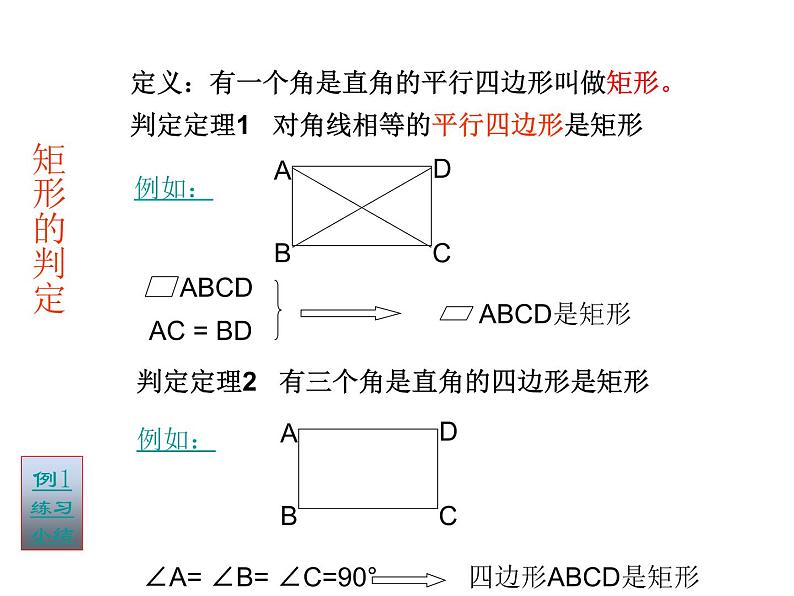
判定定理2 有三个角是直角的四边形是矩形
∠A= ∠B= ∠C=90°
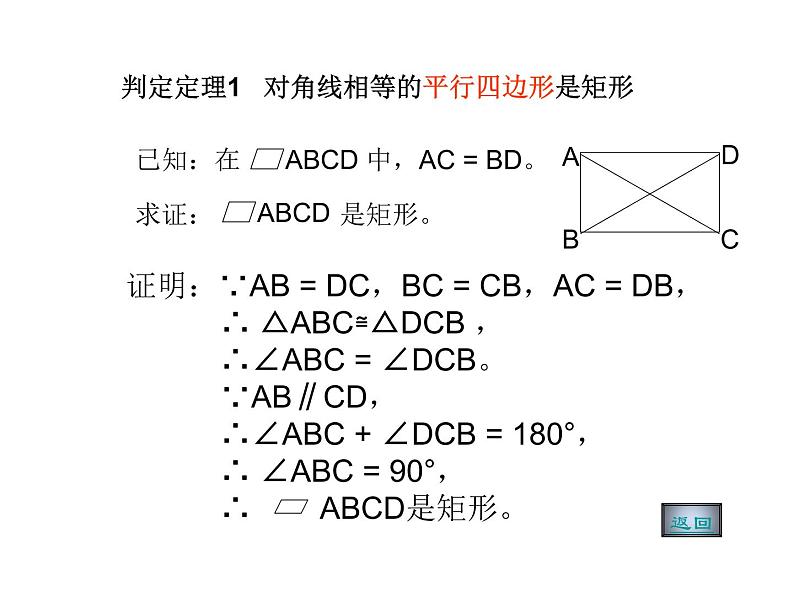
判定定理1 对角线相等的平行四边形是矩形
证明：∵ ∠A= ∠B= ∠C=90°， ∴ ∠A + ∠B = 180°， ∠B + ∠C = 180°， ∴AD∥BC， AB∥DC， ∴四边形ABCD是平行四边形。 ∵ ∠A=90°， ∴四边形ABCD是矩形。
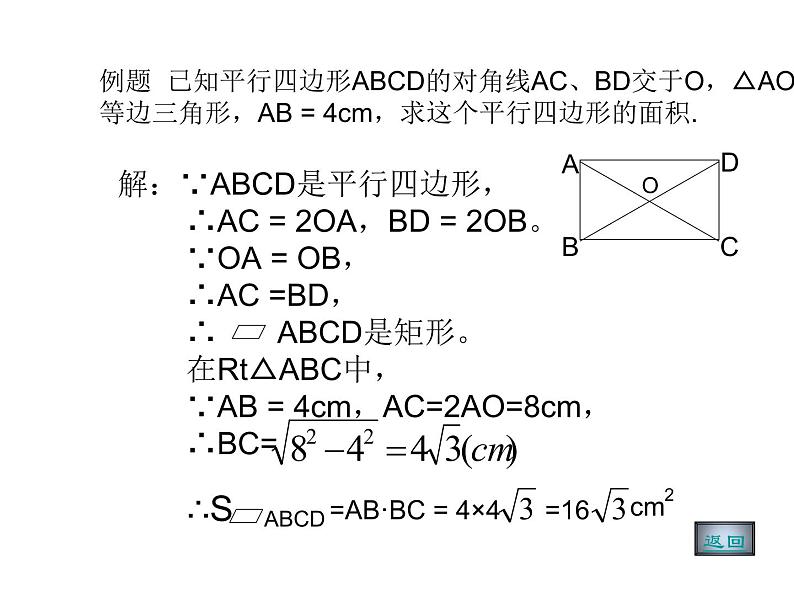
例题 已知平行四边形ABCD的对角线AC、BD交于O，△AOB是等边三角形，AB = 4cm，求这个平行四边形的面积.
1. 对角线相等且一组对边也相等的四边形是矩形． 2. 两条对角线交点到四个顶点距离相等的四边形为矩形． 3. 有一组对边相等，一组对角是直角的四边形是矩形． 4. 有三个角都相等的四边形是矩形．
　5. 具备条件____的四边形是矩形．
A．两条对角线相等 B．对角线互相垂直C．一组对角是直角 D．有三个角是直角
6. 能够判断一个四边形是矩形的条件是
　A．对角线相等 B．对角线垂直　C．对角线互相平分且相等 D．对角线垂直且相等
如图，在平行四边形ABCD中，AC与BD 交于O，如图，①若∠1=∠2，则平行四边形ABCD是矩形吗？为什么？②若△AOB是正三角形，则平行四边形ABCD是矩形是矩形吗？为什么？
1.已知：矩形ABCD的两条对角线相交于点O，∠AOD= 120°，AB=4cm，求矩形对角线的长。
2.已知平行四边形ABCD的对角线AC和BD相交于 点O，△AOB是等边三角形，AB＝ 4 cm。求这 个平行四边形的面积。
3.已知:如图,平行四边形ABCD的四个内角平分线相交于点E，F， G，H。求证：EG＝FH。
4.已知:如图,在△ABC中,∠C＝ 90°,CD为中线, 延长CD到点E,使得 DE＝CD。连结AE，BE， 则四边形ACBE为矩形。
矩形的判定方法分两类： 从四边形来判定和从平行四边形来判定．
常用的判定方法有三种： 定义和两个判定定理．遇到具体题目， 可根据条件灵活选用恰当的方法．