初中数学人教版九年级上册21.3 实际问题与一元二次方程精品课件ppt

这是一份初中数学人教版九年级上册21.3 实际问题与一元二次方程精品课件ppt，共19页。PPT课件主要包含了审清题意，设未知数，列方程，解方程验根，知识回顾，学习目标，课堂导入，1+x，1-x，1-x2等内容，欢迎下载使用。

列一元二次方程解决实际问题的一般步骤：
1.能通过构建一元二次方程模型解决增长率与降低率问题.
2.用一元二次方程模型解实际问题.
思考,并填空：1.某户的粮食产量年平均增长率为x,第一年的产量为60000kg,第二年的产量为___________kg,第三年的产量___________kg.2.前年生产1吨甲种药品的成本是5000元,随着生产技术的进步,成本下降,设年平均下降率是x,则去年生产1吨甲种药品的成本是 元,如果保持这个下降率,则现在生产1吨甲种药品的成本是 元.
60000(1+x)2
你能归纳上述两个问题中蕴含的等量关系吗？
两年后：变化前的量a×(1±x)2=变化后的量b
x为平均增长(或降低)百分率,a是增长(或降低)前的量,b是增长(或降低)2次后的量,其中增长取“+”,降低取“－”.
“变化率”问题公式：a(1±x)2=b
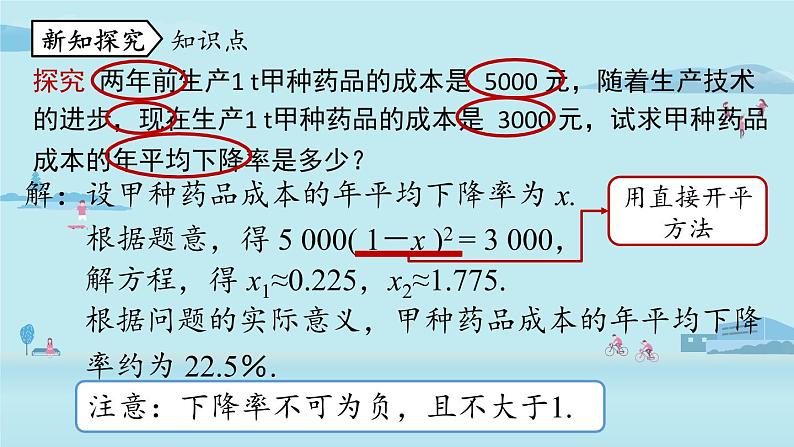
探究 两年前生产1 t甲种药品的成本是 5000 元，随着生产技术的进步，现在生产1 t甲种药品的成本是 3000 元，试求甲种药品成本的年平均下降率是多少？
解：设甲种药品成本的年平均下降率为 x. 根据题意，得
5 000( 1－x )2 = 3 000，
x1≈0.225，x2≈1.775.
根据问题的实际意义，甲种药品成本的年平均下降率约为 22.5％.
注意：下降率不可为负，且不大于1.
两年前生产 1 t乙种药品的成本是 6000 元，随着生产技术的进步，现在生产 1 t乙种药品的成本是 3600 元，试求乙种药品成本的年平均下降率是多少？
解：设乙种药品成本的年平均下降率为 y. 根据题意，得
6 000 ( 1－y )2 = 3 600.
y1≈0.225，y2≈1.775.
根据问题的实际意义，乙种药品成本的年平均下降率约为 22.5％.
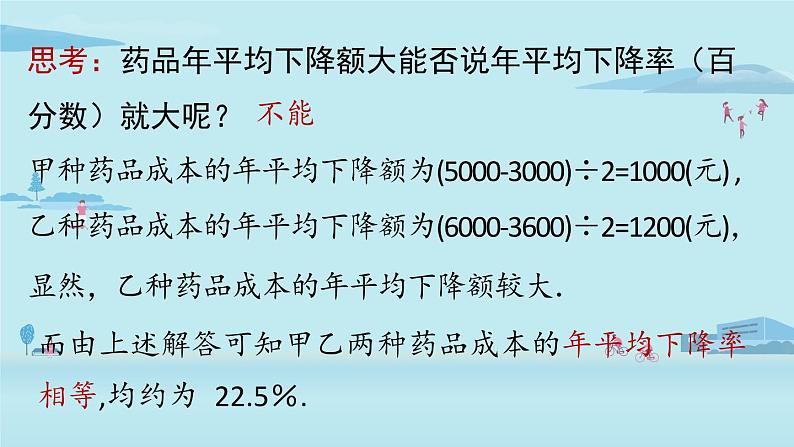
甲种药品成本的年平均下降额为(5000-3000)÷2=1000(元) , 乙种药品成本的年平均下降额为(6000-3600)÷2=1200(元)，显然，乙种药品成本的年平均下降额较大．
思考：药品年平均下降额大能否说年平均下降率（百分数）就大呢？
而由上述解答可知甲乙两种药品成本的年平均下降率相等,均约为 22.5％.
你能总结出有关增长率和降低率的数量关系吗？
类似这种增长率的问题在实际生活中普遍存在，有一定的模式．
增长(或降低)前的量是 a
增长(或降低) n 次后的量是 b
平均增长(或降低)百分率为 x
增长取“+”，降低取“－”
例1 某厂今年一月份的总产量为500吨,三月份的总产量为720吨,平均每月增长率是x,列方程( ) A.500(1+2x)=720 B.500(1+x)2=720 C.500(1+x2 )=720 D.720(1+x)2=500
例2 某市从 2020 年开始大力发展旅游产业.据统计，该市2020年旅游收入约为2亿元，预计2022年旅游收入达到2.88亿元，据此估计该市2021年、2022年旅游收入的年平均增长率约为( )
A.2% B.4.4% C.20% D.44%
解：设该市2021年、2022年旅游收入年平均增长率为 x.根据题意，得2(1+x)2=2.88，解方程，得x1=0.2=20%，x2=-2.2(不合题意，舍去)，所以该市2021年、2022年旅游收入的年平均增长率约为20%.
解：设这个增长率为x. 根据题意，得200+200(1+x)+200(1+x)2=950 ， 整理方程，得4x2+12x-7=0， 解这个方程，得x1=-3.5(舍去),x2=0.5. 答：这个增长率为50%.
例3 某公司去年的各项经营中,一月份的营业额为200万元,一月、二月、三月的营业额共950万元,如果平均每月营业额的增长率相同,求这个增长率．
1.在园林化城市建设期间，某市2018年绿化面积约为1000万平方米，2020年绿化面积约为1210万平方米．如果近几年绿化面积的年增长率相同，则2021年绿化面积约为（　　） A. 1221万平方米 B. 1331万平方米 C. 1231万平方米 D. 1323万平方米
解：设每年绿化面积的平均增长率为x．根据题意，得1000(1+x)2=1210．解方程，得x1=0.1=10%，x2=-2.1(不合题意，舍去)．所以每年绿化面积的平均增长率为10%．故2021年绿化面积约为1210×(1+10%)=1331(万平方米).
2.某商品现在的售价为每件60元，每星期可卖出300件，市场调查反映：销售单价每降低1元，每星期可多卖出20件，已知商品的进价为每件40元，在顾客得实惠的前提下，商家每星期还想获得6080元的利润，应将销售单价定为多少元？
解：设商品的销售单价应降低 x 元，则商品的销售单价为(60-x)元，销售量为(300+20x)件.列方程，得 (60-x-40)(300+20x)=6080，整理，得x2-5x+4=0，解方程，得x1=1，x2=4，要使顾客得实惠，取 x=4，所以销售单价定为 56 元.答：应将销售单价定为 56 元.
a(1+x)2=b，其中 a 为增长前的量，x 为增长率，2 为增长次数，b 为增长后的量.
a(1-x)2=b，其中 a 为降低前的量，x 为降低率，2 为降低次数，b 为降低后的量.注意 1 与 x 位置不可调换.
解：(1)设2019年到2021年该品牌足球单价平均每年降低的百分率为 x，根据题意得 200×(1-x)2=162，解得x1=0.1=10%，x2=1.9(不符合题意，舍去)，答： 2019年到2020年该品牌足球单价平均每年降低的百分率为10%.
(1)求2019年到2021年该品牌足球单价平均每年降低的百分率.
1.某中学开设了“足球大课间”活动，现需要购进100个某品牌的足球供学生使用.经调查，该品牌足球2019年单价为200元，2021年单价为162元.
(2)2021年选购期间发现该品牌足球在两个文体用品商场有不同的促销方案： ①A 商场买十送一；②B 商场全场九折. 试问去哪个商场购买足球更优惠?
解：A商场买10个送1个，买90个送9个，共计99个，我们只需要购买91个，再加上送的9个就是100个.因此在A商场我们买100个球的费用是91×162=14742元.
B商场打九折，即每个球的单价为162×0.9=145.8元，购买100个费用为100×145.8=14580<14742.故在B商场购买更便宜.
解：(1)设该地投入异地安置资金的年平均增长率为 x ，根据题意，得 1 280(1+x)2=1 280+1 600，解得x1=0.5=50%，x2=-2.5(舍去)，答：从2019年到2021年，该地投入异地安置资金的年平均增长率为50%.
(1)从2019年到2021年，该地投入异地安置资金的年平均增长率为多少？
2.某地2019年为做好“精准扶贫”，投入资金1 280万元用于异地安置，并规划投入资金逐年增加，2021年在2019年的基础上增加投入资金1 600万元.