人教版九年级下册第二十六章 反比例函数综合与测试单元测试课后测评

人教版数学九年级下册

《反比例函数》单元测试题

一、选择题

1.如果直角三角形的面积一定，那么下列关于这个直角三角形边的关系中，正确的是(        )

A．两条直角边成正比例             B．两条直角边成反比例

C．一条直角边与斜边成正比例       D．一条直角边与斜边成反比例

2.已知y与x-1成反比例，那么它的解析式为(      )

3.若点M（﹣3，a），N（4，﹣6）在同一个反比例函数的图象上，则a的值为（      ）

   A.8                   B.﹣8                 C.﹣7                    D.5

4.有一个装有水的容器，如图所示.容器内的水面高度是10cm，现向容器内注水，并同时开始计时，在注水过程中，水面高度以每秒0.2cm的速度匀速增加，则容器注满水之前，容器内的水面高度与对应的注水时间满足的函数关系是（    ）

A.正比例函数关系  B.一次函数关系   C.二次函数关系   D.反比例函数关系

5.已知一个函数关系满足下表(x为自变量)，则这个函数解析式是(     ).

6.如果反比例函数的图象经过点(-1，-2)，那么k的值是（   ）

A.2       B.-2         C.-3         D.3

7.若双曲线y=位于第二、四象限，则k的取值范围是(　　)

A.k＜1            B.k≥1           C.k＞1            D.k≠1

8.如图，函数y=kx＋b(k≠0)与y=(m≠0)的图象相交于点A(2，3)，B(-6，-1)，则不等式kx＋b＞的解集为(　　)

A.x＜-6       B.-6＜x＜0或x＞2       C.x＞2        D.x＜-6或0＜x＜2

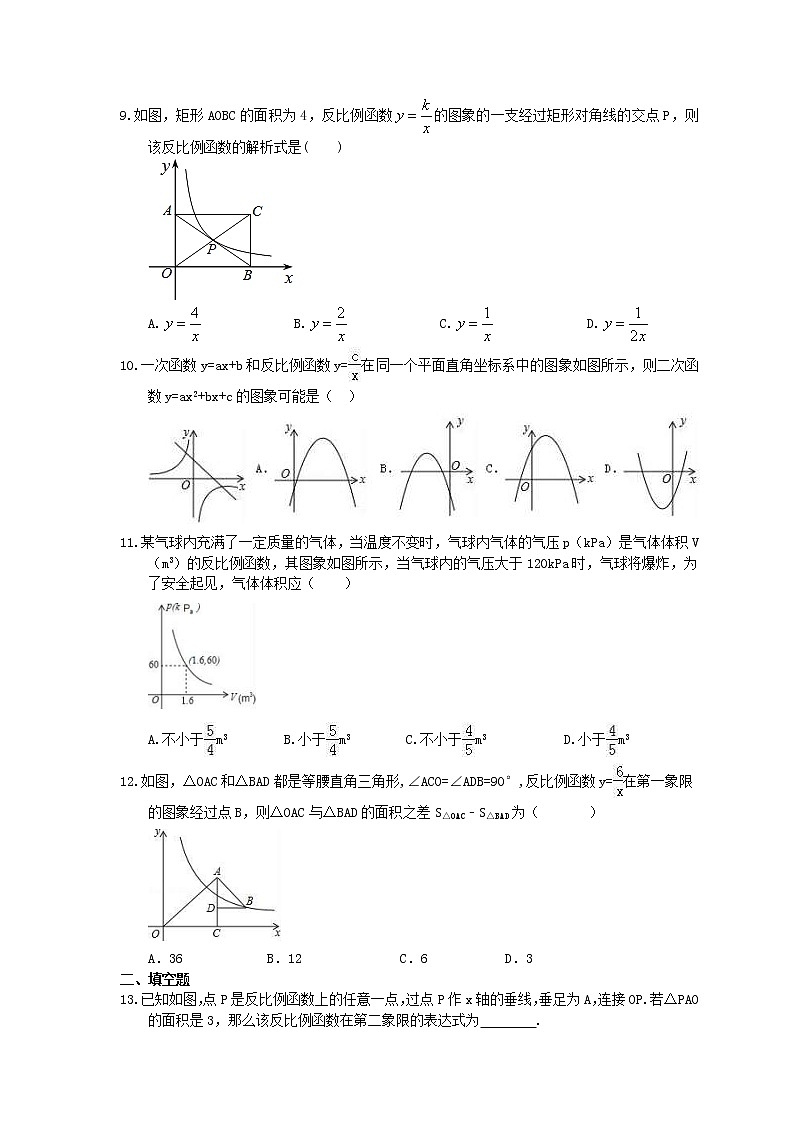
9.如图，矩形AOBC的面积为4，反比例函数的图象的一支经过矩形对角线的交点P，则该反比例函数的解析式是(　　)

A.        B.        C.       D.

10.一次函数y=ax+b和反比例函数y=在同一个平面直角坐标系中的图象如图所示，则二次函数y=ax2+bx+c的图象可能是（  ）

11.某气球内充满了一定质量的气体，当温度不变时，气球内气体的气压p（kPa）是气体体积V（m3）的反比例函数，其图象如图所示，当气球内的气压大于120kPa时，气球将爆炸，为了安全起见，气体体积应（　　）

A.不小于m3                      B.小于m3                      C.不小于m3                         D.小于m3

12.如图，△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y=在第一象限的图象经过点B，则△OAC与△BAD的面积之差S△OAC﹣S△BAD为（       ）

A．36                          B．12                            C．6                         D．3

二、填空题

13.已知如图，点P是反比例函数上的任意一点，过点P作x轴的垂线，垂足为A，连接OP.若△PAO的面积是3，那么该反比例函数在第二象限的表达式为        .

14.如图,在平面直角坐标系中,直线l∥x轴,且直线l分别与反比例函数y=(x>0)和y=﹣(x<0)的图象交于点P、Q,连结PO、QO,则△POQ的面积为     ．

15.在函数y=（k为常数）的图象上有三个点（﹣2，y1），（﹣1，y2），（0.5，y3），函数值y1，y2，y3的大小为　　　　　　．

16.如图,等腰Rt△ABC的斜边BC在x轴上,顶点A在反比例函数的图象上,连接OA,若OB=2,则点A的坐标为       ．

17.李老师参加了某电脑公司推出的分期付款(无利息)购买电脑活动，他购买的电脑价格为9800元，交了首付之后每月付款y元，x个月结清余款，y与x满足如图的函数解析式，通过以上信息可知李老师的首付款为________.

18.如图，点A为函数y=（x＞0）图象上一点，连结OA，交函数y=（x＞0）的图象于点B，点C是x轴上一点，且AO=AC，则△ABC的面积为     ．

三、解答题

19.已知y=y1+y2,y1与x2成正比例，y2与x+3成反比例。并且x=0时，y=2，x=1时，y=0.

   试求函数y的解析式，并指出自变量的取值范围。

20.已知一次函数y=-x-1与反比例函数y=kx-1的图象都过点A（m，1）.

（1）求m的值，并求反比例函数的解析式；

（2）求正比例函数与反比例函数的另一个交点B的坐标；

（3）求△AOB的面积。

21.如图，已知一次函数y1=x+m（m为常数）的图象与反比例函数y2=（k为常数，k≠0）的图象相交于点A（1，3）、B（﹣3，n）.

（1）求这两个函数的解析式及其图象的另一交点B的坐标；

（2）观察图象，写出使函数值0＞y1≥y2的自变量x的取值范围.

22.如图,在平面直径坐标系中,反比例函数y=（x＞0）的图象上有一点A（m,4）,过点A作AB⊥x轴于点B,将点B向右平移2个单位长度得到点C,过点C作y轴的平行线交反比例函数的图象于点D,CD=.

（1）点D的横坐标为        （用含m的式子表示）；

（2）求反比例函数的解析式．

23.近年来，我国煤矿安全事故频频发生，其中危害最大的是瓦斯，其主要成分是CO.在一次矿难事件的调查中发现：从零时起，井内空气中CO的浓度达到4 mg/L，此后浓度呈直线型增加，在第7小时达到最高值46 mg/L，发生爆炸；爆炸后，空气中的CO浓度成反比例下降.如图，根据题中相关信息回答下列问题：

（1）求爆炸前后空气中CO浓度y与时间x的函数关系式，并写出相应的自变量取值范围；

（2）当空气中的CO浓度达到34 mg/L时，井下3 km的矿工接到自动报警信号，这时他们至少要以多少km/h的速度撤离才能在爆炸前逃生？

（3）矿工只有在空气中的CO浓度降到4 mg/L及以下时，才能回到矿井开展生产自救，求矿工至少在爆炸后多少小时才能下井?

24.如图，一次函数y1=k1x+2与反比例函数的图象交于点A(4，m）和B(﹣8，﹣2），与y轴交于点C．

(1）k1=　   　，k2=　   　；

(2）根据函数图象可知，当y1＞y2时，x的取值范围是　   　；

(3）过点A作AD⊥x轴于点D，点P是反比例函数在第一象限的图象上一点．设直线OP与线段AD交于点E，当S四边形ODAC：S△ODE=3：1时，求点P的坐标．

25.如图，直线y1=﹣x+4，y2=x+b都与双曲线y=交于点A(1，m），这两条直线分别与x轴交于B，C两点．

(1）求y与x之间的函数关系式；

(2）直接写出当x＞0时，不等式x+b＞的解集；

(3）若点P在x轴上，连接AP把△ABC的面积分成1：3两部分，求此时点P的坐标．

0.参考答案

1.B

2.C

3.A

4.答案为：B

5.答案为：C

6.答案为：D.

7.答案为：A；　

8.B

9.答案为：C；

10.A

11.C.

12.D

13.答案为：y=﹣(x＜0).

14.答案为7．

15.答案为：y3＜y1＜y2．

16.答案为：（3，1）．

17.答案为：3800元

18.答案为：6．

19.解:

20.答案：(1)m=-2,y=2x-1；(2)B(1,-2)；

(3)直线AB解析式为y=-x-1,与y轴交点坐标C（-1,0）∴S△AOB=S△AOC+S△BOC=1.5.

21.解：（1）将点A（1，3）代入反比例函数y2=得：3=，解得：k=3，

所以反比例函数表达式为：y2=；将点A代入一次函数y1=x+m得：3=1+m，解得：m=2，

所以一次函数表达式为：y1=x+2；

将B（﹣3，n）代入反比例函数y2=得：n==﹣1，所以点B的坐标为：（﹣3，﹣1）.

（2）∵y1=x+2，令y=0，则0=x+2，x=﹣2，∴直线AB与x轴的交点为（﹣2，0），

∵B（﹣3，﹣1），∴使函数值0＞y1≥y2的自变量x的取值范围是﹣3≤x＜﹣2.

22.解：（1）∵A（m，4），AB⊥x轴于点B，∴B的坐标为（m，0），

∵将点B向右平移2个单位长度得到点C，∴点C的坐标为：（m+2，0），

∵CD∥y轴，∴点D的横坐标为：m+2；故答案为：m+2；

（2）∵CD∥y轴，CD=，∴点D的坐标为：（m+2，），

∵A，D在反比例函数y=（x＞0）的图象上，∴4m=（m+2），解得：m=1，

∴点a的横坐标为（1，4），∴k=4m=4，∴反比例函数的解析式为：y=．

23.解：（1）因为爆炸前浓度呈直线型增加，

所以可设y与x的函数关系式为

由图象知过点（0，4）与（7，46）

∴.              解得,

∴,此时自变量的取值范围是0≤≤7.

因为爆炸后浓度成反比例下降，所以可设y与x的函数关系式为.[

由图象知过点（7,46），∴.    ∴,

∴，此时自变量的取值范围是＞7.

（2）当=34时，由得,6+4=34，=5 .

∴撤离的最长时间为7-5=2(小时).

∴撤离的最小速度为3÷2=1.5(km/h).

 (3)当y=4时，由得,x=80.5，80.5-7=73.5(小时).

∴矿工至少在爆炸后73.5小时能才下井.

24.解：(1）∵一次函数y1=k1x+2与反比例函数的图象交于点A(4，m）和B(﹣8，﹣2），

∴K2=(﹣8）×(﹣2）=16﹣2=﹣8k1+2∴k1=

(2）∵一次函数y1=k1x+2与反比例函数的图象交于点A(4，4）和B(﹣8，﹣2），

∴当y1＞y2时，x的取值范围是﹣8＜x＜0或x＞4；

(3）由(1）知，．

∴m=4，点C的坐标是(0，2）点A的坐标是(4，4）．∴CO=2，AD=OD=4．

∴．

∵S梯形ODAC：S△ODE=3：1，∴S△ODE=S梯形ODAC=×12=4，即OD•DE=4，

∴DE=2．∴点E的坐标为(4，2）．

又点E在直线OP上，∴直线OP的解析式是．

∴直线OP与 的图象在第一象限内的交点P的坐标为( ）．

故答案为：，16，﹣8＜x＜0或x＞4

25.解：

(1）把A(1，m）代入y1=﹣x+4，可得m=﹣1+4=3，∴A(1，3），

把A(1，3）代入双曲线y=，可得k=1×3=3，

∴y与x之间的函数关系式为：y=；

(2）∵A(1，3），∴当x＞0时，不等式x+b＞的解集为：x＞1；

(3）y1=﹣x+4，令y=0，则x=4，∴点B的坐标为(4，0），

把A(1，3）代入y2=x+b，可得3=+b，∴b=，∴y2=x+，

令y=0，则x=﹣3，即C(﹣3，0），∴BC=7，

∵AP把△ABC的面积分成1：3两部分，

∴CP=BC=，或BP=BC=，∴OP=3﹣=，或OP=4﹣=，

∴P(﹣，0）或(，0）．