




数学沪科版18.2 勾股定理的逆定理示范课ppt课件
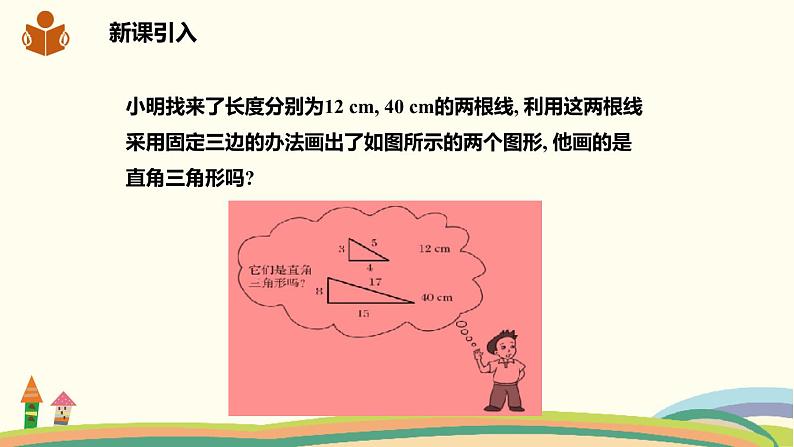
展开小明找来了长度分别为12 cm, 40 cm的两根线, 利用这两根线采用固定三边的办法画出了如图所示的两个图形, 他画的是直角三角形吗?
(1)分别以5,12,13; 3,4,5; 8,15,17; 7,24,25为三边长作三角形, 用量角器量一量, 它们都是直角三角形吗?
(2)如果每组数中三边的长度分别是a, b, c, 那么它们满足a2+b2=c2 吗?
(3)根据(1)(2)你能总结出怎样的结论?
如果三角形的三边长a, b, c满足a2+b2=c2, 那么这个三角形是直角三角形.
(4)勾股定理和其逆定理有什么区别?
勾股数的注意事项:①符合a2+b2=c2;②必须是正整数.
(5)勾股数的定义 满足a2+b2=c2的三个正整数, 称为勾股数.
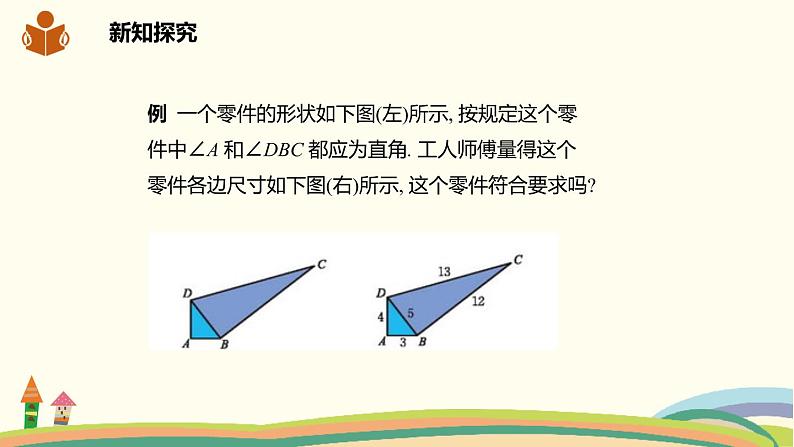
例 一个零件的形状如下图(左)所示, 按规定这个零件中∠A 和∠DBC 都应为直角. 工人师傅量得这个零件各边尺寸如下图(右)所示, 这个零件符合要求吗?
解: 在△ABD中, AB2+AD2=9+16=25=BD2, 所以△ABD是直角三角形, ∠A是直角.在△BCD中, BD2+BC2=25+144=169=CD2, 所以△BCD是直角三角形, ∠DBC是直角.因此, 这个零件符合要求.
〔解析〕如果三角形三边之间的关系存在着 a2+b2=c2, 那 么就可以判定是直角三角形.
1.勾股定理与其逆定理的关系: 勾股定理是已知直角三角形, 得到三边长的关系, 它是直角三角形的重要性质之一;而勾股定理的逆定理是由三角形三边长的关系判断一个三角形是不是直角三角形, 这是直角三角形的判定, 也是判断两直线是否垂直的方法之一, 二者的条件和结论刚好相反.
2.勾股定理的逆定理的延伸: 如果三角形的三边长 a, b, c 满足 a2+b2=c2, 那么这个三角形是直角三角形; 如果 a2+b2
3.勾股定理的逆定理的应用: 应用勾股定理的逆定理可以判断一个三角形是不是直角三角形, 在实际应用时, 可用较短两边长的平方和与较长边长的平方作比较, 若它们正好相等, 则三角形为直角三角形,较长边所对的角为直角.
1.以下各组数为三边长的三角形中, 能组成直角三角形的是( )A.3,4,6 B.9,12,15C.5,12,14 D.10,16,25
解析: A.32+42≠62, 故不是直角三角形, 故不正确; B.92+122=152,故是直角三角形, 故正确; C.52+122≠142, 故不是直角三角形, 故不正确; D.102+162≠252, 故不是直角三角形, 故不正确. 故选B.
2.△ABC的三边长分别为a, b, c, 在下列条件下, 不能判定△ABC是直角三角形的是 ( )A.a2 = b2-c2 B.a2:b2:c2 = 1:2:3C.∠A=∠B-∠CD.∠A:∠B:∠C = 3:4:5
如果三角形的三边长a, b, c满足 a2+b2=c2, 那么这个三角形是直角三角形.
勾股定理的逆定理的应用: 应用勾股定理的逆定理可以判断一个三角形是不是直角三角形, 在实际应用时, 可用较短两边长的平方和与较长边长的平方作比较, 若它们正好相等, 则三角形为直角三角形, 较长边所对的角为直角.
解析: ∵AB2+BC2=32+42=25=52=AC2, ∴△ABC是直角三角形. ∵AC2+CD2=52+122=132=AD2, ∴△ACD也是直角三角形,∴S四边形ABCD= AB·BC+ AC·CD= ×3×4+ ×5×12=36. 故选B.
1.如图所示, 四边形ABCD中, AB=3, BC=4, AC=5, CD=12, AD=13,则四边形ABCD的面积为( )A.72 B.36 C.66 D.42
初中18.2 勾股定理的逆定理集体备课课件ppt: 这是一份初中18.2 勾股定理的逆定理集体备课课件ppt,共13页。PPT课件主要包含了做一做,∠C是直角吗,作业做课后练习等内容,欢迎下载使用。
沪科版八年级下册18.2 勾股定理的逆定理教案配套课件ppt: 这是一份沪科版八年级下册18.2 勾股定理的逆定理教案配套课件ppt,共13页。PPT课件主要包含了想一想,∠C是90°,动手画一画,古埃及人的探究,勾股定理的逆命题,勾股定理,逆命题,例题讲解,∴a2+b2=c2,∴b2+c2≠a2等内容,欢迎下载使用。
沪科版八年级下册18.2 勾股定理的逆定理背景图课件ppt: 这是一份沪科版八年级下册18.2 勾股定理的逆定理背景图课件ppt,共17页。PPT课件主要包含了问题情境,实践探究,互逆命题,小游戏,综合运用,小结梳理等内容,欢迎下载使用。













