






初中数学沪科版八年级下册18.2 勾股定理的逆定理课文配套ppt课件
展开问题1:请用文字叙述勾股定理?
直角三角形的两条直角边的平方和等于第三边的平方.
问题2:你能说出上述定理的逆命题吗?它是真命题吗?
逆命题:如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形.
1.据说,几千年前的古埃及人就已知知道,在一根绳子上连续打上等距离的13个结,然后,用钉子将第1个与第13个结钉在一起,拉紧绳子,再在第4个和第8个结处各钉上一个钉子,如图所示,这样围成的三角形中,最长边所对的角就是直角.
2.用圆规、直尺作△ABC,使AB=5, AC=4,BC=3,如图所示,量一量 ∠C,它是90°吗?
为什么用上面三条线段围成的三角形,就一定是直角三角形呢?你能说明理由吗?
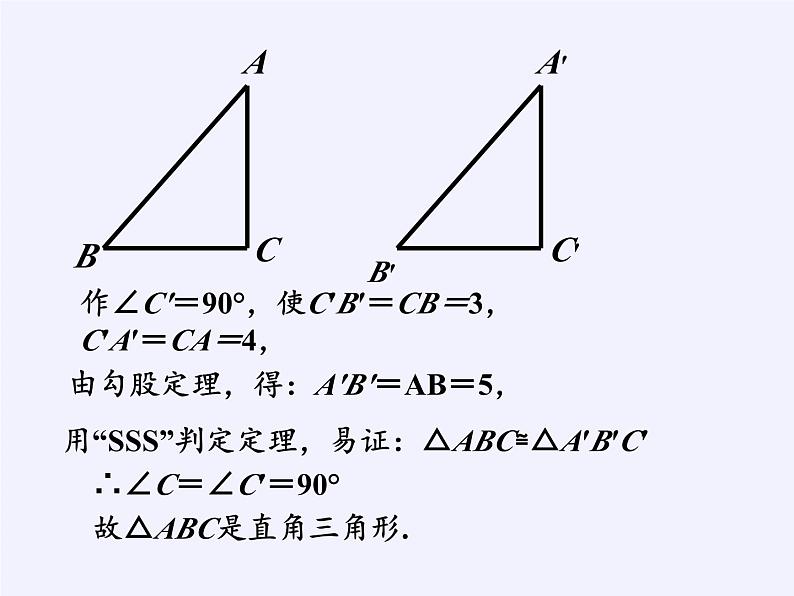
作∠C′=90°,使C′B′=CB=3,C′A′=CA=4,
用“SSS”判定定理,易证:△ABC≌△A′B′C′
∴∠C=∠C′=90°
故△ABC是直角三角形.
由勾股定理,得:A′B′=AB=5,
思考: 在△ABC中,AB=5,AC=4,BC=3,这三条线段之间有何数量关系呢?
即: BC2+AC2=AB2
勾股定理的逆定理:如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形.
设在△ABC中,AB=a,AC=b,BC=c,
如果这三边有下列关系:
那么△ABC是直角三角形,且∠C=90°.
例1 根据下列三角形的三边a,b,c的值,判断△ABC是不是直角三角形,如果是,指出哪条边所对的角是直角.
(1)a=7,b=24,c=25;
解:(1) ∵最大边是c=25,c2=625, a2+b2=72+242=625,
∴ △ABC是直角三角形,最大边c所对角是直角.
(2)a=7,b=8,c=11;
解:(2) ∵最大边是c=11,c2=121, a2+b2=72+82=113,
∴ △ABC不是直角三角形.
勾股数:能够成为直角三角形三条边长度的三个正整数,称为勾股数.
像上面的7、24、25这三个数,我们称之为勾股数.
1.判断下列三边组成的三角形是不是直角三角形:(1)a=2,b=3,c=4. ( )(2)a=9,b=7,c=12. ( )(3)a=25,b=20,c=15.( )
152+202=252
2.三角形三边a,b,c满足条件:
(a+b)2-c2=2ab,此三角形是( )
3.一组勾股数的2倍一定是勾股数吗? 为什么?
解:设这组勾股数为a,b,c,其中c是最大边,
则:a2+b2=c2,
这组数乘以2后,所得新的一组数分别为:2a,2b,2c,
∵(2a)2+(2b)2=4(a2+b2)=4c2,
∴(2a)2+(2b)2=(2c)2,
∴一组勾股数的2倍一定是勾股数.
例2 已知:在△ABC中,三条边长分别为a= n2-1,b=2n,c=n2+1(n>1), 求证: △ABC为直角三角形.
证明:∵a2+b2=(n2-1)2+(2n)2 =n4-2n2+1+4n2 =n4+2n2+1 =(n2+1)2=c2,
∴ △ABC是直角三角形,(勾股定理的逆定理).
4.已知:如图,△ABC中,AB=2 ,AC=2,高AD= . 求证:∠BAC=90°.
证明:∵AD是△ABC的高,
∴在Rt△ADC中,CD2+AD2=AC2,
在Rt△ADB中,BD2+AD2=AB2,
∴BC=CD+BD=4,
∴ ∠BAC=90°.
又∵AC2+AB2=4+12=16,
∴AC2+AB2=BC2,
∴△ABC是直角三角形,
(2)勾股定理的逆定理的应用.
(1)勾股定理的逆定理;
1.本节课你学习了哪些主要内容,与同伴交流.
2.通过本节课的学习你有哪些收获和经验? 谈谈你的感悟.
初中18.2 勾股定理的逆定理集体备课课件ppt: 这是一份初中18.2 勾股定理的逆定理集体备课课件ppt,共13页。PPT课件主要包含了做一做,∠C是直角吗,作业做课后练习等内容,欢迎下载使用。
沪科版八年级下册18.2 勾股定理的逆定理教案配套课件ppt: 这是一份沪科版八年级下册18.2 勾股定理的逆定理教案配套课件ppt,共13页。PPT课件主要包含了想一想,∠C是90°,动手画一画,古埃及人的探究,勾股定理的逆命题,勾股定理,逆命题,例题讲解,∴a2+b2=c2,∴b2+c2≠a2等内容,欢迎下载使用。
沪科版八年级下册18.2 勾股定理的逆定理背景图课件ppt: 这是一份沪科版八年级下册18.2 勾股定理的逆定理背景图课件ppt,共17页。PPT课件主要包含了问题情境,实践探究,互逆命题,小游戏,综合运用,小结梳理等内容,欢迎下载使用。













