

湖北省武汉市硚口区2019-2020学年七年级下期期中数学试卷(word版 含答案)
展开2019-2020学年湖北省武汉市硚口区七年级(下)期中数学试卷
一、选择题(共10小题,每题3分,共30分)下列各题均有四个备选答案,其中有且只有一个是正确的,请在答题卡上将正确答案的代号字母涂黑.
1.(3分)下列各数中是无理数的是( )
A. B. C. D.
2.(3分)的平方根是( )
A. B.﹣ C.± D.±
3.(3分)在下列所给出坐标的点中,在第二象限的是( )
A.(2,3) B.(﹣2,3) C.(﹣2,﹣3) D.(2,﹣3)
4.(3分)下列各式中,正确的是( )
A. B. C. D.
5.(3分)点M(2,﹣3)到x轴的距离是( )
A.2 B.﹣3 C.3 D.以上都不对
6.(3分)如图,点E在BC的延长线上,由下列条件不能得到AB∥CD的是( )
A.∠1=∠2 B.∠B=∠DCE
C.∠3=∠4 D.∠D+∠DAB=180°
7.(3分)如图,学校相对于小明家的位置下列描述最准确的是( )
A.距离学校1200米处
B.北偏东65°方向上的1200米处
C.南偏西65°方向上的1200米处
D.南偏西25°方向上的1200米处
8.(3分)下列命题中,是真命题的是( )
A.三条直线a、b、c在同一平面内,若a⊥b,b⊥c,则a⊥c
B.无限小数都是无理数
C.经过直线外一点,有且只有一条直线与这条直线平行
D.同旁内角互补
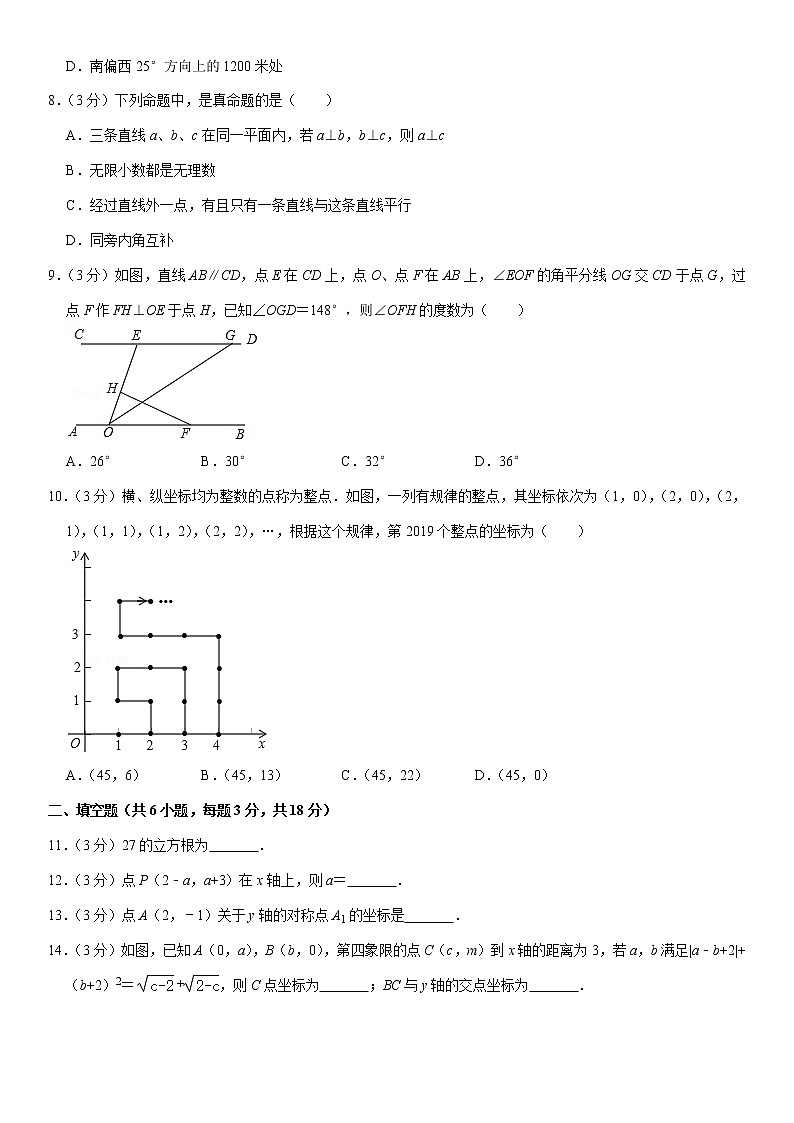
9.(3分)如图,直线AB∥CD,点E在CD上,点O、点F在AB上,∠EOF的角平分线OG交CD于点G,过点F作FH⊥OE于点H,已知∠OGD=148°,则∠OFH的度数为( )
A.26° B.30° C.32° D.36°
10.(3分)横、纵坐标均为整数的点称为整点.如图,一列有规律的整点,其坐标依次为(1,0),(2,0),(2,1),(1,1),(1,2),(2,2),…,根据这个规律,第2019个整点的坐标为( )
A.(45,6) B.(45,13) C.(45,22) D.(45,0)
二、填空题(共6小题,每题3分,共18分)
11.(3分)27的立方根为 .
12.(3分)点P(2﹣a,a+3)在x轴上,则a= .
13.(3分)点A(2,﹣1)关于y轴的对称点A1的坐标是 .
14.(3分)如图,已知A(0,a),B(b,0),第四象限的点C(c,m)到x轴的距离为3,若a,b满足|a﹣b+2|+(b+2)2=,则C点坐标为 ;BC与y轴的交点坐标为 .
15.(3分)在同一平面内,若有4条直线,则最多有 个交点;若200条直线中恰好有且只有2m条直线互相平行,则这200条直线最多有 个交点(用含有m的式子表示).
16.(3分)如图,在平面直角坐标系中,点B(0,m),点C(n,m),其中m>0,n<0,点A是x轴负半轴上一点,点P是在直线CB与直线AO之间的一点,连接BP、OP,BN平分∠CBP,ON平分∠AOP,BN交ON于N,则∠BPO与∠BNO之间可满足的数量关系式为 .
三、解答题(共8小题,共72分)
17.(1)计算:
①×﹣;
②﹣+|﹣3|+.
(2)求下列式子中的x的值:
①4(x﹣2)2=49;
②(x﹣1)3=64.
18.如图,直线AB,CD相交于点O,EO⊥AB,垂足为O.
(1)若∠EOC=35°,求∠AOD的度数;
(2)若∠BOC=2∠AOC,求∠DOE的度数.
19.完成下列证明:如图,已知AD⊥BC,EF⊥BC,∠1=∠2.
求证:∠BAC+∠AGD=180°.
证明:∵AD⊥BC,EF⊥BC(已知),
∴∠EFB=90°,∠ADB=90°( ),
∴∠EFB=∠ADB(等量代换),
∴EF∥AD( ),
∴∠1=∠BAD( ),
又∵∠1=∠2(已知),
∴∠ =∠ (等量代换),
∴DG∥BA( ),
∴∠BAC+∠AGD=180°( ).
20.如图,已知∠1=∠BDC,∠2+∠3=180°.
(1)请你判断DA与CE的位置关系,并说明理由;
(2)若DA平分∠BDC,CE⊥AE于E,∠1=70°,试求∠FAB的度数.
21.如图,已知图中A点和B点的坐标分别为(2,﹣4)和(﹣2,2).
(1)请在图中画出坐标轴建立适当的直角坐标系;
(2)写出点C的坐标为 ;
(3)连接AB、BC和CA得△ABC,在y轴有点D满足S△ABC=S△DBC,则点D的坐标为 ,S△DBC= 个平方单位;
(4)已知第一象限内有两点P(3,n+2),Q(6,n)平移线段PQ使点P、Q分别落在两条坐标轴上,则点P平移后的对应点的坐标是 .
22.某小区有一块面积为196m2的正方形空地,开发商计划在此空地上建一个面积为100m2的长方形花坛,使长方形的长是宽的2倍.请你通过计算说明开发商能否实现这个愿望?(参考数据:≈1.414,≈7.070)
23.如图1,PQ∥MN,点A,B分别在MN,QP上,∠BAM=2∠BAN,射线AM绕A点顺时针旋转至AN便立即逆时针回转,射线BP绕B点顺时针旋转至BQ便立即逆时针回转.射线AM转动的速度是每秒2度,射线BQ转动的速度是每秒1度.
(1)直接写出∠QBA的大小为 ;
(2)射线AM、BP转动后对应的射线分别为AE、BF,射线BF交直线MN于点F,若射线BP比射线AM先转动30秒,设射线AM转动的时间为t(0<t<180)秒,求t为多少时,直线BF∥直线AE?
(3)如图2,若射线BP、AM同时转动m(0<m<90)秒,转动的两条射线交于点C,作∠ACD=120°,点D在BP上,请探究∠BAC与∠BCD的数量关系.
24.如图1,在平面直角坐标系中,点A(﹣2,0),B(﹣5,0),点C在第三象限,已知AC⊥AB,且AB=AC.
(1)求点C的坐标;
(2)如图2,N为线段AC上一动点(端点除外),P是y轴负半轴的一点,连接BP、CP,射线BN与∠ACP的角平分线交于D,若∠BDC﹣∠ABD=45°,求点P的坐标;
(3)在第(2)问的基础上,如图3,点Q与点P关于x轴对称,E是射线PC上一个动点,连接QE,EF平分∠QEC,QM平分∠EQP,射线QH∥EF.试问∠MQH的度数是否发生改变?若不变,请求其度数;若改变,请指出其变化范围.
2019-2020学年湖北省武汉市硚口区七年级(下)期中数学试卷
参考答案与试题解析
一、选择题(共10小题,每题3分,共30分)下列各题均有四个备选答案,其中有且只有一个是正确的,请在答题卡上将正确答案的代号字母涂黑.
1.【答案】D
【解答】解:A.,是分数,属于有理数;
B.,是整数,属于有理数;
C.是分数,属于有理数;
D.是无理数.
故选:D.
2.【答案】C
【解答】解:∵(±)2=,
∴的平方根是±.
故选:C.
3.【答案】B
【解答】解:根据每个象限内点的坐标符号可得在第二象限内的点是(﹣2,3),
故选:B.
4.【答案】A
【解答】解:A、==4,故本选项正确;
B、=4,故本选项错误;
C、=4,故本选项错误;
D、±=±2,故本选项错误;
故选:A.
5.【答案】C
【解答】解:点M(2,﹣3)到x轴的距离是3.
故选:C.
6.【答案】C
【解答】解:A、正确,符合内错角相等,两条直线平行的判定定理;
B、正确,符合同位角相等,两条直线平行的判定定理;
C、错误,若∠3=∠4,则AD∥BE;
D、正确,符合同旁内角互补,两条直线平行的判定定理;
故选:C.
7.【答案】B
【解答】解:180°﹣115°=65°,
由图形知,学校在小明家的北偏东65°方向上的1200米处,
故选:B.
8.【答案】C
【解答】解:A、三条直线a、b、c在同一平面内,若a⊥b,b⊥c,则a∥c,本选项说法是假命题;
B、无限不循环小数都是无理数,本选项说法是假命题;
C、经过直线外一点,有且只有一条直线与这条直线平行,本选项说法是真命题;
D、两直线平行,同旁内角互补,本选项说法是假命题;
故选:C.
9.【答案】A
【解答】解:∵∠OGD=148°,
∴∠CGO=180°﹣∠OGD=32°,
∵AB∥CD,
∴∠BOG=∠CGO=32°,
∵OG平分∠EOF,
∴∠HOF=2∠BOG=64°,
∵FH⊥OE,
∴∠OHF=90°,
∴∠OFH=180°﹣∠OHF﹣∠HOF=26°,
故选:A.
10.【答案】A
【解答】解:根据图形,以最外边的矩形边长上的点为准,点的总个数等于x轴上右下角的点的横坐标的平方,
例如:发现12=1(第1个点)、32=9(第9个点)、52=25(第25个点)的坐标都在x轴上分别为(1,0)、(3,0)、(5,0).
发现22=4(第4个点)、42=16(第16个点)、62=36(第36个点)的横坐标都为1,坐标分别为(1,4)、(1,16)、(1,36);
后边不变:右下角的点的横坐标为n时,共有n平方个,
∵45平方=2025,45是奇数,
∴第2025个点是(45,0),退6个点得第2019个点是(45,6).
故选:A.
二、填空题(共6小题,每题3分,共18分)
11.【答案】见试题解答内容
【解答】解:∵33=27,
∴27的立方根是3,
故答案为:3.
12.【答案】见试题解答内容
【解答】解:∵点P(2﹣a,a+3)在x轴上,
∴a+3=0,
解得:a=﹣3.
故答案为:﹣3.
13.【答案】见试题解答内容
【解答】解:∵2的相反数是﹣2,
∴点A(2,﹣1)关于y轴的对称点A1的坐标是 (﹣2,﹣1),
故答案为(﹣2,﹣1).
14.【答案】见试题解答内容
【解答】解:∵,都有意义,
∴c=2,
∴|a﹣b+2|+(b+2)2=0,
∴,
解得:,
∵第四象限的点C(c,m)到x轴的距离为3,
∴C点坐标为:(2,﹣3),
设直线BC解析式为:y=kx+d,
把(﹣2,0),(2,﹣3)代入得:
,
解得:,
故BC解析式为:y=﹣x﹣,
当x=0时,y=﹣,
故直线BC与y轴的交点坐标为:(0,﹣).
故答案为:(2,﹣3),(0,﹣).
15.【答案】见试题解答内容
【解答】解:如图:2条直线相交有1个交点;
3条直线相交有1+2个交点;
4条直线相交有1+2+3个交点;
5条直线相交有1+2+3+4个交点;
6条直线相交有1+2+3+4+5个交点;
…
n条直线相交有1+2+3+…+n=n(n﹣1)个交点;
则200条直线相交有×200×(200﹣1)=19900个交点,
∵200条直线中恰好有且只有2m条直线互相平行,
∴少2m2﹣m个交点,
则这200条直线最多有(﹣2m2+m+19900)个交点.
故答案为:6;(﹣2m2+m+19900).
16.【答案】∠BNO+∠BPO=180°或∠BPO=2∠BNO.
【解答】解:①如图1,当点P在OB左侧时,∠BPO=2∠BNO.
理由如下:在△BPO中,∠PBO+∠POB=180°﹣∠BPO,
∵BC∥OA,BN平分∠CBP,ON平分∠AOP,
∴∠NBP+∠NOP=(180°﹣∠PBO﹣∠POB),
在△NOB中,∠BNO=180°﹣(∠NBP+∠NOP+∠PBO+∠POB),
=180°﹣[(180°﹣∠PBO﹣∠POB)+∠PBO+∠POB],
=90°﹣(∠PBO+∠POB),
=90°﹣(180°﹣∠BPO),
=∠BPO,
∴∠BPO=2∠BNO;
②如图2,当点P在OB右侧时,∠BNO+∠BPO=180°.
理由如下:∵BC∥OA,
∴∠CBP+∠AOP+∠BPO=360°,
∵BN平分∠CBP,ON平分∠AOP,
∴∠PBN+∠PON+∠BPO=×360°=180°,
∴∠PBN+∠PON=180°﹣∠BPO,
在四边形BNOP中,∠BNO=360°﹣∠PBN﹣∠PON﹣∠BPO=360°﹣(180°﹣∠BPO)﹣∠BPO=180°﹣∠BPO,
∴∠BNO+∠BPO=180°.
故答案为:∠BNO+∠BPO=180°或∠BPO=2∠BNO.
三、解答题(共8小题,共72分)
17.【答案】见试题解答内容
【解答】解:(1)①原式=﹣×﹣2
=﹣2;
②原式=﹣5+3﹣+
=﹣;
(2)①∵4(x﹣2)2=49,
∴,
∴,
∴,
∴或.
②∵(x﹣1)3=64,
∴x﹣1=4,
∴x=5.
18.【答案】见试题解答内容
【解答】解:(1)∵EO⊥AB,
∴∠BOE=90°,
∵∠EOC=35°,
∴∠BOC=∠BOE+∠EOC=125°﹒
∴∠AOD=∠BOC=125°,
答:∠AOD的度数为125°;
(2)∵∠AOC+∠BOC=180°,∠BOC=2∠AOC,
∴∠AOC+2∠AOC=180°
∴∠AOC=60°,
∴∠BOD=∠AOC=60°,
∴∠EOD=∠BOE+∠BOD=90°+60°=150°,
答:∠DOE的度数为150°.
19.【答案】见试题解答内容
【解答】解:∵AD⊥BC,EF⊥BC(已知),
∴∠EFB=90°,∠ADB=90°(垂直定义),
∴∠EFB=∠ADB(等量代换),
∴EF∥AD(同位角相等,两直线平行),
∴∠1=∠BAD(两直线平行,同位角相等),
又∵∠1=∠2(已知),
∴∠2=∠BAD(等量代换),
∴DG∥BA(内错角相等,两直线平行),
∴∠BAC+∠AGD=180°(两直线平行,同旁内角互补).
故答案为:垂直定义;同位角相等,两直线平行;两直线平行,同位角相等;2;BAD;内错角相等,两直线平行;两直线平行,同旁内角互补.
20.【答案】见试题解答内容
【解答】解:(1)AD∥EC,
理由是:∵∠1=∠BDC,
∴AB∥CD,
∴∠2=∠ADC,
又∵∠2+∠3=180°,
∴∠ADC+∠3=180°,
∴AD∥EC.
(2)∵DA平分∠BDC,
∴∠ADC=∠BDC=35°,
∴∠2=∠ADC=35°,
∵CE⊥AE,AD∥EC,
∴∠FAD=∠AEC=90°,
∴∠FAB=∠FAD﹣∠2=90°﹣35°=55°.
21.【答案】见试题解答内容
【解答】解:(1)建立如图所示的平面直角坐标系;
(2)点C的坐标为(3,2);
(3)设D到BC的距离为h,
∵S△ABC=S△DBC,
∴=•h×5,
解得:h=6,
∴点D的坐标为(0,﹣4)或(0,8),
∴S△DBC=×5×6=15个(平方单位);
(4)解:设平移后点P、Q的对应点分别是P′、Q′.
分两种情况:
①P′在y轴上,Q′在x轴上,
则P′横坐标为0,Q′纵坐标为0,
∴n=0,
∴点P平移后的对应点的坐标是(0,2);
②P′在x轴上,Q′在y轴上,
则P′纵坐标为0,Q′横坐标为0,
∴3﹣6=﹣3,
∴点P平移后的对应点的坐标是(﹣3,0);
综上可知,点P平移后的对应点的坐标是(0,2)或(﹣3,0).
故答案为:(2)(3,2);(3)(0,﹣4)或(0,8),15;(4)(0,2)或(﹣3,0).
22.【答案】见试题解答内容
【解答】解:长方形花坛的宽为xm,长为2xm.
2x•x=100,
∴x2=50,
∵x>0,
∴x=,2x=2,
∵正方形的面积=196m2,
∴正方形的边长为14m,
∵2>14,
∴当长方形的边与正方形的边平行时,开发商不能实现这个愿望.
长方形花坛如图放置,设宽为2xm,长为4xm.
∵正方形ABCD的面积为196m2,
∴AB=14(m),AC=14(m),
由题意2x+4x=14,
∴x=,
∴长方形EFGH的面积=8x2≈87.1<100,
∴开发商不能实现这个愿望.
综上所述,开发商不能实现这个愿望.
23.【答案】(1)60°;
(2)t=30秒或110秒;
(3)∠BAC=2∠BCD,
【解答】解:(1)∵PQ∥MN,
∴∠QBA=∠BAN,
∵∠BAM+∠BAN=180°,∠BAM=2∠BAN,
∴3∠BAN=180°,
∴∠BAN=60°,
∴∠QBA=∠BAN=60°,
故答案为:60°;
(2)①当0<t<90时,如图1,
∵PQ∥MN,
∴∠PBF=∠BFA,
∵AE∥BF,
∴∠EAM=∠BFA,
∴∠EAM=∠PBF,
∴2t=1•(30+t),
解得t=30;
②当90<t<150时,如图2,
∵PQ∥MN,
∴∠PBF+∠BFA=180°,
∵AE∥BF,
∴∠EAN=∠BFA,
∴∠PBF+∠EAN=180°,
∴1•(30+t)+(2t﹣180)=180,
解得t=110,
综上所述,当t=30秒或110秒时BF∥直线AE;
(3)∠BAC=2∠BCD,理由如下:
如图3,作CH∥PQ,
∵PQ∥MN,
∴CH∥PQ∥MN,
∴∠QBC+∠2=180°,∠MAC+∠1=180°,
∴∠QBC+∠2+∠MAC+∠1=360°,
∵∠QBC=180°﹣m°,∠MAC=2m°,
∴∠BCA=∠1+∠2=360°﹣(180°﹣m°)﹣2m°=180°﹣m°,
而∠ACD=120°,
∴∠BCD=120°﹣∠BCA=120°﹣(180°﹣m°)=m°﹣60°,
∵∠CAN=180°﹣2m°,
∴∠BAC=60°﹣(180°﹣2m°)=2m°﹣120°,
∴∠BAC:∠BCD=2:1,
即∠BAC=2∠BCD.
24.【答案】见试题解答内容
【解答】解:(1)∵A(﹣2,0),B(﹣5,0),AB=AC,
∴AB=AC=3,
∴C(﹣2,﹣3);
(2)如图,作DH⊥AC于H点,
∵DH⊥AC,AC⊥AB,
∴∠BAC=∠OAC=∠DHA=∠DHC=90°,
∴AB∥DH,
∴∠ABD=∠BDH,
∴∠HDC=∠BDC﹣∠BDH=∠BDC﹣∠ABD=45°,
∴∠DCH=90°﹣∠HDC=45°,
∵CD平分∠ACP,
∴∠ACP=2∠DCH=90°=∠BAC,
∴CP∥AB,
∴P(0,﹣3);
(3)答:∠MQH的度数不变,且∠MQH=45°,
如图,作EG∥y轴,设QH与x轴交于N,
由第(2)问得CP∥AB,
∴∠CPQ=∠PON=90°,
∵EG∥y轴,
∴∠GEC=∠OPC=90°,∠GEQ=∠EQP,
∵∠QEC=∠GEQ+∠GEC=∠EQP+∠QPE=∠EQP+90°①,
∵EF平分∠QEC,QM平分∠EQP,
∴设∠QEF=∠FEC=β,∠EQM=∠MQP=α,
①式即为2β=2α+90°,
∴β﹣α=45°,
∵QH∥EF,
∴∠HQE=∠QEF=β,
∴∠MQH=∠HQE﹣∠MQE=β﹣α=45°.
湖北省武汉市硚口区2023-2024学年七年级上学期期中数学试卷: 这是一份湖北省武汉市硚口区2023-2024学年七年级上学期期中数学试卷,共9页。
2021-2022学年湖北省武汉市硚口区七年级(下)期末数学试卷(Word解析版): 这是一份2021-2022学年湖北省武汉市硚口区七年级(下)期末数学试卷(Word解析版),共22页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
湖北省武汉市硚口区2021-2022学年七年级(下)期中数学试卷(含解析): 这是一份湖北省武汉市硚口区2021-2022学年七年级(下)期中数学试卷(含解析),共21页。试卷主要包含了【答案】B,【答案】C,【答案】D等内容,欢迎下载使用。












