2021年春季人教版七年级下册同步练习：5.2平行线及其判定

这是一份2021年春季人教版七年级下册同步练习：5.2平行线及其判定，共1页。

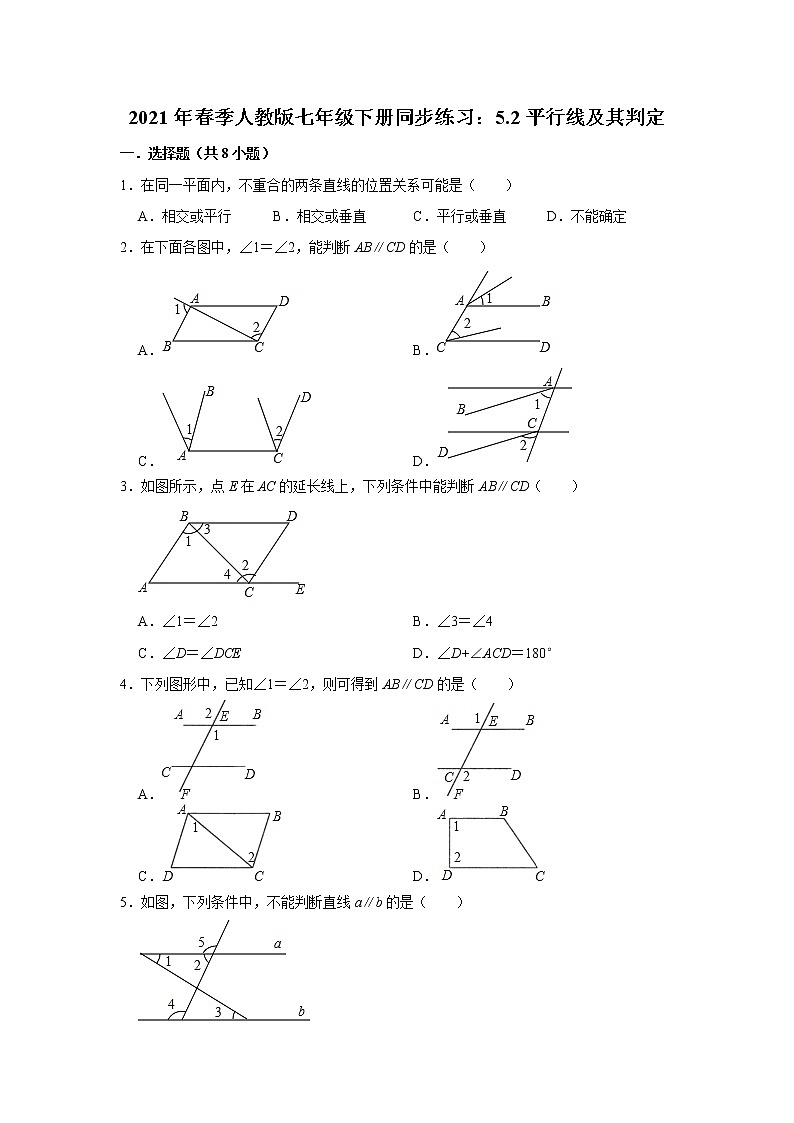
1．在同一平面内，不重合的两条直线的位置关系可能是（ ）
A．相交或平行B．相交或垂直C．平行或垂直D．不能确定
2．在下面各图中，∠1＝∠2，能判断AB∥CD的是（ ）
A．B．
C．D．
3．如图所示，点E在AC的延长线上，下列条件中能判断AB∥CD（ ）
A．∠1＝∠2B．∠3＝∠4
C．∠D＝∠DCED．∠D+∠ACD＝180°
4．下列图形中，已知∠1＝∠2，则可得到AB∥CD的是（ ）
A．B．
C．D．
5．如图，下列条件中，不能判断直线a∥b的是（ ）
A．∠1＝∠3B．∠2+∠4＝180°C．∠4＝∠5D．∠2＝∠3
6．如果a∥b，b∥c，那么a∥c，这个推理的依据是（ ）
A．等量代换
B．两直线平行，同位角相等
C．平行公理
D．平行于同一直线的两条直线平行
7．下列语句：
①不相交的两条直线叫平行线
②在同一平面内，两条直线的位置关系只有两种：相交和平行
③如果线段AB和线段CD不相交，那么直线AB和直线CD平行
④如果两条直线都和第三条直线平行，那么这两条直线平行
⑤过一点有且只有一条直线与已知直线平行
正确的个数是（ ）
A．1B．2C．3D．4
8．已知在同一平面内有三条不同的直线a，b，c，下列说法错误的是（ ）
A．如果a∥b，a⊥c，那么b⊥cB．如果b∥a，c∥a，那么b∥c
C．如果b⊥a，c⊥a，那么b⊥cD．如果b⊥a，c⊥a，那么b∥c
二．填空题（共4小题）
9．若a∥b，l∥a，则l与b的位置关系是 ．
10．在同一平面内，不重合的两条直线有 种位置关系，它们是 ．
11．小泽在课桌上摆放了一副三角板，如图所示，得到 ∥ ，依据是 ．
12．如图，已知∠B＝40°，要使AB∥CD，需要添加一个条件，这个条件可以是 ．
三．解答题（共6小题）
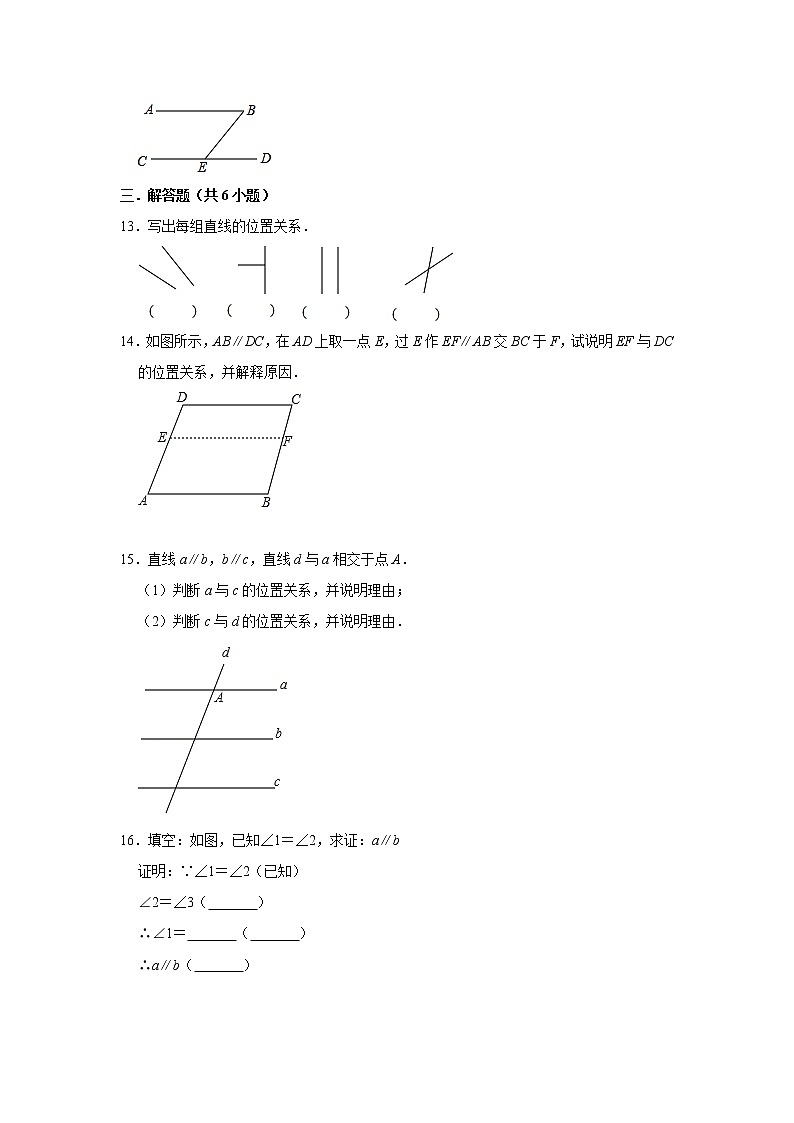
13．写出每组直线的位置关系．
14．如图所示，AB∥DC，在AD上取一点E，过E作EF∥AB交BC于F，试说明EF与DC的位置关系，并解释原因．
15．直线a∥b，b∥c，直线d与a相交于点A．
（1）判断a与c的位置关系，并说明理由；
（2）判断c与d的位置关系，并说明理由．
16．填空：如图，已知∠1＝∠2，求证：a∥b
证明：∵∠1＝∠2（已知）
∠2＝∠3（ ）
∴∠1＝ （ ）
∴a∥b（ ）
17．如图，∠EBC+∠EFA＝180°，∠A＝∠C．求证：AB∥CE．
18．如图，直线MN分别交AB和CD于点E、F，点Q在PM上，∠EPM＝∠FQM，且∠AEP＝∠CFQ，求证：AB∥CD．
参考答案
一．选择题（共8小题）
1．【解答】解：平面内的直线有平行或相交两种位置关系．
故选：A．
2．【解答】解：第一个图中，∠1、∠2不是两条直线被第三条直线所截的内错角或同位角，不能判定AB∥CD；
第二个图中，∠1、∠2不是两条直线被第三条直线所截的同位角，不能判定AB∥CD；
第三个图中，∠1、∠2不是两条直线被第三条直线所截的同位角，不能判定AB∥CD；
第四个图中，∠1、∠2是两条直线被第三条直线所截的同位角，能判定AB∥CD；
故选：D．
3．【解答】解：A、根据内错角相等，两直线平行可得AB∥CD，故此选项正确；
B、根据内错角相等，两直线平行可得BD∥AC，故此选项错误；
C、根据内错角相等，两直线平行可得BD∥AC，故此选项错误；
D、根据同旁内角互补，两直线平行可得BD∥AC，故此选项错误；
故选：A．
4．【解答】解：A、∠1和∠2的是对顶角，不能判断AB∥CD，此选项不正确；
B、∠1和∠2的对顶角是内错角，又相等，所以AB∥CD，此选项正确；
C、∠1和∠2的是内错角，又相等，故AD∥BC，不是AB∥CD，此选项错误；
D、∠1和∠2互为同旁内角，同旁内角相等两直线不平行，此选项错误．
故选：B．
5．【解答】解：A、∵∠1＝∠3，
∴a∥b，（内错角相等，两直线平行），故此选项错误；
B、∵∠2+∠4＝180°，
∴a∥b，（同旁内角互补，两直线平行），故此选项错误；
C、∵∠4＝∠5，
∴a∥b，（同位角相等，两直线平行），故此选项错误；
D、∠2＝∠3，无法判定直线a∥b，故此选项正确．
故选：D．
6．【解答】解：∵a∥b，b∥c，a、c不重合，
∴a∥c（平行于同一直线的两条直线平行）．
故选：D．
7．【解答】解：①不相交的两条直线叫平行线，必须是在同一平面内，故错误；
②在同一平面内，两条直线的位置关系只有两种：相交和平行，正确
③如果线段AB和线段CD不相交，那么直线AB和直线CD平行，错误；
④如果两条直线都和第三条直线平行，那么这两条直线平行，正确；
⑤过直线外一点有且只有一条直线与已知直线平行，故错误，
故选：B．
8．【解答】解：A、如果a∥b，a⊥c，那么b⊥c，说法正确；
B、如果b∥a，c∥a，那么b∥c，说法正确；
C、如果b⊥a，c⊥a，那么b⊥c，说法错误；
D、如果b⊥a，c⊥a，那么b∥c，说法正确；
故选：C．
二．填空题（共4小题）
9．【解答】解：∵a∥b，l∥a，
∴l∥b，
故答案为：l∥b．
10．【解答】解：在同一平面内，不重合的两条直线有2种位置关系，它们是相交或平行．
11．【解答】解：由图可得，∠ACD＝∠FDC＝90°，
∴AC∥DF（内错角相等，两直线平行）．
故答案为：AC，DF，内错角相等，两直线平行．
12．【解答】解：当∠B＝∠BED时，AB∥CD，
所以添加∠BED＝40°时，可得到AB∥CD．
故答案为∠BED＝40°．
三．解答题（共6小题）
13．【解答】解：第一组：两直线相交；
第二组：两直线垂直；
第三组：两直线平行；
第四组：两直线相交．
14．【解答】解：∵AB∥DC，EF∥AB，
∴EF∥DC（平行公理）．
15．【解答】解：（1）a与c的位置关系是平行，
理由是：∵直线a∥b，b∥c，
∴a∥c；
（2）c与d的位置关系是相交，
理由是：∵c∥a，直线d与a相交于点A，
∴c与d的位置关系是相交．
16．【解答】证明：∵∠1＝∠2（已知）
∠2＝∠3（对顶角相等）
∴∠1＝∠3（等量代换）
∴a∥b（同位角相等，两直线平行），
故答案为：对顶角相等；∠3；等量代换；同位角相等，两直线平行
17．【解答】证明：∵∠EBC+∠EFA＝180°，∠DFB＝∠EFA，
∴∠EBC+∠DFB＝180°，
∴BC∥AD，
∴∠EDA＝∠C．
∵∠A＝∠C，
∴∠EDA＝∠A，
∴AB∥CE．
18．【解答】解：如图，
∵∠EPM＝∠FQM，∠AEP＝∠CFQ，∠EPM+∠AEP+∠1＝180°，∠FQM+∠CFQ+∠2＝180°，
∴∠1＝∠2，
∴AB∥CD．