人教版九年级下册第二十八章 锐角三角函数28.2 解直角三角形及其应用教学演示ppt课件

这是一份人教版九年级下册第二十八章 锐角三角函数28.2 解直角三角形及其应用教学演示ppt课件，共14页。PPT课件主要包含了3边角之间的关系，解依题意可知，学习目标，水平线，BCDC40m，在Rt△ACD中，解直角三角形等内容，欢迎下载使用。

1、直角三角形中除直角外五个元素之间具有什么关系？ 2、在Rt△ABC 中，已知a =12,c =13，求∠B 应该用哪个关系？请计算出来.
(1) 三边之间的关系
（2）两锐角之间的关系
创设情景 明确目标
1．使学生了解仰角、俯角的概念，使学生根据直角三角形的知识解决实际问题．2．逐步培养学生分析问题、解决问题的能力．
活动1： 2012年6月18日，“神舟”九号载人航天飞船与“天宫”一号目标飞行器成功实现交会对接.“神舟”九号与“天宫”一号的组合体在离地球表面343km的圆形轨道上运行，如图，当组合体运行到地球表面P点的正上方时，从中能直接看到的地球表面最远的点在什么位置？最远点与P点的距离是多少（地球半径约为6400km，π取3.142，结果取整数）？
分析：从组合体中能直接看到的地球表面最远点，是视线与地球相切时的切点．
探究点一：构造直角三角形解题
合作探究 达成目标
解：在图中，FQ是⊙O的切线，△FOQ是直角三角形．
由此可知，当组合体在P点正上方时，从中观测地球表面时的最远点距离P点约为2051km.
小组讨论1:从活动1中的例题解答中，你能体会到解直角三角形的应用前提条件是什么吗？如何进行？
【反思小结】一般情况下，直角三角形是求解或运用三角函数值的前提条件，故当题目中提供的并非直角三角形时，需添加辅助线构造直角三角形，然后运用三角函数解决问题．
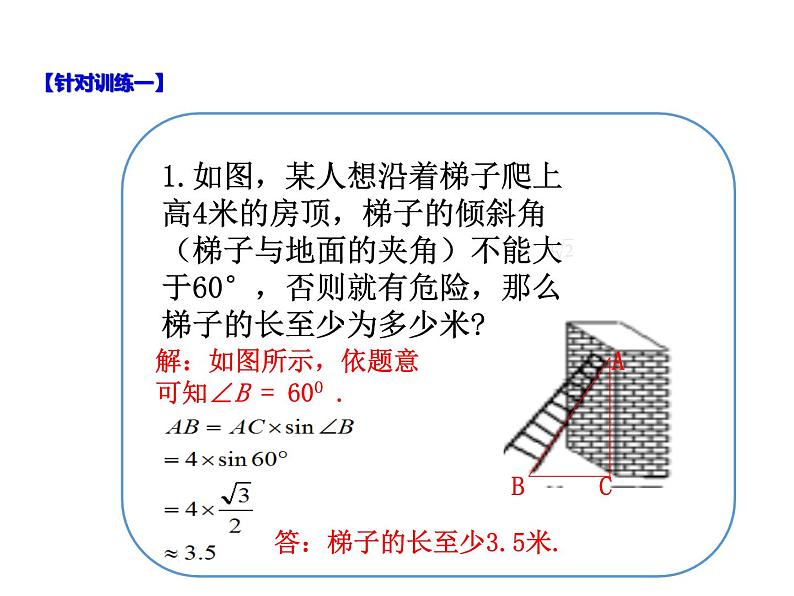
1.如图，某人想沿着梯子爬上高4米的房顶，梯子的倾斜角（梯子与地面的夹角）不能大于60°，否则就有危险，那么梯子的长至少为多少米?
解：如图所示，依题意可知∠B = 600 .
答：梯子的长至少3.5米.
活动2: 热气球的探测器显示，从热气球看一栋高楼顶部的仰角为30°，看这栋高楼底部的俯 角为60°，热气球与高楼的水平距离为120m，这栋高楼有多高（结果精确到0.1m）?
分析：我们知道，在视线与水平线所成的角中,视线在水平线上方的是仰角，视线在水平线下方的是俯角.因此，在图中，a=30°,β=60°.
Rt△ABC 中，a =30°，AD＝120，所以利用解直角三角形的知识求出BD；类似地可以求出CD，进而求出BC．
探究点二：测量物体的高度问题
解：如图，a = 30°,β= 60°， AD＝120．
答：这栋楼高约为277.1m
小组讨论2:从活动2中例题的解答中，你体会到什么思想方法？如何添加辅助线构造可解的直角三角形？
【反思小结】利用直角三角形中的边角关系求线段的长度，如果涉及两个或两个以上的三角形时，可以通过设未知数，利用线段之间的等量关系列出方程，从而求解 ．
1. 建筑物BC上有一旗杆AB，由距BC40m的D处观察旗杆顶部A的仰角54°，观察底部B的仰角为45°，求旗杆的高度（精确到0.1m）.
解：在等腰三角形BCD中∠ACD=90°,
所以AB=AC－BC=55.2－40=15.2.
答：旗杆的高度为15.2m.
1．在解决例3的问题时，我们综合运用了_____和_____________的知识.2．当我们进行测量时，在视线与______线所成的角中，视线在______线上方的角叫做仰角，在______线下方的角叫做俯角．
1．如图（2），在高出海平面100米的悬崖顶A处，观测海平面上一艘小船B，并测得它的俯角为45°，则船与观测者之间的水平距离BC=__ _______米.2．如图（3），两建筑物AB和CD的水平距离为30米，从A点测得D点的俯角为30°，测得C点的俯角为60°，则建筑物CD的高为_____米.