初中数学18.1.1 平行四边形的性质图文ppt课件

这是一份初中数学18.1.1 平行四边形的性质图文ppt课件，共29页。PPT课件主要包含了学习目标，生活中的数学，平行四边，研学教材，探究新知，知识普及，∠1＝∠2，ACAC，∠3∠4，△CDA等内容，欢迎下载使用。

1、掌握平行四边形的概念和平行四边形对边相等、对角相等的性质；
2、会用平行四边形的性质解决简单的平行四边形的计算问题.
1、如图，你能观察到图中有我们学过的_____________形.
2、举出生活中常见的平行四边形的一些其它例子，有_____________________________________________________________.
小区的伸缩门，庭院的竹篱笆，载重汽车的防护栏，教室的门框、黑板等
认真阅读课本p41至p43页的内容，体验知识点的形成过程.
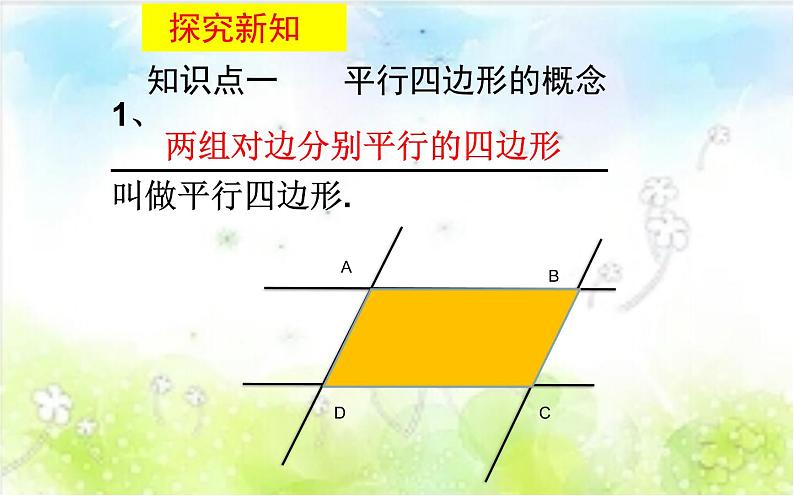
知识点一 平行四边形的概念
两组对边分别平行的四边形
1、___________________________ 叫做平行四边形.
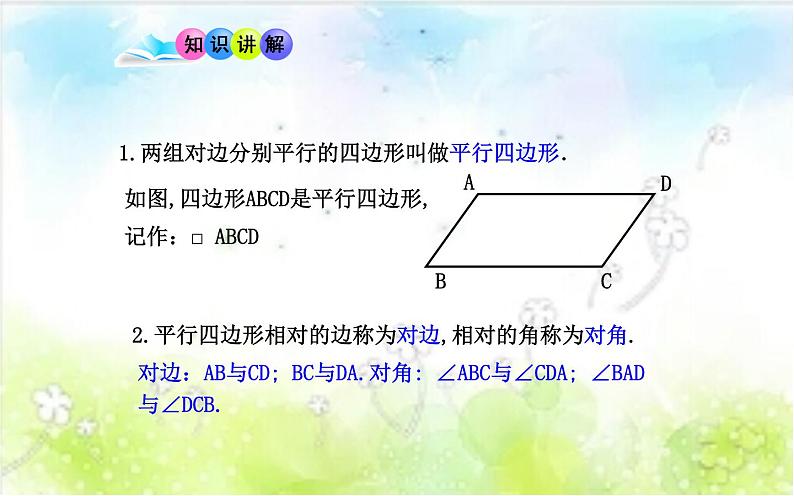
1.两组对边分别平行的四边形叫做平行四边形．
如图,四边形ABCD是平行四边形,记作：□ ABCD
2.平行四边形相对的边称为对边,相对的角称为对角.
对边：AB与CD; BC与DA.对角: ∠ABC与∠CDA; ∠BAD与∠DCB.
平行四边形的对边、对角有怎样的数量关系？
　　请用直尺、量角器等工具度量（课本41页）平行四边形的边和角，并记录下数据，验证猜想AB=DC，AD=BC，∠A=∠C，∠B=∠D是否正确?
用你以前所学的知识证明猜想.
AB=DC=2cm，AD=BC=2.5cm，∠A=∠C=120 ° ，∠B=∠D=60 °
用两个全等的三角形纸片可以拼出几种形状不同的平行四边形？
从拼图中可以得到什么启示？
平行四边形可以由两个全等的三角形组成，因此在解决平行四边形的问题时，通常可以连接对角线转化为两个全等的三角形进行解题.
已知：如图，四边形ABCD为平行四边形.求证：AB =CD，AD=BC，∠A=∠C，∠B=∠D.
证明：如图，连接 . ∵四边形ABCD为平行四边形， ∴ ∥ , ∥ , ∴ =___ ， =_____ . 在△ABC和△CDA中 _____________ _____________(公共边) _____________∴△ABC ≌_______（_____ ）.
∴ =____ ， =_____， =_____ .∴∠1_____∠2，∠3_____∠4∵∠1+∠4_____∠2+∠3∴
知识点二 平行四边形的性质
平行四边形的性质：平行四边形的对边______ ；平行四边形的对角_______ .
已知：如图，四边形ABCD为平行四边形.求证：∠A=∠C， ∠B=∠D.
不添加辅助线直接运用平行四边形的定义证明其对角相等.
证明：∵四边形ABCD为平行四边形,∴
AB∥CD，AD∥BC .
∴∠A+∠D=180°,∠B+∠C=180°； ∠A+∠B=180°，∠C+∠D=180°.（两直线平行，同旁内角互补.）∴
∠A=∠C，∠B=∠D.
平行四边形的对边相等．平行四边形的对角相等．
平行四边形的性质除了对边互相平行以外，还有:
∵ 四边形ABCD是平行四边形
∴ AB＝CD， AD＝BC．（平行四边形的对边相等）
∠A= ∠C, ∠B= ∠D.（平行四边形的对角相等）
如图，在 ABCD中.(1)若∠A =32。,求其余三个角的度数.
∵四边形ABCD是平行四边形
且 ∠A =32。(已知),
∴ ∠A = ∠C=32。, ∠B= ∠D (平行四边形的对角相等).
又∵AD∥BC（平行四边形的对边平行）,
∴ ∠A + ∠B =180。(两直线平行，同旁内角互补),
∴ ∠B= ∠D= 180。- ∠A = 180。- 32。=148。.
(2)连接AC，已知 ABCD的周长等于20 cm，AC=7cm，求△ABC的周长.
解：∵四边形ABCD是平行四边形(已知), ∴AB=CD，BC=AD(平行四边形的对边相等). 又∵AB+BC+CD+AD=20cm(已知), ∴AB+BC= 10cm. ∵AC=7cm, ∴ △ABC的周长为AB+BC+AC= 17cm.
1.在 ABCD中，（1）已知AB=5，BC=3，求它的周长；（2）已知∠A=38°，求其余各内角的度数
（1）解： ABCD的周长＝2（AB+BC） ＝2（5+3） ＝16.
（2）解：∵四边形ABCD为平行四边形, ∴∠C=∠A=38° （平行四边形的对角相等）， ∵AD∥BC（平行四边形的概念）， ∴∠A+∠B=180°， ∴∠B=180°－∠A=180°－38°=142° ∴∠D=∠B=142° （平行四边形的对角相等）
结论 已知平行四边形一个内角的度数，那么其它内角的度数也_______确定（填“能”或“不能”）.
证明： ∵四边形ABCD是平行四边形，∴ ∠A= ∠C，AD=CB.又∠AED= ∠CFB=90°，∴ △ADE≌△CBF（AAS）,∴AE=CF.
思考 在上述证明中还能得出什么结论？
若m // n，作 AB // CD // EF，分别交 m于A、C、E，交 n于B、D、F.
由平行四边形的性质得AB=CD=EF.
两条平行线之间的平行线段相等.
由平行四边形的定义易知四边形ABCD，CDEF均为平行四边形.
两条平行线间的距离相等.
若m // n，AB、CD、EF垂直于 n，交n于B、D、F，交 m于A、C、E.
同前面易得AB=CD=EF
两条平行线间的距离：两条平行线中，一条直线上任意一点到另一条直线的距离
课本P43:2.剪两张对边平行的纸条随意交叉叠放在一起，重合部分构成了一个四边形，转动其中一张纸条，线段AD和BC的长度有什么关系？为什么？
解：AD和BC的长度相等.理由如下：由题意知AB//CD,AD//BC，∴四边形ABCD是平行四边形，∴AD=BC.
1.在□ABCD中，M是BC延长线上的一点，若∠A=135°，则∠MCD的度数是（ ） A .45° B. 55° C. 65° D. 75°
2.有一块形状如图 所示的玻璃，不小心把EDF部分打碎了，现在只测得AE=60cm，BC=80cm，∠B=60°且AE∥BC、AB∥CF,你能根据测得的数据计算出DE的长度和∠D的度数吗？
解：∵AE//BC，AB//CF，
∴四边形ABCD是平行四边形.
∴∠D=∠B=60°，AD=BC=80cm.
∴ED=AD-AE=20cm.
答：DE的长度是20cm, ∠D的度数是60°.
2、平行四边形的性质：___________________________________________________________.
1、_______________________________ 叫做平行四边形.
平行四边形的对边相等 ；平行四边形的对角相等
3、两条平行线之间的任何两条___________都相等. 两条平行线中，____________________________________________________，叫做这两条平行线之间的距离.
一条直线上任意一点到另一条直线的距离