初中数学人教版九年级上册22.3 实际问题与二次函数优秀ppt课件

这是一份初中数学人教版九年级上册22.3 实际问题与二次函数优秀ppt课件，共21页。PPT课件主要包含了知识回顾，最大利润问题，建立函数关系式，确定自变量取值范围，确定最大利润，学习目标，课堂导入，知识点1，新知探究，跟踪训练等内容，欢迎下载使用。

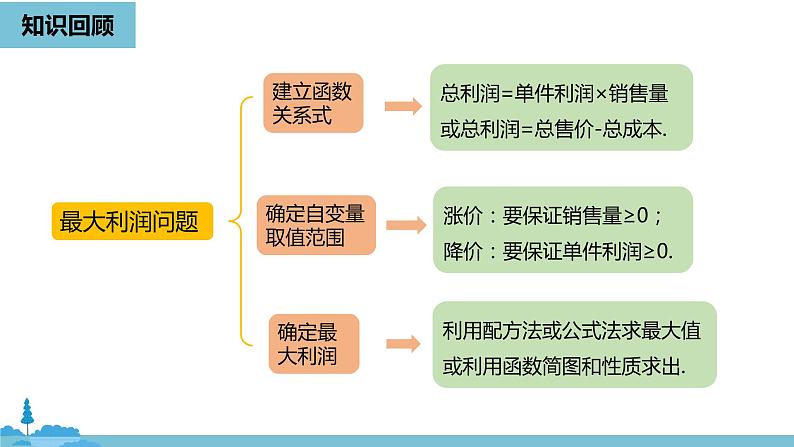
总利润=单件利润×销售量或总利润=总售价-总成本.
涨价：要保证销售量≥0；降价：要保证单件利润≥0.
利用配方法或公式法求最大值或利用函数简图和性质求出.
1.掌握二次函数模型的建立，会把实际问题转化为二次函数问题．
2.利用二次函数解决拱桥及运动中的有关问题．
3.能运用二次函数的图象与性质进行决策．
前面我们已经学习了利用二次函数解决几何最值问题及实际问题中的最值问题，本节课我们继续学习利用二次函数解决拱桥、隧道、以及一些运动类的“抛物线”型问题.
图中是抛物线形拱桥，当拱顶离水面 2 m时，水面宽 4 m．水面下降 1 m，水面宽度增加多少？
设这条抛物线表示的二次函数为y＝ax2.由抛物线经过点(2，－2)，可得－2＝a×22，a＝－这条抛物线表示的二次函数为y＝－ x2.当水面下降1 m时，水面的纵坐标为－3.当 y = -3时，- x2= -3，解得 x1= ，x2= - ，所以当水面下降1 m时，水面宽度为 m.水面下降1 m，水面宽度增加________m.
解决抛物线型建筑问题的步骤：(1)建立适当的平面直角坐标系，将抛物线形的图形放在坐标系中；(2)设出函数解析式，结合图形和已知条件，用待定系数法求函数解析式；(3)利用二次函数的图象与性质求解实际问题.
一条单车道的抛物线形隧道如图所示.隧道中公路的宽度 AB=8 m，隧道的最高点 C 到公路的距离为 6 m.(1)建立适当的平面直角坐标系，求抛物线的解析式；
一条单车道的抛物线形隧道如图所示.隧道中公路的宽度 AB=8 m，隧道的最高点 C 到公路的距离为 6 m.(2)现有一辆货车的高度是 4.4 m，货车的宽度是 2 m.为了保证安全，车顶距离隧道顶部至少 0.5 m，通过计算说明这辆货车能否安全通过这条隧道.
解决抛物线型运动路线问题时：一定要分析清楚抛物线的横、纵坐标的实际意义，再利用二次函数的图象和性质解题.
如图，某河面上有一座抛物线形拱桥，桥下水面在正常水位 AB时，宽为 20 m，若水位上升 3 m，水面就会达到警戒线 CD，这时水面宽度为 10 m.(1) 建立适当的平面直角坐标系并求出抛物线的解析式；
如图，某河面上有一座抛物线形拱桥，桥下水面在正常水位 AB时，宽为 20 m，若水位上升 3 m，水面就会达到警戒线 CD，这时水面宽度为 10 m.(2) 若洪水到来时，水位以每小时 0.2 m 的速度上升，从警戒线开始，再持续多少小时就能到达拱桥的拱顶？
解：当y取得最大值时，飞机停下来，则y=60t-1.5t2=-1.5(t-20)2+600，当t=20时，y取得最大值，即飞机着陆后滑行20 s时，滑行距离为600米．因此 t 的取值范围是0≤t≤20；当t=16时，y=576，所以最后 4 s滑行的距离是600-576=24(米)．
（二次函数的图象和性质）
（实物中的抛物线形问题）
能够将实际距离准确的转化为点的坐标；选择运算简便的方法.
发射一枚炮弹，经过 x 秒后炮弹的高度为 y 米，x，y 满足 y=ax2+bx，其中 a，b 是常数，且 a≠0.若此炮弹在第 6 秒与第 14 秒时的高度相等，则炮弹达到最大高度的时刻是( )
A.第8秒B.第10秒C.第12秒D.第15秒
一位篮球运动员在距离篮圈中心水平距离 4 m 处起跳投篮，球沿一条抛物线运动，当球运动的水平距离为 2.5 m 时，达到最大高度 3.5 m，然后准确落入篮框内，已知篮圈中心距离地面高度为 3.05 m，在如图所示的平面直角坐标系中，下列说法正确的是 ( )