初中人教版第二十九章 投影与视图综合与测试优秀综合训练题

第二十九章 投影与视图 综合检测试卷

(满分：120分)

一、选择题(每小题3分，共30分)

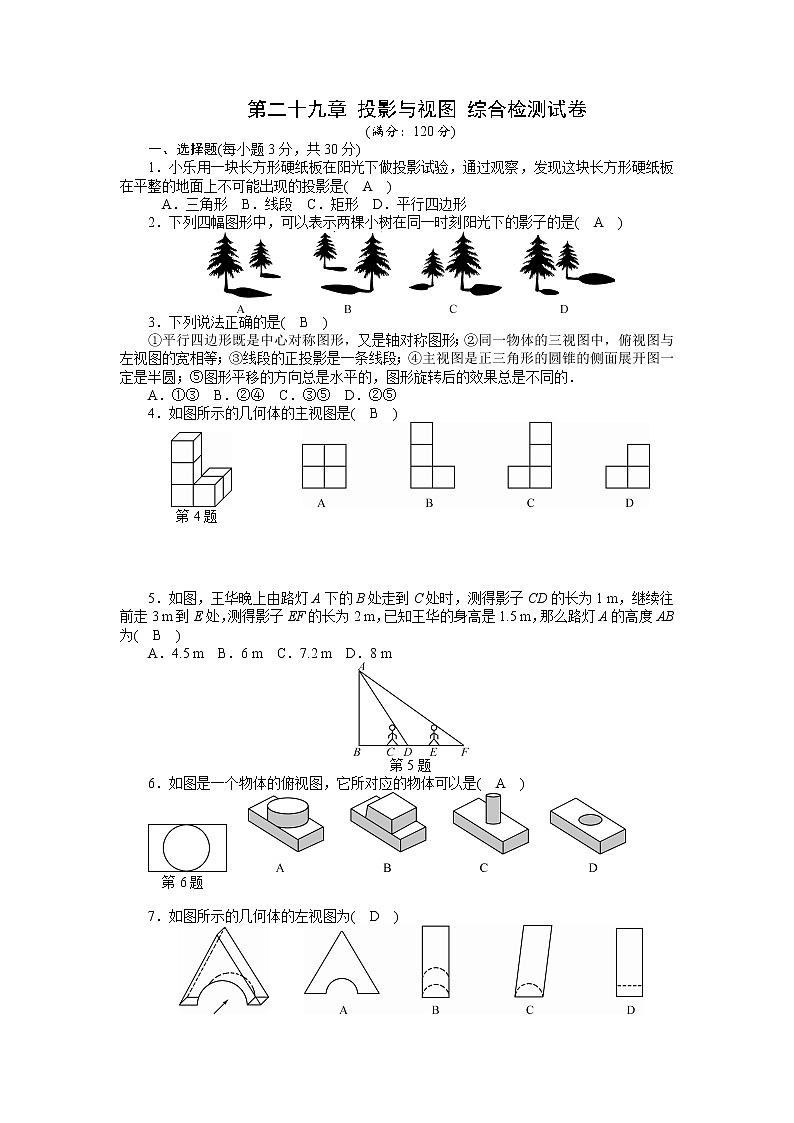
1．小乐用一块长方形硬纸板在阳光下做投影试验，通过观察，发现这块长方形硬纸板在平整的地面上不可能出现的投影是(　A　)

　A．三角形  B．线段  C．矩形  D．平行四边形

2．下列四幅图形中，可以表示两棵小树在同一时刻阳光下的影子的是(　A　)

3．下列说法正确的是(　B　)

①平行四边形既是中心对称图形，又是轴对称图形；②同一物体的三视图中，俯视图与左视图的宽相等；③线段的正投影是一条线段；④主视图是正三角形的圆锥的侧面展开图一定是半圆；⑤图形平移的方向总是水平的，图形旋转后的效果总是不同的．

A．①③  B．②④  C．③⑤  D．②⑤

4．如图所示的几何体的主视图是(　B　)

第4题

5．如图，王华晚上由路灯A下的B处走到C处时，测得影子CD的长为1 m，继续往前走3 m到E处，测得影子EF的长为2 m，已知王华的身高是1.5 m，那么路灯A的高度AB为(　B　)

A．4.5 m  B．6 m  C．7.2 m  D．8 m

第5题

6．如图是一个物体的俯视图，它所对应的物体可以是(　A　)

第6题

7．如图所示的几何体的左视图为(　D　)

第7题

8．如图所示的是由几个小立方体所搭成的几何体的俯视图，小正方形中的数字表示在该位置上的小立方体的个数，这个几何体的主视图是(　D　)

第8题

9．长方体的主视图与左视图如图所示(单位：cm)，则其俯视图的面积是(　A　)

A．12 cm2  B．8 cm2  C．6 cm2  D．4 cm2

第9题

10．如图是某天四个时刻的某一旗杆及其投影，若按从早到晚的时间顺序进行排列，则正确的排列顺序为(　B　)

第10题

A．①②③④  B．①④③②  C．②③④①  D．③②④①

二、填空题(每小题3分，共18分)

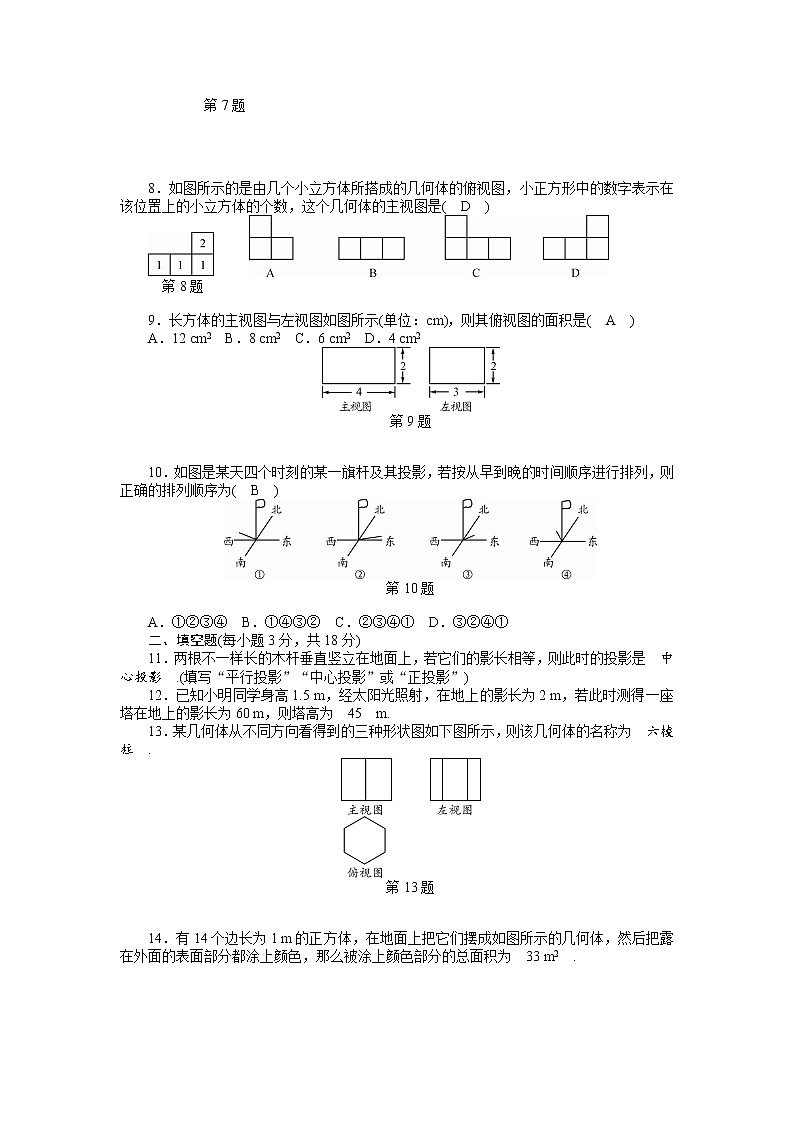
11．两根不一样长的木杆垂直竖立在地面上，若它们的影长相等，则此时的投影是　中心投影　.(填写“平行投影”“中心投影”或“正投影”)

12．已知小明同学身高1.5 m，经太阳光照射，在地上的影长为2 m，若此时测得一座塔在地上的影长为60 m，则塔高为　45　m.

13．某几何体从不同方向看得到的三种形状图如下图所示，则该几何体的名称为　六棱柱　.

第13题

14．有14个边长为1 m的正方体，在地面上把它们摆成如图所示的几何体，然后把露在外面的表面部分都涂上颜色，那么被涂上颜色部分的总面积为　33 m2　.

第14题

15．如图所示的是由一些小立方体所搭几何体的三视图，若在所搭几何体的基础上(不改变原几何体中小立方体的位置)，继续添加相同的小立方体，以搭成一个大正方体，至少还需要　54　个小立方体．

第15题

16．如图是某立体图形的三视图，则这个立体图形的侧面展开图的面积是　65π　.(结果保留π)

第16题

三、解答题(共72分)

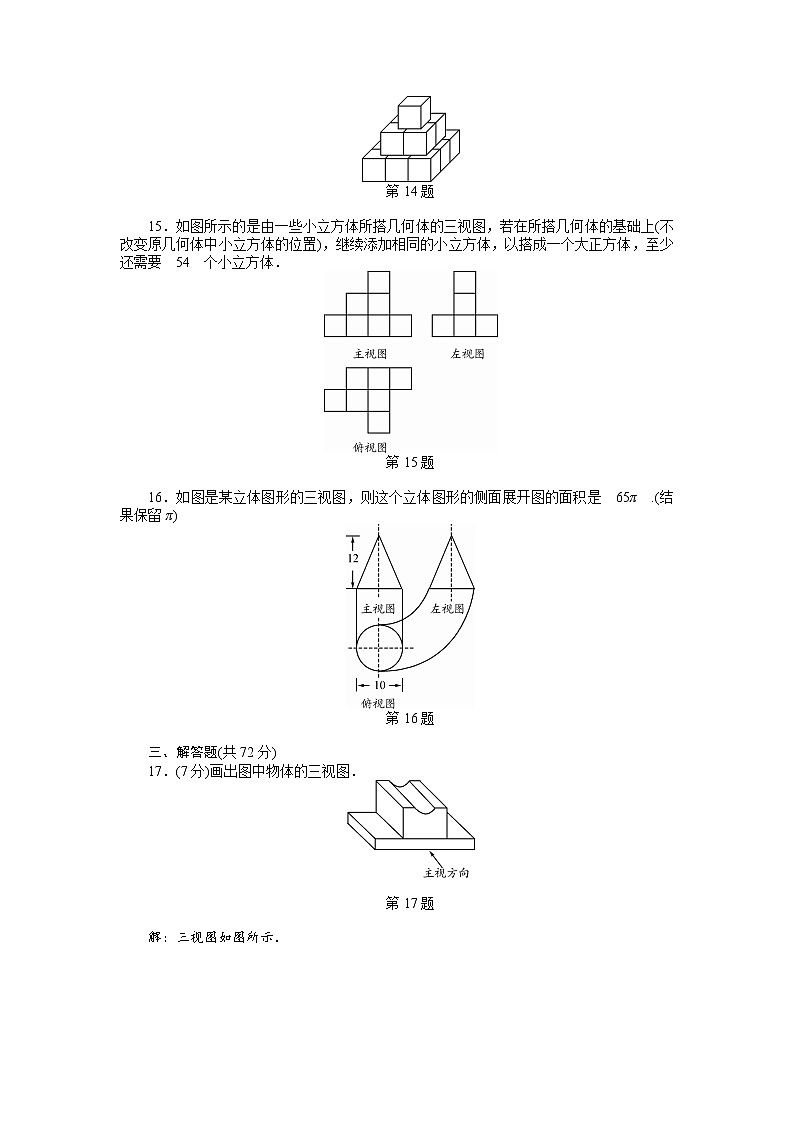
17．(7分)画出图中物体的三视图．

第17题

解：三视图如图所示．

18．(7分)如图，分别是两根木棒及其影子的情形．

第18题

(1)哪个图反映了太阳光下的情形？哪个图反映了路灯下的情形？

(2)在太阳光下，已知小明的身高是1.8米，影长是1.2米，旗杆的影长是4米，求旗杆的高；

(3)请在图中分别画出表示第三根木棒的影长的线段．

解：(1)图2反映了太阳光下的情形，图1反映了路灯下的情形．

(2)设旗杆的高为x米．根据题意，得＝，解得x＝6.故旗杆的高为6米．　(3)如图1中，FG为在路灯下的第三根木棒的影长；如图2，FG为在太阳光下的第三根木棒的影长．

图1

图2

19．(8分)如图所示的为某住宅区内的两幢楼，它们的高AB＝CD＝30 m，两楼间的距离AC＝24 m，现需了解甲楼对乙楼采光的影响情况．当太阳光与水平线的夹角为30°时，求甲楼的影子在乙楼上有多高．

第19题

解：如图，过点B作BF交CD于点F，过点F作FE⊥AB于点E.∵太阳光与水平线的夹角为30°，∴∠BFE＝30°.∵AC＝EF＝24 m，∴BE＝EF·tan 30°＝24×＝8(m)，∴FC＝CD－BE＝(30－8) m．即甲楼的影子在乙楼上的高度为(30－8)m.

20．(8分)如图是一个几何体的两个视图，求该几何体的体积．(π取3.14)

第20题

解：由图知，该几何体为一个下面是一个长方体，上面是一个圆柱体的组合体，其中长方体的长为30 cm，宽为25 cm，高为40 cm，圆柱体的底面直径为20 cm，高为32 cm，所以该几何体的体积V几何体＝V长方体＋V圆柱体＝30×25×40＋π×(20÷2)2×32≈40 048(cm3)．故该几何体的体积约为40 048 cm3.

21．(10分)由一些大小相同的小正方体组成的几何体的主视图和俯视图如图所示．

(1)请画出这个几何体的两种左视图；

(2)若组成这个几何体的小正方体的块数为n，请你写出n的所有可能的结果．

第21题

解：(1)如图所示(答案不唯一)．

(2)n可能为8或9或10或11.

22．(10分)如图是一个几何体的三视图．(单位cm)

(1)写出这个几何体的名称；

(2)根据所示数据计算这个几何体的表面积；

(3)如果一只蚂蚁要从这个几何体中的点B出发，沿表面爬到AC的中点D，请你求出最短路程．

第22题

解：(1)圆锥．　(2)表面积S＝S侧＋S底＝πrl＋πr2＝12π＋4π＝16π(cm2)．　(3)如图，将圆锥侧面展开，连接BB′交AC于点O.设∠BAB′＝n°.由题意，得4π＝，解得n＝120，∴∠BAB′＝120°.又∵点C为弧BB′的中点，∴∠B′AC＝∠BAC＝60°.∵AB＝AB′，∴∠AB′O＝∠ABO＝30°，∴∠AOB′＝∠AOB＝90°，∴AO＝AB＝3 cm，∴点O与点D重合．故BD为所求的最短路程，且BD＝AB·sin 60°＝3cm.

23．(10分)如图所示，王华在晚上由路灯A走向路灯B，当他走到点P时，发现身后他影子的顶部刚好接触到路灯A的底部，当他向前再步行12 m到达点Q时，发现身前他影子的顶部刚好接触路灯B的底部．已知王华的身高是1.6 m，两个路灯的高度都是9.6 m，且AP＝QB＝x m.

(1)求两个路灯之间的距离；

(2)当王华走到路灯B时，他在路灯A下的影长是多少？

第23题

解：(1)由题意，得△BQC∽△BAD，∴＝，即＝，∴＝，解得x＝3.∴AB＝2x＋12＝18 m．即两个路灯之间的距离是18 m.

(2)当王华走到路灯B处时(如图所示)，△EBF∽△EAD，∴＝，即＝，∴＝，解得BE＝3.6 m．即王华走到路灯B时，他在路灯A下的影长是3.6 m.

24．(12分)某生活小区为了改善居民的居住环境，把一部分平房拆除后准备建几栋楼房，由于某种原因，最北边的一排平房暂时没拆．如图，建筑工人准备在距离平房55米的地方(平房的南边)打地基建甲楼，已知甲楼预计34米高，平房的窗台高1.2米，该地区冬天中午12时阳光从正南方照射时，光线与水平线的最小夹角为30°.

(1)甲楼是否会挡住平房的采光？为什么？

(2)假设在甲楼南边再建一栋同样高度的乙楼，那么甲、乙两楼之间的距离至少为多少米才不影响甲楼采光？(已知甲楼1楼的窗台高1.6米，结果精确到0.01米)

第24题

解：(1)会．理由如下：过点C作CE⊥BD于点E，则CE＝AB＝55米．∵阳光入射角为30°，∴∠DCE＝30°.在Rt△DCE中，∵tan∠DCE＝，∴DE＝CE·tan∠DCE＝55·tan 30°≈31.75(米)．∵34＞31.75＋1.2，∴甲楼会挡住平房的采光．　(2)过点F作FQ⊥HG于点Q.∵阳光入射角为30°，∴∠HFQ＝30°.在Rt△HFQ中，∵tan∠HFQ＝，∴FQ＝＝≈56.12(米)，∴甲、乙两楼之间的楼距至少应为56.12米才不影响甲楼采光．