人教版5.1.3 同位角、内错角、同旁内角精品课件ppt

这是一份人教版5.1.3 同位角、内错角、同旁内角精品课件ppt，共59页。PPT课件主要包含了同位角，内错角，同旁内角，同旁内，错因分析，基础巩固，综合运用，解1如图，复习巩固，拓广探索等内容，欢迎下载使用。

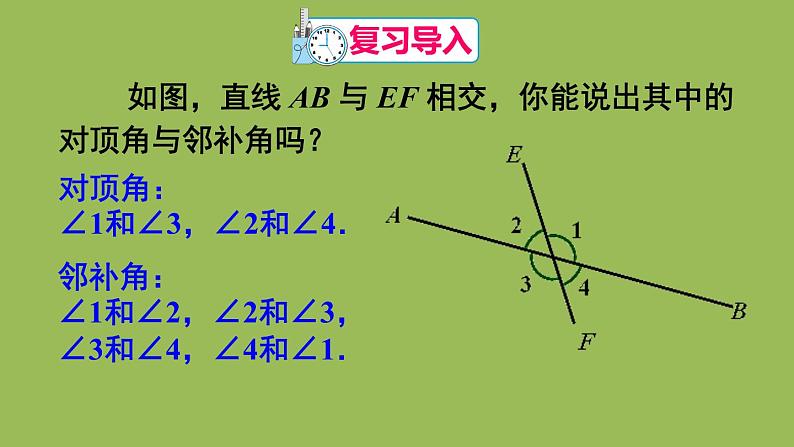
如图，直线 AB 与 EF 相交，你能说出其中的对顶角与邻补角吗？
对顶角：∠1和∠3，∠2和∠4．
邻补角：∠1和∠2，∠2和∠3，∠3和∠4，∠4和∠1．
学习目标： 1．能说出同位角、内错角、同旁内角的概念. 2．能结合图形正确找出同位角、内错角、同旁内角.
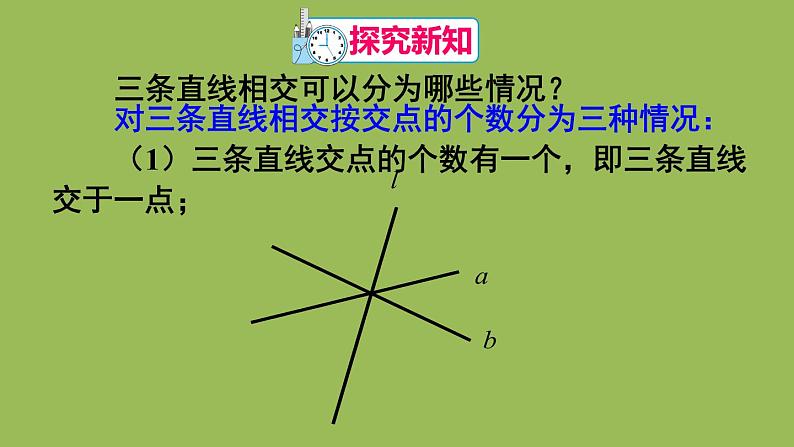
三条直线相交可以分为哪些情况？
对三条直线相交按交点的个数分为三种情况：
（1）三条直线交点的个数有一个，即三条直线交于一点；
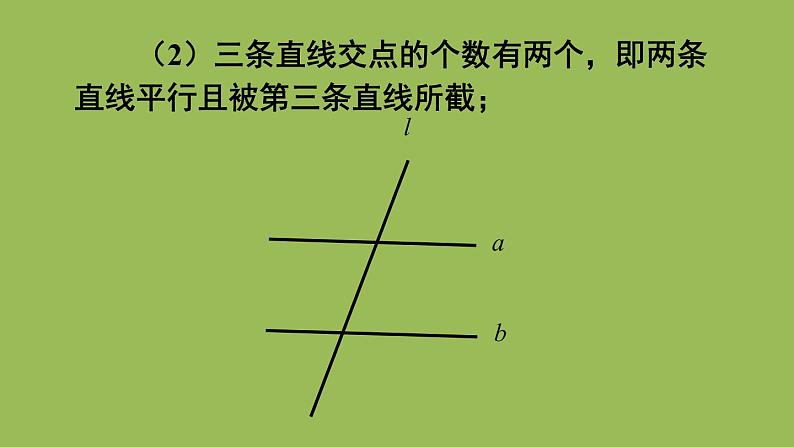
（2）三条直线交点的个数有两个，即两条直线平行且被第三条直线所截；
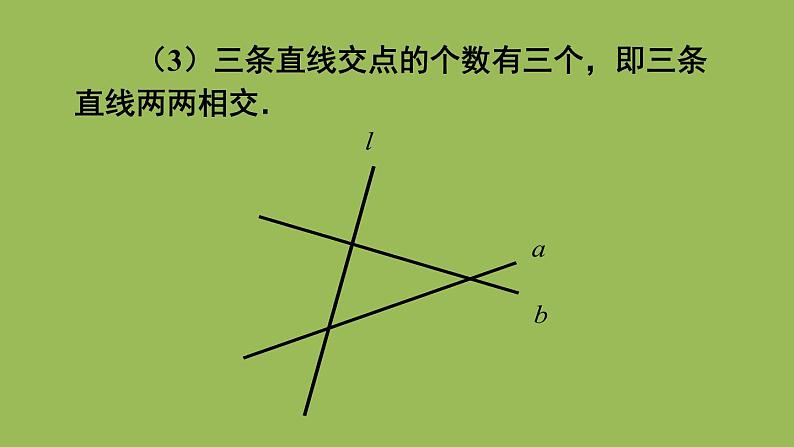
（3）三条直线交点的个数有三个，即三条直线两两相交．
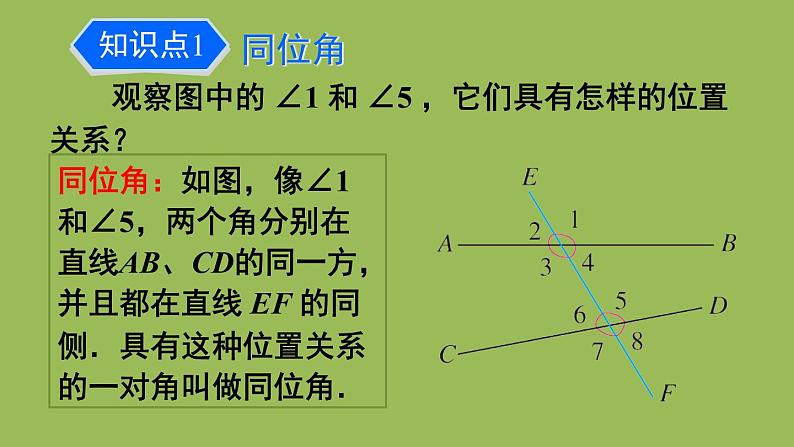
观察图中的 ∠1 和 ∠5 ，它们具有怎样的位置关系？
同位角：如图，像∠1和∠5，两个角分别在直线AB、CD的同一方，并且都在直线 EF 的同侧．具有这种位置关系的一对角叫做同位角．
（1）你能找出图中还有哪几对角构成同位角？（2）两条直线被第三条直线所截构成的八个角中，共有几对同位角？
（1）除了∠1 和∠5是同位角，还有∠2 和∠6，∠3 和∠7， ∠4 和∠8 也构成同位角．
（2）共有 4 对同位角．
观察图中的 ∠3 和 ∠5 ，它们有怎样的位置关系？
内错角：如图，像∠3 和∠5，两个角都在直线 AB、CD 之间，并且分别在直线 EF 两侧．具有这种位置关系的一对角叫做内错角．
（1）你能找出图中还有哪几对角构成内错角？（2）两条直线被第三条直线所截构成的八个角中，共有几对内错角？
（1）除了∠3 和∠5是内错角，还有∠4 和∠6 也构成内错角．
（2）共有 2 对内错角．
如图，我们称∠3 和∠6 为同旁内角，你能根据两个角的特征，描述一下同旁内角的定义吗？
同旁内角：如图，像∠3和∠6，两个角都在直线AB、CD 之间，并且都在直线 EF 的同一旁．具有这种位置关系的一对角叫做同旁内角．
（1）你能找出图中还有哪几对角构成同旁内角？（2）两条直线被第三条直线所截构成的八个角中，共有几对同旁内角？
（1）除了∠3 和∠6是同旁内角，还有∠4 和∠5 也构成同旁内角．
（2）共有 2 对同旁内角．
例 如图，直线 DE、BC 被直线 AB 所截，（1）∠1 和∠2，∠1 和∠3，∠1 和∠4 各是什么位置关系的角？
∠1 与 ∠2 是内错角，∠1 与∠3 是同旁内角，∠1 与∠4 是同位角．
如果∠1＝∠4，由对顶角相等，得∠2＝∠4，那么∠1=∠2.
因为∠4 和∠3 互补，得∠4 + ∠3=180º，又因为∠1 =∠4， 所以∠1 +∠3 = 180º，即∠1 和∠3 互补．
例 如图，直线 DE、BC 被直线 AB 所截，（2）如果∠1＝∠4，那么∠1 和∠2 相等吗？∠1 和∠3 互补吗？为什么？
1.分别指出下列图中的同位角、内错角、同旁内角．
同位角：∠2 与∠6，∠4 与∠8，∠3 与∠7，∠1 与∠5内错角：∠3 与∠6，∠4 与∠5同旁内角：∠3 与∠5，∠4 与∠6
同位角：∠1 与∠3，∠2 与∠4．内错角：无．同旁内角：∠2 与 ∠3．
2. 如图，∠B 与哪个角是内错角，与哪个角是同旁内角？它们分别是哪两条直线被哪一条直线所截形成的？对∠C 进行同样的讨论.
解：∠B 与∠DAB 是内错角，与∠BAE 是同旁内角，它们都是由 DE 与 BC 被 AB 所截形成的，还与∠BAC 是同旁内角，它们是由 AC、BC 被 BA 所截形成的. ∠C 与∠EAC 是内错角，与∠DAC 是同旁内角，它们都是由 DE 与 BC 被 AC 所截形成的. 还与∠BAC 是同旁内角，它们是由 AB、BC 被 AC 所截形成的.
1.如图，∠2 与∠3 是_______角，∠2 和∠4是_______角，∠2 与∠5 是_______角，∠2 与∠8是_______角，∠2 与∠6 是________角.
2. 如图：①∠DAE 的同位角是______，它们是直线______和直线______被直线______所截形成的.②∠CAD 的内错角是______，它们是直线______和直线______被直线______所截形成的.
∠DAB，∠CAB，∠C
③∠B 的同旁内角有______________________.
1.如图，所标出的 7 个角中共有____对内错角，____对同位角，____对同旁内角.
误区一 对同位角、内错角、同旁内角的定义理解不透彻
两条直线被第三条直线所截，这是判断同位角、内错角、同旁内角的前提条件，解答此题时，常常误认为∠4和∠6是同位角，∠3和∠5是同位角，∠4和∠7是内错角等，事实上这三对角中的每一对角都没有公共边.
2. 如图，∠1 与∠2，∠3 与∠4分别是内错角，它们分别是由哪两条直线被哪一条直线所截得到的？
误区二 由角反推三线时出错
错解中没有分清∠1 与 ∠2，∠3 与∠4分别是由哪两条直线被第三条直线所截得到的，而导致错误. 应根据相关的概念来确定.
1.如图，直线 a、b 被直线 c 所截，∠1 和∠2是________角，∠3 和∠4 是_________角，∠2 和∠3 是________角.
2.如图，已知∠1 和∠2 是内错角，则下列表述正确的是（ ）A.∠1 和∠2 是由直线AD、AC被CE所截形成的B.∠1 和∠2 是由直线AD、AC被BD所截形成的C.∠1 和∠2 是由直线DA、DB被CE所截形成的D.∠1 和∠2 是由直线DA、DB被AC所截形成的
3.如图，∠1 和∠2，∠3 和∠4 是由哪两条直线被一条直线所截形成的？它们各是什么位置关系的角？
（1） （2）
解：（1）∠1 和 ∠2 是由直线 DC、AB 被 BD 所截形成的内错角，∠3 和∠4 是由直线 AD、BC 被 BD 所截形成的内错角.
（2）∠1 和 ∠2 是由直线 AB、CD 被 BC 所截形成的同旁内角.∠3 和 ∠4 是由直线 AD、BC 被 AE 所截形成的同位角.
1．你能总结一下同位角、内错角、同旁内角分别具有哪些特征吗？2．你认为在图形中识别同位角、内错角、同旁内角的关键是什么？
直线 AB，CD 相交于点 O .（1）OE、OF 分别是∠AOC、∠BOD 的平分线，画出这个图形；（2）射线 OE、OF 在同一条直线上吗？（3）画出∠AOD 的平分线 OG，OE 与 OG 有怎样的位置关系？为什么？
（2）射线 OE、OF 在同一条直线上.
OE⊥OG .因为OE平分∠AOC，所以∠AOE = ∠AOC.同理：∠AOG = ∠AOD .所以∠AOE + ∠AOG = （∠AOC +∠AOD）= ×180°= 90°.所以OE⊥OG .
1. 从课后习题中选取；2. 完成练习册本课时的习题.
1.下列各图中，∠1 和∠2 是不是对项角？
解：（1）、（3）、（4）中的∠1 与∠2 不是对顶角；（2）中的∠1 与∠2 是对顶角.
2. 如图，直线 AB，CD，EF 相交于点 O.（1）写出∠AOC，∠BOE 的邻补角；（2）写出∠DOA，∠EOC 的对顶角；（3）如果∠AOC = 50°，求∠BOD，∠COB的度数.
解：（1）∠AOC 的邻补角是 ∠AOD、∠COB；∠BOE 的邻补角是 ∠AOE、∠BOF；（2）∠DOA 的对顶角是 ∠BOC；∠EOC 的对顶角是 ∠DOF；
（3）因为∠BOD 与∠AOC 是对顶角，所以∠BOD =∠AOC = 50°.因为∠COB 与∠AOC 互为邻补角，所以∠COB +∠AOC = 180°.则∠COB = 180°-∠AOC = 180°-50°= 130°.
3. 找出图中互相垂直的线段，并用三角尺检验.
解：OA⊥OC，OB⊥OD.
4. 如图，在一张半透明的纸上画一条直线 l ，在 l 上任取一点 P，在 l 外任取一点 Q，折出过点P 且与 l 垂直的直线.这样的直线能折出几条？为什么？过点 Q 呢？
解：过点 P 且与 l 垂直的直线只能折出一条，因为过一点有且只有一条直线与已知直线垂直.过点 Q 且与 l 垂直的直线也只能折出一条， 理由同上.
5. 如图，直线 AB，CD 相交于点 O，EO ⊥ AB，垂足为 O，∠EOC = 35°.求∠AOD 的度数.
解：因为EO⊥AB，所以∠AOE = 90°，所以∠AOC +∠EOC =∠AOE = 90°，
所以∠AOC = 90°-∠EOC = 90°-35°= 55°，又因为∠AOC +∠AOD = 180°，所以∠AOD = 180°-∠AOC = 125°.
6. 如图，画 AE⊥BC，CF⊥AD，垂足分别为E，F.
解：AE 和 CF 如图中虚线所示.
7. 如图，用量角器画∠AOB 的平分线 OC，在 OC 上任取一点，比较点 P 到 OA，OB 的距离的大小.
解：∠AOB 的平分线 OC 如图中虚线所示；P 到 OA、OB 的距离相等.
8. 如图，直线 AB，CD 相交于点 O，OA 平分∠EOC.（1）若∠EOC = 70°，求∠BOD 的度数；（2）若∠EOC∶∠EOD = 2∶3，求∠BOD 的度数.
解：（1）因为 OA 平分∠EOC 且∠EOC = 70°，所以∠AOC = ∠EOC = ×70°= 35°.因为直线 AB、CD 相交于点 O，所以∠BOD 与∠AOC 是对顶角. 故∠BOD = ∠AOC = 35°.
（2）因为∠EOC∶∠EOD = 2∶3，又因为∠EOC +∠EOD = 180°，所以∠EOC = 180°× = 72°，因为 OA 平分∠EOC，所以∠AOC = ∠EOC =36°，所以∠BOD =∠AOC = 36°.
9. 图中是对顶角量角器，你能说出用它测量角的原理吗？
解：对顶角的性质定理：对顶角相等.
10. 如图，这是小明同学在体育课上跳远后留下的脚印，他的跳远成绩是多少（比例尺为1∶150）？
解：经测量起跳线到右脚后跟的距离为 2.5 cm，设小明实际跳了 x cm，依题意，得2.5∶x = 1∶150，x = 375.因为 375 cm = 3.75 m.所以小明的跳远成绩是 3.75 m.
11. 如图，∠1 和∠2，∠3 和∠4 各是哪两条直线被哪一条直线所截形成的？它们各是什么位置关系的角？
解：（1）∠1 和∠2 是直线 AB、CD 被直线BD 所截形成的，是内错角；∠3 和∠4 是直线 AD、BC 被直线 BD 所截形成的，是内错角.
（2）∠1 和∠2 是直线 AB、CD 被直线 BC 所截形成的，是同旁内角；∠3 和∠4 是直线 AD、BC 被直线 AE 所截形成的，是同位角.
12. 如图，AB⊥l ，BC⊥l ，B 为垂足，那么A，B，C 三点在同一条直线吗？
解：A、B、C 三点在同一条直线上. 因为过一点 B 有且只有一条直线与 l 垂直.
13.直线 AB，CD 相交于点 O.（1）OE，OF 分别是∠AOC，∠BOD 的平分线. 画出这个图形.（2）射线 OE，OF 在同一条直线上吗？（3）画∠AOD 的平分线 OG. OE 与 OG 有什么位置关系？
（2）射线 OE、OF 在同一条直线上.理由如下：由角的平分线定义可知∠COE = ∠AOC，∠DOF = ∠DOB.由对顶角相等，可得∠AOC =∠DOB，所以∠COE =∠DOF.
由平角的定义，可知∠COD = 180°，即∠EOC +∠EOD = 180°.所以∠DOF + ∠EOD = 180°，即∠EOF = 180°，所以射线 OE、OF 在同一条直线上.