苏教版 (2019)必修 第二册10.2 二倍角的三角函数优质ppt课件

这是一份苏教版 (2019)必修 第二册10.2 二倍角的三角函数优质ppt课件，共51页。PPT课件主要包含了必备知识·自主学习，关键能力·合作学习，课堂检测·素养达标等内容，欢迎下载使用。

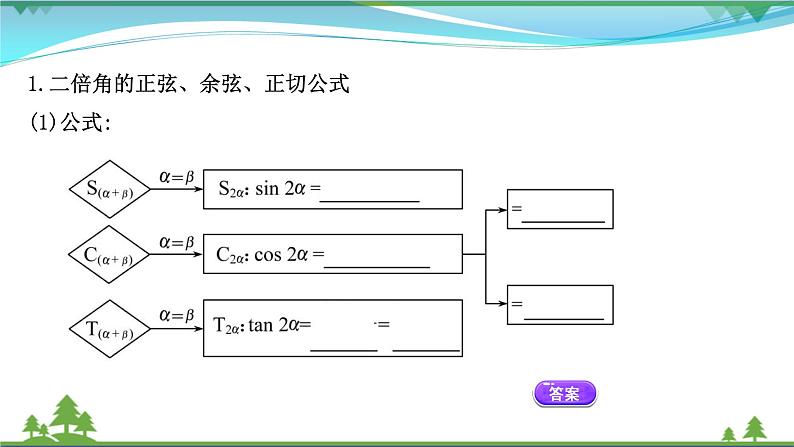
1.二倍角的正弦、余弦、正切公式(1)公式:
(2)本质:两角和的正弦、余弦、正切公式,当两角相等时的特殊形式.(3)应用:①化简;②求值;③证明.
【思考】(1)所谓的“二倍角”公式,一定是角α与2α之间的转化关系吗?为什么?提示:不一定.对于“二倍角”应该广义的理解,如:8α是4α的二倍角,3α是 α的二倍角,α是 的二倍角, 是 的二倍角,…,这里蕴含着换元思想.这就是说“倍”是相对而言的,是描述两个数量之间关系的.
(2)公式中的角α是任意角吗?提示:对于公式S2α、C2α中的角α是任意角,但是T2α中的角α要保证tan 2α,tan α有意义且分母1-tan2α≠0.
2.倍角公式的变换(1)因式分解变换cs 2α=cs2α-sin2α=(cs α+sin α)(cs α-sin α).(2)配方变换1±sin 2α=sin2α+cs2α±2sin αcs α=(sin α±cs α)2.
(3)升幂缩角变换1+cs 2α=2cs2α,1-cs 2α=2sin2α.(4)降幂扩角变换cs2α= (1+cs 2α),sin2α= (1-cs 2α),sinαcs α= sin 2α.
【基础小测】1.辨析记忆(对的打“√”,错的打“×”)(1)倍角的正切公式的适用范围不是任意角.(　　)(2)对于任意的角α,都有sin 2α=2sin α成立.(　　)(3)存在角α,使cs 2α=2cs α成立.(　　)(4)cs 3αsin 3α= sin 6α对任意的角α都成立.(　　)
提示:(1)√.倍角的正切公式,要求α≠ +kπ(k∈Z)且α≠± +kπ(k∈Z),故此说法正确.(2)×.当α= 时,sin 2α=sin = ,而2sin α=2× =1.(3)√.由cs 2α=2cs α=2cs2α-1,得cs α= 时,cs 2α=2cs α成立.(4)√.由倍角的正弦公式可得.
2.sin 15°sin 75°的值为(　　) 【解析】选B.原式=sin 15°cs 15°= sin 30°= .
3.(教材二次开发:例题改编)已知cs α=- ,α∈ ,则sin 2α=________,cs 2α=________,tan 2α=________. 【解析】因为cs α=- ,α∈ ,所以sin α=- ,所以sin 2α=2sin αcs α= ,cs 2α=2cs2α-1= ,tan 2α= 答案: 　 　
类型一　给角求值问题(数学运算)【题组训练】1. =(　　)A. 　　　B. 　　　C.1　　　D.-12. = (　　)A.1B.2C. D.-13. -cs2 =________. 
【解析】1.选A.原式= 2.选B. 3.原式= 答案:-
【解题策略】利用二倍角公式解决给角求值问题的策略(1)注意观察式子的结构特点及角之间是否存在特殊的倍数关系,灵活正用或逆用二倍角公式.(2)结合诱导公式恰当变化函数名称,灵活处理系数,构造二倍角公式的形式.
【补偿训练】求下列各式的值:(1) (2)1-2sin2750°;(3)
【解析】(1)原式= (2)原式=cs(2×750°)=cs 1 500°=cs(4×360°+60°)=cs 60°= .(3)原式=tan(2×150°)=tan 300°=tan(360°-60°)=-tan 60°=- .
类型二　条件求值问题(数学运算)【典例】已知 求cs 的值.
【解题策略】解决条件求值问题的方法(1)将已知式或未知式化简,使关系明朗化;(2)寻找角之间的关系,特别是已知角与要求的角之间的二倍关系,如果二倍关系中含有已知角和某些特殊角,则利用诱导公式转化后整体代入.
【跟踪训练】已知tan α+ = ,α∈ ,求cs 2α和sin 的值.
【解析】由tan α+ 则 ,即sin 2α= .因为α∈ ,所以2α∈ ,所以cs 2α= sin =sin 2α·cs +cs 2α·sin =
【补偿训练】已知α∈ ,且sin 2α=sin 求α.
【解析】因为sin 2α=-cs 所以原式可化为1-2cs2
解得cs =1或cs =- .因为α∈ ,所以α+ ∈ ,故α+ =0或α+ = ,即α=- 或α= .
类型三　化简、证明问题(数学运算、逻辑推理)角度1　化简问题 【典例】化简:(1) 【思路导引】结合题目特点,利用二倍角的正弦、余弦公式化简.
【解析】(1)原式= (2)原式= =|sin 10°+cs 10°|+|sin 10°-cs 10°|=sin 10°+cs 10°+cs 10°-sin 10°=2cs 10°.
【变式探究】本例(2)若改为: ,试化简.【解析】原式=
角度2　证明问题 【典例】证明 【思路导引】利用二倍角公式化简左边式子求解.【解析】
【解题策略】1.化简三角函数式的常用方法(1)切化弦;(2)异名化同名;(3)异角化同角;(4)高次降低次.2.化简三角函数式的常用技巧(1)特殊角的三角函数与特殊值的互化;(2)对于分式形式,应分别对分子、分母进行变形处理,有公因式的提取公因式后进行约分;(3)对于二次根式,注意倍角公式的逆用;(4)利用角与角之间的隐含关系,如互余、互补等.
3.证明问题的原则及一般步骤(1)观察式子两端的结构形式,一般是从复杂到简单,如果两端都比较复杂,就将两端都化简,即采用“两头凑”的思想.(2)证明的一般步骤是:先观察,找出角、函数名称、式子结构等方面的差异,然后本着“复角化单角”“异名化同名”“变量集中”等原则,设法消除差异,达到证明的目的.
【题组训练】1.cs4 -sin4 的化简结果为(　　)　　　　　　　　A.cs B.cs αC.cs 2αD.cs 4α【解析】选B.cs4 -sin4 = =cs α.
2.求证:cs2θ(1-tan2θ)=cs 2θ.【证明】方法一:左边=cs2θ =cs2θ-sin2θ=cs 2θ=右边,得证.方法二:右边=cs 2θ=cs2θ-sin2θ=cs2θ =cs2θ(1-tan2θ)=左边,得证.
3.化简: ,其中θ∈(0,π).
【解析】原式= ①当θ∈ 时, ∈ ,cs ≥sin ,此时原式=sin +cs -cs +sin =2sin .②当θ∈ 时, ∈ ,cs 类型四　倍角公式与三角函数性质的综合(逻辑推理、数学运算)【典例】求函数f(x)=5 cs2x+ sin2x-4sin xcs x,x∈ 的最小值,并求其单调减区间.【思路导引】化简f(x)的解析式→f(x)=Asin(ωx+φ)+B→ωx+φ的范围→求最小值,单调减区间
【解析】f(x)=5 · + · -2sin 2x=3 +2 cs2x-2sin2x=3 +4 =3 +4 =3 +4sin =3 -4sin ,
因为 所以 所以sin 所以当2x- 即x= 时,f(x)取最小值为 因为y=sin 在 上单调递增,所以f(x)在 上单调递减.
【解题策略】倍角公式与三角函数性质的综合问题的解题策略运用三角函数的和、差、倍角公式将函数关系式化成y=asin ωx+bcs ωx+k的形式,借助辅助角公式化为y=Asin(ωx+φ)+k(或y=Acs(ωx+φ)+k)的形式,将ωx+φ看作一个整体研究函数的性质.
【跟踪训练】求函数y=sin4x+2 sin xcs x-cs4 x的最小正周期和最小值,并写出该函数在[0,π]上的单调递减区间.
【解析】 y=sin4x+2 sin xcs x-cs4x=(sin2x+cs2x)(sin2x-cs2x)+2 sin xcs x=-cs 2x+ sin 2x所以T= =π,ymin=-2.由2kπ+ ≤2x- ≤2kπ+ ,k∈Z,得kπ+ ≤x≤kπ+ ,k∈Z,又x∈[0,π],所以令k=0,得函数的单调递减区间为
1.已知sin x= ,则cs 2x的值为(　　)　　　　　 【解析】选A.因为sin x= ,所以cs 2x=1-2sin2 x=1-2×
2.计算1-2sin222.5°的结果为(　　) 【解析】选B.1-2sin222.5°=cs 45°= .
【补偿训练】　　　sin 105°cs 105°的值为(　　) 【解析】选B.sin105°cs 105°= sin210°= sin(180°+30°)=- sin30°=- .
3.已知cs α= ,则cs 2α等于________. 【解析】由cs α= 得cs2α=2cs2α-1=2× 答案:-
4.函数f(x)=sin -2 ·sin2x的最小正周期是________. 【解析】f(x)=sin -2 sin2x= sin 2x- cs 2x-2 × = sin 2x+ cs 2x- =sin - ,故最小正周期为π.答案:π