人教版七年级下册6.3 实数优秀课件ppt

这是一份人教版七年级下册6.3 实数优秀课件ppt，共32页。PPT课件主要包含了知识梳理，算术平方根，表示方法，平方根，开平方，平方根的性质，立方根，开立方，的立方根是0，相反数等内容，欢迎下载使用。

一个正数有两个平方根，它们互为相反数
0 的算术平方根与平方根都是 0
负数没有算术平方根，也没有平方根
正数的立方根是一个正数
负数的立方根是一个负数
每一个实数都可以用数轴上的一个点来表示
数轴上的每一个点都表示一个实数
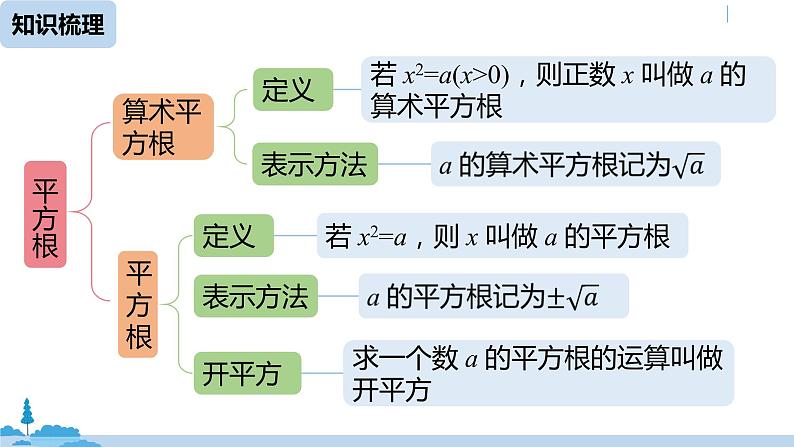
一般地，如果一个正数 x 的平方等于 a，即 x2=a，那么这个正数 x 叫做 a 的 .
(1)算术平方根的双重非负性
(2)算术平方根的估算
在估计有理数的算术平方根的过程中，为方便计算，可借助计算器求一个正有理数 a 的算术平方根(或其近似数).
(3)用计算器求算术平方根
平方根的性质：① 正数有两个平方根，两个平方根互为相反数；② 0 的平方根还是 0；③负数没有平方根.
一般地，如果一个数的平方等于 a，那么这个数叫做 a 的 或 .这就是说，如果 x2=a，那么 x 叫做 a 的平方根.
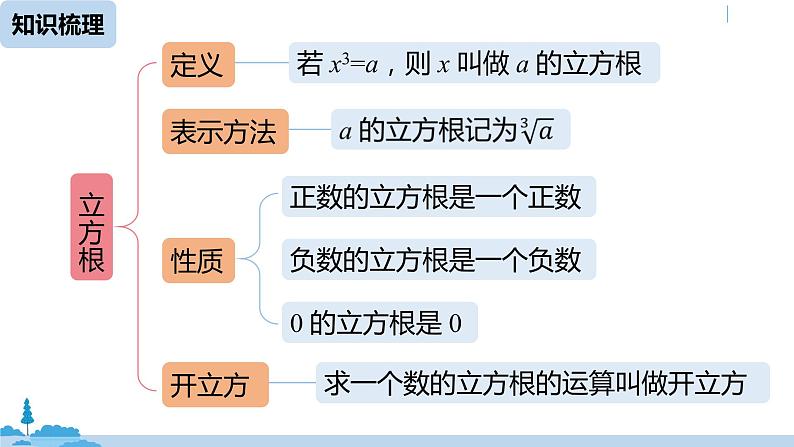
一般地，如果一个数的立方等于 a，那么这个数叫做 a 的 或 ．这就是说，如果 x3=a，那么 x 叫做 a 的立方根.
(1)立方根的性质：①正数的立方根是正数；② 0 的立方根是 0；③负数的立方根是负数.
(2)用计算器求立方根
无限不循环小数叫做_______；有理数和无理数统称为 .
每一个实数都可以用数轴上的一个点来表示；
反过来，数轴上的每一点都表示一个实数.
(2)实数和数轴上的点一 一对应.
①正数大于零，负数小于零，正数大于负数；②两个正数，绝对值大的数较大；③两个负数，绝对值大的数反而小.
相反数：数 a 的相反数是 -a，这里 a 表示任意一个实数.
绝对值：一个正实数的绝对值是它本身；一个负实数的绝对值是它的相反数；0 的绝对值是 0.设 a 表示一个实数，则
①在进行实数的运算时，有理数的运算法则及运算性质等同样适用.②当遇到无理数并且需要求出结果的近似值时，可以按照所要求的精确度用相应的近似有限小数去代替无理数，再进行计算.
负数没有平方根，但是有立方根
2.已知 2x+1 的平方根是±4，4x-8y +2的立方根是-2，求-10(x +y)的立方根.
解：由图可知 a<0，b<0，c>0，a>b，则 a-b>0，b-c<0，所以原式=|a|+|a-b|+a+b-|b-c|=-a+a-b+a+b-c+b=a+b-c.
2×3-(-6)=12