



2021年中考数学总复习 拉分题训练课件 多解问题探究题
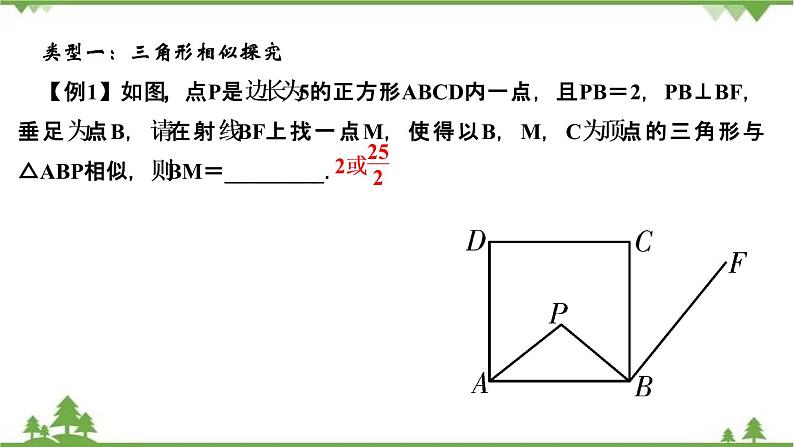
展开类型一:三角形相似探究【例1】如图,点P是边长为5的正方形ABCD内一点,且PB=2,PB⊥BF,垂足为点B,请在射线BF上找一点M,使得以B,M,C为顶点的三角形与△ABP相似,则BM=_________.
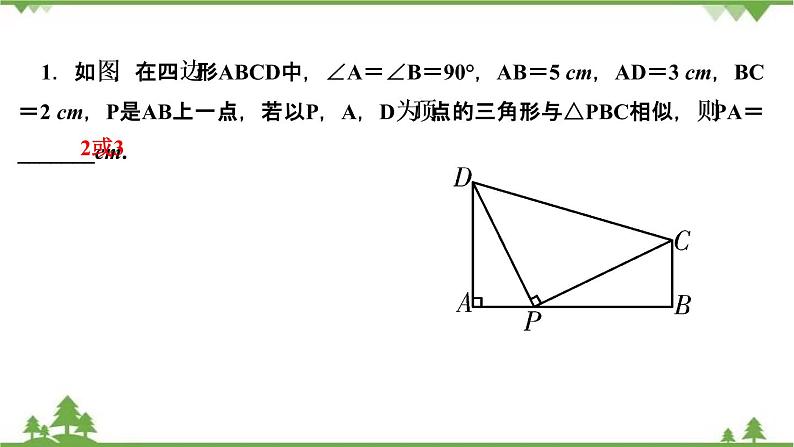
1.如图,在四边形ABCD中,∠A=∠B=90°,AB=5 cm,AD=3 cm,BC=2 cm,P是AB上一点,若以P,A,D为顶点的三角形与△PBC相似,则PA=_______cm.
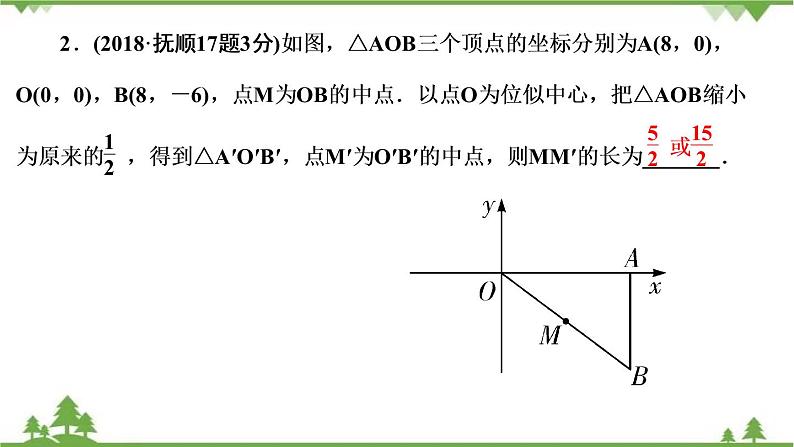
3.(2019·辽阳17题3分)如图,平面直角坐标系中,矩形ABOC的边BO,CO分别在x轴,y轴上,A点的坐标为(-8,6),点P在矩形ABOC的内部,点E在BO边上,满足△PBE∽△CBO,当△APC是等腰三角形时,P点坐标为______________________
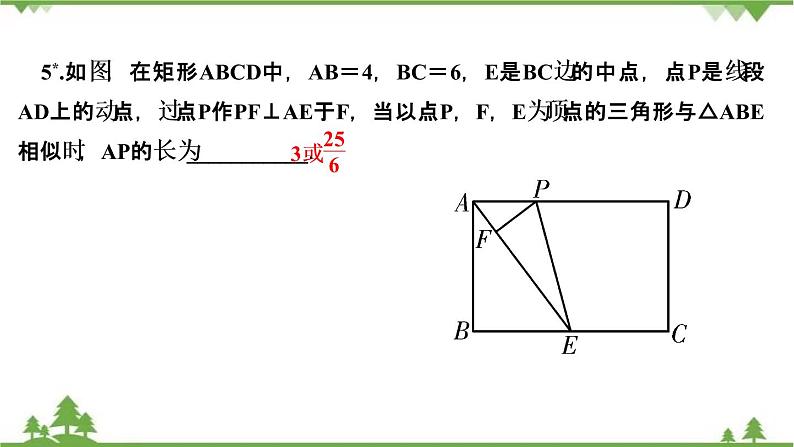
5*.如图,在矩形ABCD中,AB=4,BC=6,E是BC边的中点,点P是线段AD上的动点,过点P作PF⊥AE于F,当以点P,F,E为顶点的三角形与△ABE相似时,AP的长为___________.
6*.如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,点E,F分别在边BC,AC上,沿EF所在的直线折叠∠C,使点C的对应点D恰好落在边AB上,若△EFC和△ABC相似,则AD的长为________.
类型二:图形存在性探究 1.等腰三角形存在性【例2】(2020·沈阳16题3分)如图,在矩形ABCD中,AB=6,BC=8,对角线AC,BD相交于点O,点P为边AD上一动点,连接OP,以OP为折痕,将△AOP折叠,点A的对应点为点E,线段PE与OD相交于点F.若△PDF为直角三角形,则DP的长为_________.
2.直角三角形存在性【例3】*(沈阳模拟)在△ABC中,CO是AB边上的中线,∠AOC=60°,AB=2,点P是直线OC上的一个动点,则当△PAB为直角三角形时,边AP的长为______________.【例4】(2019·抚顺17题3分)如图,在Rt△ABC中,∠ACB=90°,CA=CB=2,D是△ABC所在平面内一点,以A,B,C,D为顶点的四边形是平行四边形,则BD的长为______________.
1*.(2020押题密卷)半径为5的⊙O是锐角△ABC的外接圆,AB=AC,连接OB,OC,延长CO交弦AB于点D.若△OBD是直角三角形,则弦BC的长为____________.2.一张直角三角形纸片ABC,∠ACB=90°,AB=10,AC=6,点D为BC边上的任一点,沿过点D的直线折叠,使直角顶点C落在斜边AB上的点E处,当△BDE是直角三角形时,则CD的长为____________.
3*.(辽阳模拟)如图,在等边三角形ABC中,AB=8,BD⊥AC于点D,点E,F分别是BC,DC上的动点,沿EF所在直线折叠△CEF,使点C落在BD上的点C′处,当△BEC′是直角三角形时,BC′的值为______________.
4*.如图,在矩形ABCD中,AB=4,BC=6,E是BC的中点,连接AE,P是边AD上一动点,沿过点P的直线将矩形折叠,使点D落在AE上的点D′处,当△APD′是直角三角形时,PD=________________.
5.如图,在△ABC中,∠A=90°,AB=3,AC=6,点D是AC边的中点,点P是BC边上一点,连接DP,若△BDP为等腰三角形,则线段BP的长为____________.
6*.在矩形ABCD中,AB=3,BC=4,点E,F分别为BC,AC上的两个动点,将△CEF沿EF折叠,点C的对应点为G,若点G落在射线AB上,且△AGF恰为直角三角形,则线段CF的长为_______________.
7*.(沈阳模拟)如图,在△ABC中,∠ACB=90°,AC=BC=2,D是边AC的中点,CE⊥BD于点E.若F是边AB上的点,且使△AEF为等腰三角形,则AF的长为________________.
类型三:特殊位置探究
5*.如图,在矩形ABCD中,AB=1,AD=2,点E是边AD上的一个动点,把△BAE沿BE折叠,点A落在A′处,如果A′恰在矩形的对称轴上,则AE的长为__________.
6*.如图,在菱形ABCD中,∠A=60°,AB=3,点M为AB边上一点,AM=2,点N为AD边上的一动点,沿MN将△AMN翻折,点A落在点P处,当点P在菱形的对角线上时,AN的长度为_________________.
7*.如图,在矩形ABCD中,点P为AD上一个动点,以PB 为对称轴将△APB折叠得到△EPB,点A的对称点为点E,射线BE交矩形ABCD的边于点 F,若AB=4,AD=6,当点F为矩形ABCD边的中点时,AP的长为_____________.
类型四:图形性质探究
2021年中考数学总复习 拉分题训练课件 利润最值问题: 这是一份2021年中考数学总复习 拉分题训练课件 利润最值问题,共16页。
2021年中考数学总复习 拉分题训练课件 静态几何图形综合探究: 这是一份2021年中考数学总复习 拉分题训练课件 静态几何图形综合探究,共44页。PPT课件主要包含了等腰直角三角形等内容,欢迎下载使用。
2021年中考数学总复习 拉分题训练课件 函数图象问题: 这是一份2021年中考数学总复习 拉分题训练课件 函数图象问题,共31页。PPT课件主要包含了①②③④等内容,欢迎下载使用。












