数学人教版第五章 相交线与平行线综合与测试同步训练题

人教版2021年七年级下册第5章《相交线与平行线》达标测试卷

一．选择题（共10小题，满分30分，每小题3分）

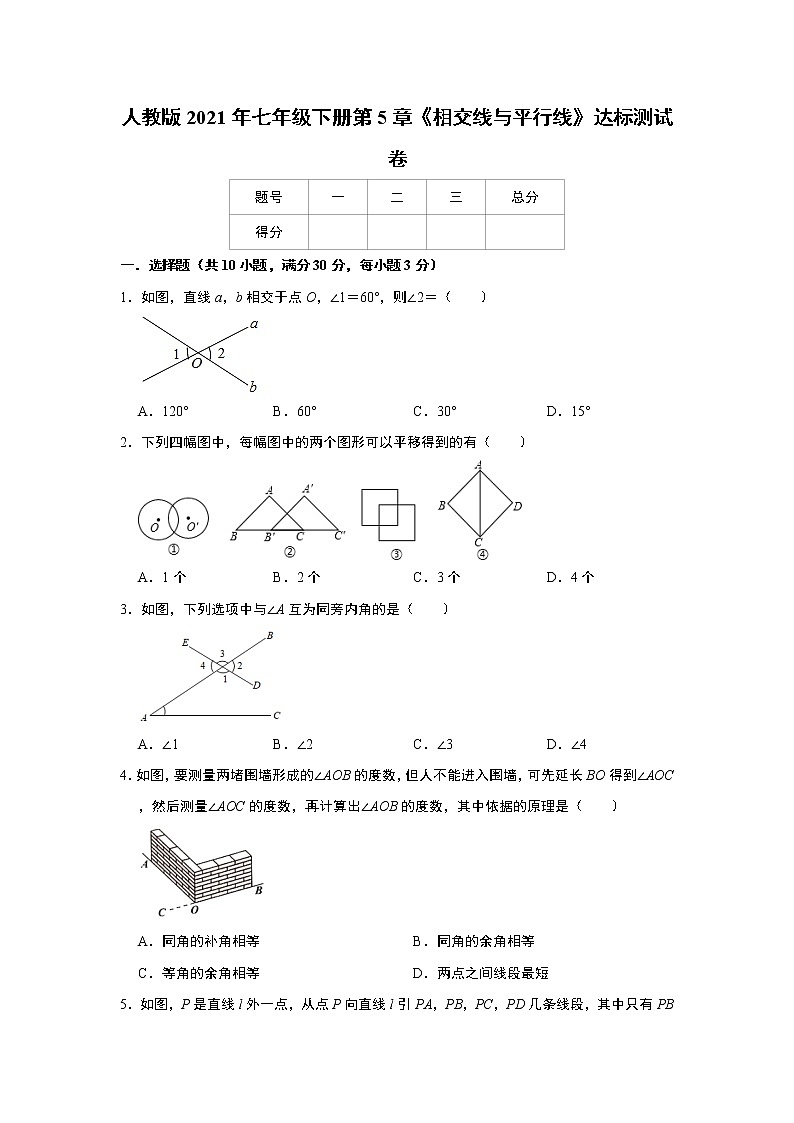
1．如图，直线a，b相交于点O，∠1＝60°，则∠2＝（　　）

A．120° B．60° C．30° D．15°

2．下列四幅图中，每幅图中的两个图形可以平移得到的有（　　）

A．1个 B．2个 C．3个 D．4个

3．如图，下列选项中与∠A互为同旁内角的是（　　）

A．∠1 B．∠2 C．∠3 D．∠4

4．如图，要测量两堵围墙形成的∠AOB的度数，但人不能进入围墙，可先延长BO得到∠AOC，然后测量∠AOC的度数，再计算出∠AOB的度数，其中依据的原理是（　　）

A．同角的补角相等 B．同角的余角相等 

C．等角的余角相等 D．两点之间线段最短

5．如图，P是直线l外一点，从点P向直线l引PA，PB，PC，PD几条线段，其中只有PB与l垂直，这几条线段中长度最短的是（　　）

A．PA B．PB C．PC D．PD

6．下列命题是真命题的是（　　）

A．如果两个角是内错角，那么它们一定相等 

B．如果两个角是同位角，那么它们一定相等 

C．如果两个角是同旁内角，那么它们一定互补 

D．如果两个角是对顶角，那么它们一定相等

7．如图，点O在直线AB上，CO⊥AB，若∠COD＝52°，则∠AOD的度数是（　　）

A．38° B．128° C．142° D．150°

8．如图，下列条件能判断AB∥CD的是（　　）

A．∠1＝∠3 B．∠2＝∠3 C．∠1＝∠4 D．∠2＝∠4

9．如图，若∠1＝35°，且AB∥CD，则∠2的度数是（　　）

A．125° B．135° C．145° D．155°

10．一把直尺和一块含30°角的直角三角板ABC如图所示摆放，直尺一边与三角板的两直角边分别交于点D和点E，另一边与三角板的两直角边分别交于点F和点A，且∠CED＝35°，那么∠BAF的大小为（　　）

A．5° B．15° C．25° D．35°

二．填空题（共8小题，满分32分，每小题4分）

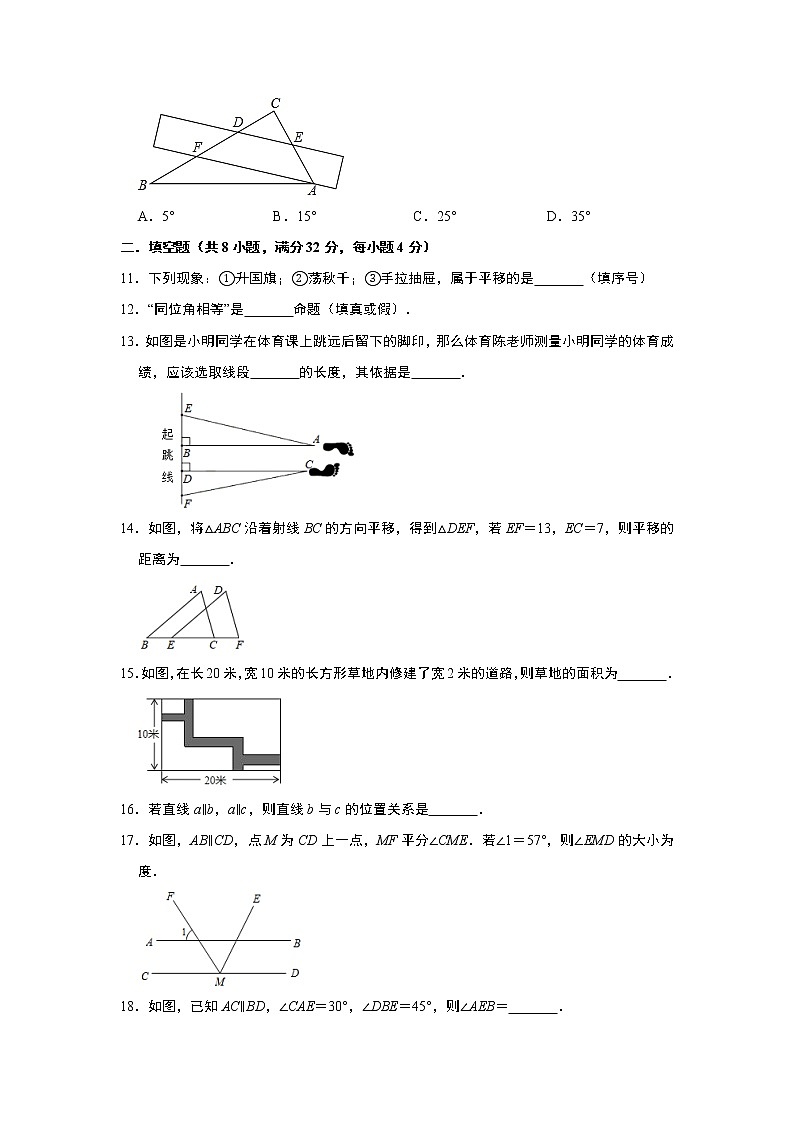
11．下列现象：①升国旗；②荡秋千；③手拉抽屉，属于平移的是　   　（填序号）

12．“同位角相等”是　   　命题（填真或假）．

13．如图是小明同学在体育课上跳远后留下的脚印，那么体育陈老师测量小明同学的体育成绩，应该选取线段　   　的长度，其依据是　   　．

14．如图，将△ABC沿着射线BC的方向平移，得到△DEF，若EF＝13，EC＝7，则平移的距离为　   　．

15．如图，在长20米，宽10米的长方形草地内修建了宽2米的道路，则草地的面积为　   　．

16．若直线a∥b，a∥c，则直线b与c的位置关系是　   　．

17．如图，AB∥CD，点M为CD上一点，MF平分∠CME．若∠1＝57°，则∠EMD的大小为　   　度．

18．如图，已知AC∥BD，∠CAE＝30°，∠DBE＝45°，则∠AEB＝　   　．

三．解答题（共7小题，满分58分）

19．（6分）如图，直线AB与直线MN相交，交点为O，OC⊥AB，OA平分∠MOD，若∠BON＝20°，求∠COD的度数．

20．（6分）如图，∠1＝∠2，∠3＝∠4，∠5＝∠6，求证：CE∥BF．

21．（7分）如图，在边长为1个单位长度的小正方形组成的网格中，△ABC的顶点A、B、C在小正方形的顶点上，将△ABC向右平移3单位，再向上平移2个单位得到三角形A1B1C1．

（1）在网格中画出三角形A1B1C1．

（2）A1B1与AB的位置关系　   　．

（3）三角形A1B1C1的面积为　   　．

22．（7分）如图，AD∥BC，∠1＝∠C，∠B＝60°，DE平分∠ADC交BC于点E，

试说明AB∥DE．请完善解答过程，并在括号内填写相应的理论依据．

解：∵AD∥BC，（已知）

∴∠1＝∠　   　＝60°．（　   　）

∵∠1＝∠C，（已知）

∴∠C＝∠B＝60°．（等量代换）

∵AD∥BC，（已知）

∴∠C+∠　   　＝180°．（　   　）

∴∠　   　＝180°﹣∠C＝180°﹣60°＝120°．（等式的性质）

∵DE平分∠ADC，（已知）

∴∠ADE＝∠ADC＝×120°＝60°．（　   　）

∴∠1＝∠ADE．（等量代换）

∴AB∥DE．（　   　）

23．（8分）如图，已知AB∥CD，E是直线AB上的一点，CE平分∠ACD，射线CF⊥CE，∠1＝32°，

（1）求∠ACE的度数；

（2）若∠2＝58°，求证：CF∥AG．

24．（12分）我们已经学过了对顶角、邻补角、同位角等，知道了它们的特征．现在若有两个角，它们不是同一个顶点，但这两角的两边相互平行，我们就把满足这个条件的两个角称作“平行角”．如图1，已知AB∥CD，AD∥BC，因此∠B和∠D是“平行角”．

（1）图1中，证明∠B＝∠D；

（2）如图2，延长DC到E，可知∠A和∠BCE也是“平行角”，但它们的数量关系是　   　；

（3）如图3，DE平分∠ADC，BF平分∠ABC，请说明图中的∠1和∠2是“平行角”．

25．（12分）如图，AE平分∠BAC，∠CAE＝∠CEA．

（1）如图1，求证：AB∥CD；

（2）如图2，点F为线段AC上一点，连接EF，求证：∠BAF+∠AFE+∠DEF＝360°；

（3）如图3，在（2）的条件下，在射线AB上取点G，连接EG，使得∠GEF＝∠C，当∠AEF＝35°，∠GED＝2∠GEF时，求∠C的度数．

参考答案

一．选择题（共10小题，满分30分，每小题3分）

1．解：如图，直线a，b相交于点O，∠1＝60°，则∠2＝60°．

答案：B．

2．解：①、②、③图形的形状和大小没有变化，符合平移的性质，属于平移得到；

④图形的方向发生变化，不符合平移的性质，不属于平移得到．

答案：C．

3．解：A、∠1和∠A是同旁内角，答案本选项符合题意；

B、∠2和∠A是同位角，不是同旁内角，答案本选项不符合题意；

C、∠3和∠A不是同旁内角，答案本选项不符合题意；

D、∠4和∠A是内错角，不是同旁内角，答案本选项不符合题意．

答案：A．

4．解：如图，由题意得，

∠AOC+∠AOB＝180°，

即∠AOC与∠AOB互补，

因此量出∠AOC的度数，即可求出∠AOC的补角，

根据同角的补角相等得出∠AOB的度数，

答案：A．

5．解：直线外一点P与直线l上各点连接的所有线段中，最短的是PB，依据是垂线段最短，

答案：B．

6．解：A、两直线平行，如果两个角是内错角，那么它们一定相等，原命题是假命题；

B、两直线平行，如果两个角是同位角，那么它们一定相等，原命题是假命题；

C、两直线平行，如果两个角是同旁内角，那么它们一定互补，原命题是假命题；

D、如果两个角是对顶角，那么它们一定相等，是真命题；

答案：D．

7．解：如图所示：∵CO⊥AB，

∴∠AOC＝90°，

∵∠COD＝52°，

∴∠AOD＝∠AOC+∠COD＝90°+52°＝142°．

答案：C．

8．解：A．根据∠1＝∠3不能证AB∥CD；

B．根据内错角相等，两直线平行即可证得AB∥CD；

C．根据内错角相等，两直线平行即可证得AD∥BC，不能证AB∥CD；

D．根据∠2＝∠4不能证AB∥CD．

答案：B．

9．解：记AB与EF的交点为点O，

∵AB∥CD，∠1＝35°，

∴∠EOB＝∠1＝35°，

∴∠2＝180°﹣∠EOB＝145°，

答案：C．

10．解：∵DE∥AF，∠CED＝35°，

∴∠CAF＝∠CED＝35°，

∵∠BAC＝60°，

∴∠BAF＝60°﹣35°＝25°．

答案：C．

二．填空题（共8小题，满分32分，每小题4分）

11．解：①升国旗是平移；②荡秋千，运动过程中改变了方向，不符合平移的性质；③手拉抽屉是平移；

答案答案为：①③．

12．解：同位角不一定相等，所以命题“同位角相等”是假命题．

答案答案为假．

13．解：小明同学的体育成绩，应该选取线段CD的长度．依据为：垂线段最短．

答案答案为：CD，垂线段最短．

14．解：∵△ABC沿着射线BC的方向平移，得到△DEF，

∴BE＝CF，

∵EF＝13，EC＝7，

∴BE+7+CF＝13，

即2BE+7＝13，解得BE＝3，

即平移的距离为3．

答案答案为3．

15．解：将道路分别向左、向上平移，得到草地为一个长方形，

长方形的长为20﹣2＝18（米），宽为10﹣2＝8（米），

则草地面积为18×8＝144米2．

答案答案为：144米2．

16．解：若直线a∥b，a∥c，则直线b与c的位置关系是平行，

答案答案为：平行．

17．解：∵AB∥CD，

∴∠CMF＝∠1＝57°，

∵MF平分∠CME，

∴∠CME＝2∠CMF＝114°．

又∵∠CME+∠EMD＝180°，

∴∠EMD＝180°﹣∠CME＝180°﹣114°＝66°．

答案答案为：66．

18．解：过点E作EF∥AC，

∵AC∥BD，

∴AC∥EF∥BD，

∴∠AEF＝∠CAE＝30°，∠BEF＝∠DBE＝45°，

∴∠AEB＝∠AEF+∠BEF＝75°．

答案答案为：75°．

三．解答题（共7小题，满分58分）

19．解：∵∠BON＝20°，

∴∠AOM＝20°，

∵OA平分∠MOD，

∴∠AOD＝∠MOA＝20°，

∵OC⊥AB，

∴∠AOC＝90°，

∴∠COD＝90°﹣20°＝70°．

20．证明：∵∠3＝∠4，

∴DF∥BC，

∴∠5＝∠BAF，

∵∠5＝∠6，

∴∠6＝∠BAF，

∴AB∥CD，

∴∠2＝∠AGE，

∵∠1＝∠2，

∴∠1＝∠AGE，

∴CE∥BF．

21．解：（1）如图所示，△A1B1C1即为所求．

（2）由平移的性质知A1B1∥AB，

答案答案为：平行；

（3）三角形A1B1C1的面积为×3×3＝，

答案答案为：．

22．解：∵AD∥BC，（已知）

∴∠1＝∠B＝60°．（ 两直线平行，同位角相等）

∵∠1＝∠C，（已知）

∴∠C＝∠B＝60°．（等量代换）

∵AD∥BC，（已知）

∴∠C+∠ADC＝180°．（两直线平行，同旁内角互补）

∴∠ADC＝180°﹣∠C＝180°﹣60°＝120°．（等式的性质）

∵DE平分∠ADC，（已知）

∴∠ADE＝∠ADC＝×120°＝60°．（角平分线定义）

∴∠1＝∠ADE．（等量代换）

∴AB∥DE．（内错角相等，两直线平行．）

答案答案为：B，两直线平行，同位角相等，ADC，两直线平行，同旁内角互补，ADC，角平分线定义，内错角相等，两直线平行．

23．解：（1）∵AB∥CD，

∴∠1＝∠DCE＝32°，

∵CE平分∠ACD，

∴∠ACE＝∠DCE＝32°；

（2）∵CF⊥CE，

∴∠FCE＝90°，

∴∠FCH＝90°﹣32°＝58°，

∵∠2＝58°，

∴∠FCH＝∠2，

∴CF∥AG．

24．解：（1）∵AB∥CD，

∴∠A+∠D＝180°，

∵AD∥BC，

∴∠A+∠B＝180°，

∴∠B＝∠D；

（2）由（1）得∠A+∠D＝180°，

∵AD∥BC，

∴∠D＝∠BCE，

∴∠A+∠BCE＝180°；

答案答案为：互补；

（3）∵AB∥CD，

∴EB∥DF，∠1＝∠AED，

∵DE平分∠ADC，BF平分∠ABC，

∴2∠1＝2∠2，

∴∠1＝∠2，

由（1）知∠ADC＝∠ABC，

∴∠2＝∠AED，

∴ED∥BF，

∴∠1和∠2是“平行角”．

25．（1）证明：∵AE平分∠BAC，

∴∠BAE＝∠CAE，

∵∠CAE＝∠CEA，

∴∠CEA＝∠BAE，

∴AB∥CD；

（2）证明：过F作FM∥AB，如图，

∵AB∥CD，

∴AB∥FM∥CD，

∴∠BAF+∠AFE＝180°，∠DEF+∠EFM＝180°，

∴∠BAF+∠AFM+∠DEF+∠EFM＝360°，

即∠BAF+∠AFE+∠DEF＝360°；

（3）解：设∠GEF＝∠C＝x°，

∵∠GEF＝∠C，∠GED＝2∠GEF，

∴∠GED＝2x°，

∵AB∥CD，

∴∠C+∠BAC＝180°，

∴∠BAC＝180°﹣x°，

∵AE平分∠BAC，

∴∠BAE＝BAC＝（180°﹣x°）＝90°﹣x°，

由（1）知：AB∥CD，

∴∠BAE+∠AED＝180°，

∵∠AEF＝35°，

∴90﹣x+x﹣35+2x＝180，

解得：x＝50，

即∠C＝50°．