人教版八年级下册18.1.2 平行四边形的判定图文ppt课件

这是一份人教版八年级下册18.1.2 平行四边形的判定图文ppt课件，共32页。PPT课件主要包含了教学目标，重点难点，导入新课，平行四边形的判定，想一想，新知详解，逆命题成立，在四边形ABCD中，同理可证ABDC，ADCB等内容，欢迎下载使用。

1.平行四边形的判定方法。 2.能根据判别方法进行有关的应用。
重点：探索并证明平行四边形的判定方法。难点：正确并灵活运用几种判定方法解决问题。
平行四边形的两组对边分别相等；
平行四边形的两组对角分别相等；
平行四边形的对角线互相平分。
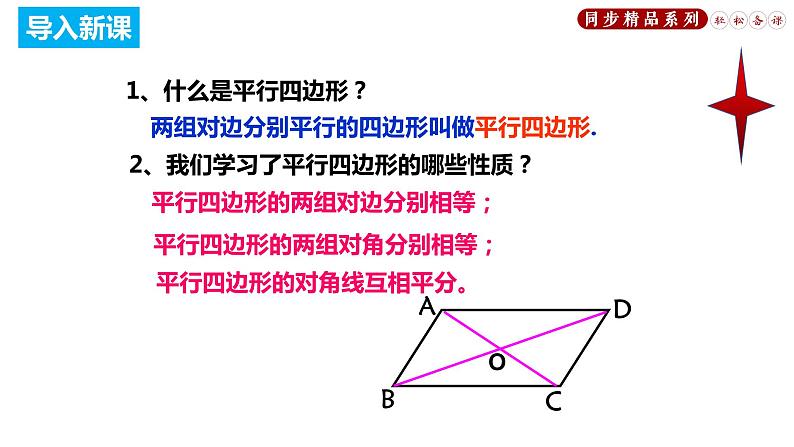
两组对边分别平行的四边形叫做平行四边形.
2、我们学习了平行四边形的哪些性质？
1、什么是平行四边形？
1、平行四边形的对边相等；
2、平行四边形的对角相等；
3、平行四边形的对角线互相平分。
你能说出平行四边形三条性质的逆命题吗？
逆命题：两组对角分别相等的四边形是平行四边形；
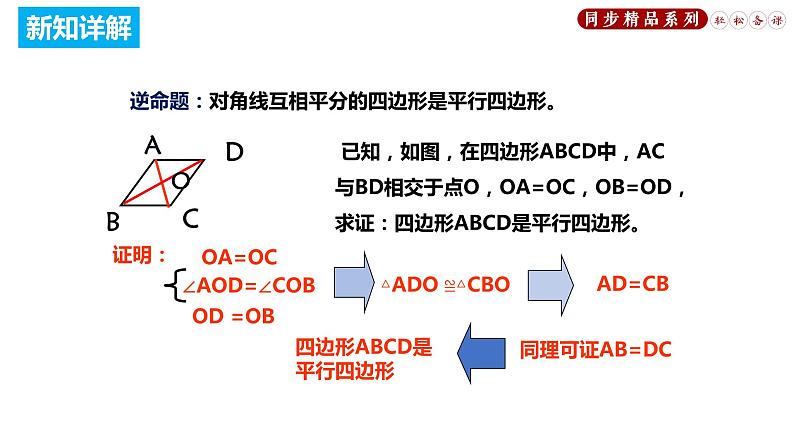
逆命题：对角线互相平分的四边形是平行四边形。
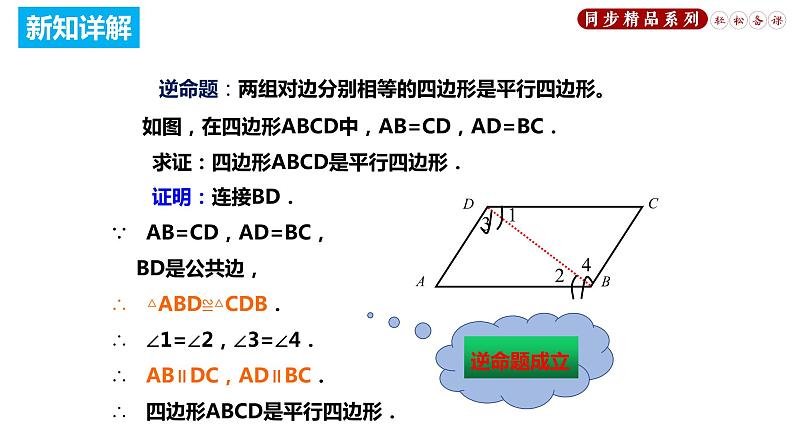
逆命题：两组对边分别相等的四边形是平行四边形；
　　证明：连接BD．∵　AB=CD，AD=BC， BD是公共边，∴　△ABD≌△CDB．∴　∠1=∠2，∠3=∠4．∴　AB∥DC，AD∥BC．∴　四边形ABCD是平行四边形．
　　如图，在四边形ABCD中，AB=CD，AD=BC．　　求证：四边形ABCD是平行四边形．
　　 　逆命题：两组对边分别相等的四边形是平行四边形。　　
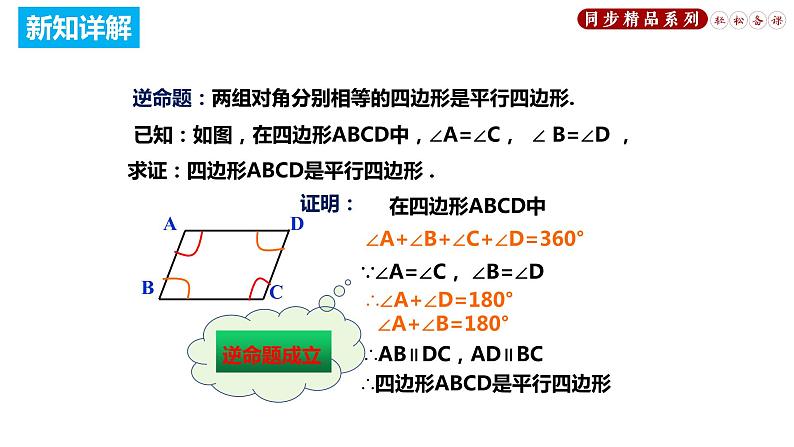
逆命题：两组对角分别相等的四边形是平行四边形.
∴AB∥DC，AD∥BC
∠A+∠B+∠C+∠D=360°
已知：如图，在四边形ABCD中，∠A=∠C， ∠ B=∠D ，求证：四边形ABCD是平行四边形 .
∴四边形ABCD是平行四边形
∵∠A=∠C， ∠B=∠D
∴∠A+∠D=180° ∠A+∠B=180°
已知，如图，在四边形ABCD中，AC与BD相交于点O，OA=OC，OB=OD，求证：四边形ABCD是平行四边形。
△ADO ≌△CBO
四边形ABCD是平行四边形
平行四边形的判定定理1：
两组对角分别相等的四边形是平行四边形。
对角线互相平分的四边形是平行四边形。
两组对边分别相等的四边形是平行四边形。
平行四边形的判定定理2：
平行四边形的判定定理3：
例3.如图，□ABCD中，E，F分别是对角线AC 上的两点，并且AE=CF．求证：四边形BFDE是平行四边形．
∵四边形ABCD是平行四边形，
∴OA=OC， OB=OD.
∴四边形BFDE是平行四边形.
∴OA-AE=OC-CF，
证明：∵ABCD是平行四边形， O是对角线AC、BD交点 ∴AD=BC,∠DAE=∠BCF 又∵AE=CF ∴△DAE≌△BCF ∴DE=BF 同理△BAE≌△DCF ∴BE=DF ∴四边形BFDE是平行四边形
你还能用其他方法证明吗？
1.在下列条件中，不能确定四边形ABCD为平行四边形的是（　　）A．∠A=∠C，∠B=∠DB．∠A=∠B=∠C=90°C．∠A+∠B=180°，∠B+∠C=180°D．∠A+∠B=180°，∠C+∠D=180°
分析：（A）∠A=∠C，∠B=∠D，根据四边形的内角和为360°，可推出∠A+∠B=180°，所以AD∥BC，同理可得AB∥CD，所以四边形ABCD为平行四边形，故A选项正确；（B）∠A=∠B=∠C=90°，则∠D=90°，四个内角均为90°可以证明四边形ABCD为矩形，故B选项正确；（C）∠A+∠B=180°，∠B+∠C=180°即可证明AB∥CD，AD∥BC，根据平行四边形的定义可以证明四边形ABCD为平行四边形，故C选项正确；（D）∠A+∠B=180°，∠C+∠D=180°即可证明AD∥BC，条件不足，不足以证明四边形ABCD为平行四边形，故D选项错误．故选 D．
2. 点A是直线l外一点，在l上取两点B、C，分别以A、C为圆心，BC、AB长为半径画弧，两弧交于点D，分别连接AB、AD、CD，则四边形ABCD一定是（　　）A．平行四边形B．矩形C．菱形D．梯形
分析：∵分别以A、C为圆心，BC、AB长为半径画弧，两弧交于点D，∴AD=BC AB=CD∴四边形ABCD是平行四边形（两组对边分别相等的四边形是平行四边形）。故选A。
3.小明动手操作如下，先剪一个等腰三角形纸片ABC，使AB=AC，再把∠B沿EM折叠，使点B落在点D上；把∠C沿FN折叠，使点C落在点D上，则四边形AEDF是平行四边形，你认为正确吗？请说明理由.
解析：四边形AEDF是平行四边形；理由如下： ∵AB=AC， ∴∠B=∠C， 根据折叠的性质，∠B=∠BDE，∠C=∠CDF ∴∠B=∠CDF，∠C=∠BDE， ∴DF∥AB，DE∥AC， ∴四边形AEDF是平行四边形。
思考：如果只考虑一组对边，它们满足什么条件时能成为平行四边形呢？
平行四边形中， AB∥DC且AB=DC。
猜想：一组对边平行且相等的四边形是平行四边形。
如图，在四边形ABCD中，AB//CD，AB=CD，求证：四边形ABCD是平行四边形.
∵AB //CD ，∴∠1=∠2．又∵AB =CD ， AC =CA ，∴△ABC≌△CDA．∴BC =DA ．∴四边形ABCD是平行四边形．
平行四边形的判定定理4：
一组对边平行且相等的四边形是平行四边形。
∵ AB∥DC且AB=DC，∴四边形ABCD为平行四边形。
想一想：一组对边平行，另一组对边相等的四边形是平行四边形吗？
一组对边平行，另一组对边相等的四边形是平行四边形或等腰梯形.
例4：如图，在□ABCD中，E，F分别是AB，CD的中点．求证：四边形EBFD是平行四边形 。
∴AB=CD，EB∥FD.
∴四边形EBFD是平行四边形.
∵E，F分别是AB，CD的中点
4.在四边形ABCD，从下列条件中任取两个组合，使得四边形ABCD是平行四边形的组合有（　　）种． ①AB∥CD；‚②BC∥AD；③ƒAB=CD；④BC=AD．A．2组B．3组C．4组D．6组
分析：根据平行四边形的判定方法，符合条件的有4种，分别是：①②、③④、①③、②④．故选：C．
5.如图，在△ABC中，D是BC上的点，O是AD的中点，过A作BC的平行线交BO的延长线于点E，则四边形ABDE是什么四边形？并说明理由
分析：根据平行线性质求出∠EAO=∠ODB，∠AEO=∠DBO，证△AOE≌△DOB，推出OB=OE，根据平行四边形的判定求出即可
解析：四边形ABDE是平行四边形，理由是：∵AE∥BC，∴∠EAO=∠ODB，∠AEO=∠DBO，∵O是AD的中点，∴AO=OD，∵在△AOE和△DOB中∵∠EAO＝∠BDO；∠AEO＝∠DBO；AO＝OD，∴△AOE≌△DOB，∴OB=OE，∵AO=OD，∴四边形ABDE是平行四边形。
6.如图，E、F是△ABC的边AB、BC边的中点，在AC上取G、H两点，使AG=GH=HC，连接EG、FH并延长交于点D求证：四边形ABCD是平行四边形
分析：连接BD交AC于O，连结BG，BH，首先证得四边形BHDG是平行四边形得到AO=OC，然后利用对角线互相平分的四边形是平行四边形判定即可．
解析：连接BD交AC于O，连结BG，BH，∵E是AB中点，AG=GH，∴EG是△ABH的一条中位线，∴EG∥BH，即GD∥BH，同理可证BG∥DH，∴四边形BHDG是平行四边形．∴BO=OD，GO=OH，又∵AG=HC，∴AG+GO=HC+OH，即AO=OC，又∵BO=OD，∴四边形ABCD是平行四边形
平行四边形的判定方法共有几种？
1.在平面直角坐标系中，有A（0，1），B（-1，0），C（1，0）三点，若点D与A，B，C三点构成平行四边形，则点D的坐标不可能是（　　）A．（0，-1）B．（-2，1）C．（-2，-1）D．（2，1）
分析：如图所示∵两组对边分别平行的四边形是平行四边形∴可以分以下三种情况分别求出D点的坐标：如图所示：①当AB∥CD，AD∥BC时，D点的坐标为（2，1）；②当AB∥CD，AC∥BD时，D点的坐标为（0，-1）；③当AD∥BC，AC∥BD时，D点的坐标为（-2，1）．故选：C．
2.梯形ABCD中AD∥BC且AB=DC，AD=10cm，BC=6cm,P、Q分别从A、C同时出发，P以2cm/s的速度由A向D运动，Q以4cm/s的速度由C出发向B运动，问：（1）求出几秒后四边形ABQP是平行四边形？（2）若P仍以2cm/s的速度由A向D运动，而Q点到达点B后立即返回以4cm/s的速度向点C运动，求出点Q从点C出发经过几秒后四边形ABQP第二次构成平行四边形？
证明：（1）设t秒后四边形ABQP是平行四边形；根据题意得：AP=2tcm，CQ=4tcm，则BQ=（6-4t）cm；∵AD∥BC，∴当AP=BQ时，四边形ABQP是平行四边形，∴2t=6-4t，解得：t=1，即1秒后四边形ABQP是平行四边形；