初中数学人教版七年级下册5.1.1 相交线教课内容课件ppt

这是一份初中数学人教版七年级下册5.1.1 相交线教课内容课件ppt，共33页。

【高效课堂】人教（新课标版）七年级数学下册
第五章 《相交线与平行线》核心考点梳理
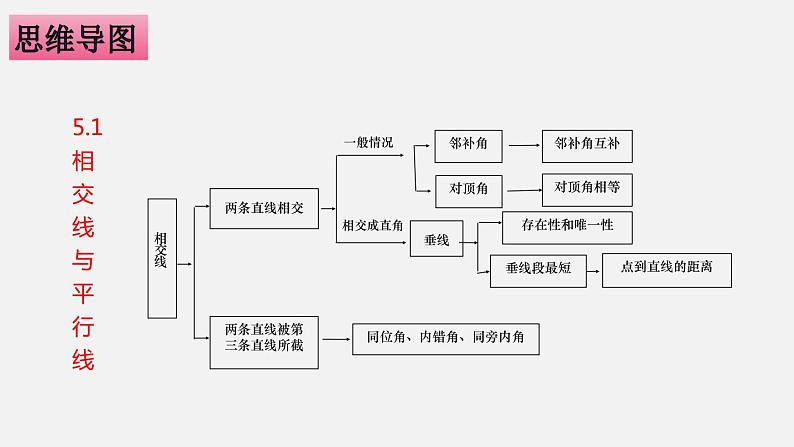
5.1 相交线与平行线
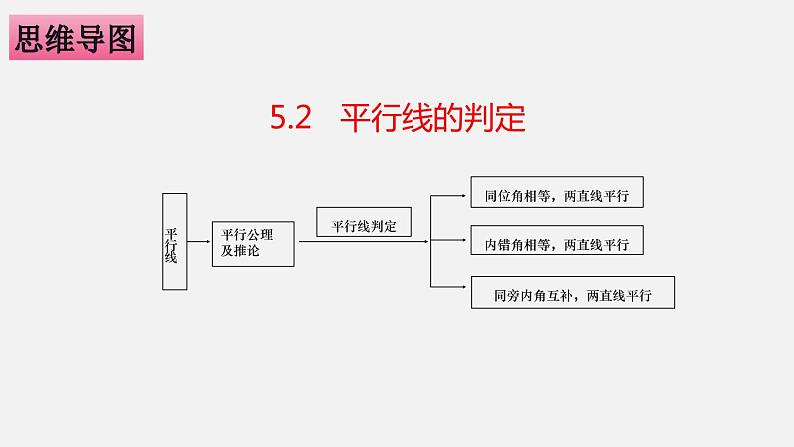
5.2 平行线的判定
5.3 平行线的性质
两条直线的位置关系有相交、平行。
角的两边互为反向延长线
4、如图，直线AB，CD被直线EF所截，那么图中对顶角有（ ）
A.5对 B.4对C.3对 D.2对
5、三条直线相交于同一点时，对顶角有m对，交于不同三点时，对顶角有n对，则m与n的关系是（ ）
当两条直线相交时，有2对对顶角，4对邻补角。
A、m=n B、m>n C、m数对顶角、邻补角的个数
ｎ条直线相交于一点，有　 　　　对对顶角。
1、互为对顶角的两个角的平分线（ ）A、重合 B、互为反向延长线C、互相垂直 D、不能确定
2、互为邻补角的两个角的平分线（ ）A、重合 B、互为反向延长线C、互相垂直 D、不能确定
对顶角相等 邻补角互补
1.垂直的定义: 两条直线相交，所构成的四个角中，有一个角是90°时，就说这两条直线互相垂直。其中一条直线叫做另一条直线的垂线。它们的交点叫垂足。
2. 垂线的性质: (1)过一点有且只有一条直线与已知直线垂直。(2): 直线外一点与直线上各点连结的所有线段中，垂线段最短。简称:垂线段最短。
3.点到直线的距离: 从直线外一点到这条直线的垂线段的长度，叫做点到直线的距离。
4.如遇到线段与线段，线段与射线，射线与射线，线段或射线与直线垂直时，特指它们所在的直线互相垂直。
5.垂线是直线，垂线段特指一条线段是图形，点到直线距离是指垂线段的长度，是指一个数量，是有单位的。
1、 两条直线相交所成的四个角中，下列条件中能判定两条直线垂直的是 （A） 有两个角相等 （ B）有两对角相等 （C） 有三个角相等 （ D）有四对邻补角
垂直的定义：当两条直线相交所成的四个角中，有一个角是直角时，这两条直线互相垂直，其中一条直线叫另一条直线的垂线，它们的交点叫垂足。
注意:画线段(或射线)的垂线时,有时要将线段延长(或将射线反向延长)后再画垂线。
2、画一条已知线段的垂线，垂足一定在（ ） A、线段上 B、线段的端点 C、线段的延长线上 D、线段所在的直线上
3、下列说法中，正确的是（ ）A、一条直线有且只有一条垂线B、过一点不一定能向一条射线或线段所在的直线作垂线C、若a⊥b，b⊥c，则一定有a⊥cD、过一点只能向已知直线作一条垂线
结论: 过一点有且只有一条直线与已知直线垂直
5、已知A、B两点之间距离是3，l 是经过点B的一条直线，则点A到直线 l 的距离是（ ）A、h﹥3 B、h=3 C、h﹤3 D、h≦3
4、下列说法正确的是（ ）
直线外一点到这条直线的垂线段的长度，叫做点到直线的距离。连接直线外一点与直线上各点的所有线段中，垂线段最短。
当两条直线被第三条直线所截时
1、如图，下列各对角分别是哪两条直线被哪条直线所截形成的？它们各是什么角？（1）∠1和∠2；（2）∠1和∠3；（3）∠1和∠4；（4）∠3和∠4
归纳：对于两个角是由哪两条直线被第三条直线所截的问题中，
就先观察组成这两个角的边中，公共的边是哪一条，这一条就是截线，而另两条非公共的直线就是被截的直线。
2、如图，图中共有 对同旁内角
一个三角形内有3对同旁内角；一个四边形内有4对同旁内角。
数同位角、内错角、同旁内角的对数
平行线的概念:在同一平面内,不相交的两条直线叫做平行线。
2. 两直线的位置关系: 在同一平面内，两直线的位置关系只有两种:(1)相交; (2)平行。
3. 平行线的基本性质:
(1) 平行公理(平行线的存在性和唯一性) 经过直线外一点，有且只有一条直线与已知直线平行。
(2) 推论(平行线的传递性) 如果两条直线都和第三条直线平行，那么这两条直线也互相平行。
4.同位角、内错角、同旁内角的概念
同位角、内错角、同旁内角，指的是一条直线分别与两条直线相交构成的八个角中，不共顶点的角之间的特殊位置关系。它们与对顶角、邻补角一样，总是成对存在着的。
1、同位角的位置特征是:
2、内错角的位置特征是:
3、同旁内角的位置特征是:
(1)在被截两直线的同方，
(1)在被截两直线之间，
(2)在截线的同一旁。
（1）不相交的两条直线叫做平行线。（ ）
（2）有且只有一个公共点的两条直线是相交直线（ ）
（4）在同一平面内不相交的两条线段必平行。 （ ）
（3）没有公共点的两条直线是平行线。( )
（5）同一平面内的两条直线，必把这个平面分成四部分。 （ ）
2、下列说法正确的是（ ）A、在同一平面内，两条直线的位置关系有相交、 垂直、平行三种B、在同一平面内，不垂直的两直线必平行C、在同一平面内，不平行的两直线必垂直D、在同一平面内，不相交的两直线一定不垂直
注意：1、在平行线的定义中，一定要注意 “在同一平面内”这一前提条件。2、垂直是相交的一种特殊情形。
3、同一平面内互不重合的三条直线公共点的个数可能是（ ）（A）1个或3个 （B）2个或3个（C）1个或2个或3个 （D）0个或1个或2个或3个
4、下列说法中，哪个正确？（ ）A、过一点有且只有一条直线与已知直线平行B、过一点有且只有一条直线与已知直线垂直C、两条不相交的直线是平行线D、若线段AB与CD没有交点，则AB∥CD
两条直线平行的判定方法:
方法1：同位角相等，两直线平行。
方法2：内错角相等，两直线平行。
方法3：同旁内角互补，两直线平行。
方法4：如果两条直线都和第三条直线平行， 那么这两条直线也互相平行。
方法6：平行线的定义。
方法5：在同一平面内，如果两条直线都垂直于 同一条直线，那么这两条直线平行。 （垂直于同一直线的两直线平行）
练习:如果∠A和∠B是同位角，∠A=60。，则∠B的度数 （ ）A.60。 B. 120。 C. 60。或 120。 D.不能确定
注意：同位角不一定相等。同位角相等是平行线特有的性质，只有当两直线平行时，才有同位角相等。
考考你：图中如果AC∥BD 、AE ∥BF ，那么 ∠A与∠B的关系如何？你是怎样思考的？
AC∥BD， AE ∥BF
一个角的两边与另一个角的两边分别平行,则这两个角相等。
考考你：图中如果a∥b，那么∠1与∠2的角平分线的关系如何？你是怎样思考的？
∠2与∠3的角平分线呢？
∠2与∠4的角平分线呢？
两条直线平行，那么它们的同位角的角平分线也互相平行；内错角的角平分线也互相平行；同旁内角的角平分线互相垂直。
1、如图，已知AC⊥AE，BD⊥BF，∠1=35°，∠2=35°，AC与BD平行吗？AE与BF平行吗？为什么？
2、如图，已知∠A＝∠1，∠C＝∠D，试说明FD∥BC。
3、(2002.河南)如图所示，已知AB∥CD，直线EF分别交AB，CD于点E，点F，EG平分∠BEF，若∠1=72°，则∠2=_______。
，∠1=∠2，求证∠3=∠4。
5、如图，M、N、T和P、Q、R分别在同一直线上，且∠1=∠3，∠P=∠T，求证：∠M=∠R。
6、如图2，AC∥BE，AD平分∠BAC，∠1=∠ADC，AB∥CD吗？请说明理由。
解：∵AC∥BE, ∴ ∠1=∠4,(两直线平行，内错角相等） ∵ AD平分∠BAC, ∴ ∠3=∠4(角平分线性质) ∴ ∠1= ∠3(等量代换) 又∵ ∠1=∠2, ∴ ∠2=∠3,∴ AB∥CD(内错角相等,两直线平行)
7.如图1，MA1∥NA2，则∠A1＋∠A2＝_________________度。 如图2，MA1∥NA3，则∠A1＋∠A2＋∠A3＝_____________度。如图3，MA1∥NA4，则∠A1＋∠A2＋∠A3＋∠A4＝________度。如图4，MA1∥NA5，则∠A1＋∠A2＋∠A3＋∠A4＋∠A5＝__度。从上述结论中你发现了什么规律？
如图5，MA1∥NAn，则∠A1＋∠A2＋∠A3＋……＋∠An＝_________________度。
1. 命题的概念: 判断一件事情的句子，叫做命题。命题必须是一个完整的句子; 这个句子必须对某件事情做出肯定或者否定的判断。两者缺一不可。
2. 命题的组成: 每个命题是由题设、结论两部分组成。题设是已知事项；结论是由已知事项推出的事项。 命题常写成“如果……，那么……”的形式。或 “若……，则……”等形式。真命题和假命题：命题是一个判断，这个判断可能是正确的，也可以是错误的。由此可以把命题分成真命题和假命题。真命题就是: 如果题设成立，那么结论一定成立的命题。假命题就是: 如果题设成立时，不能保证结论总是成立的命题。
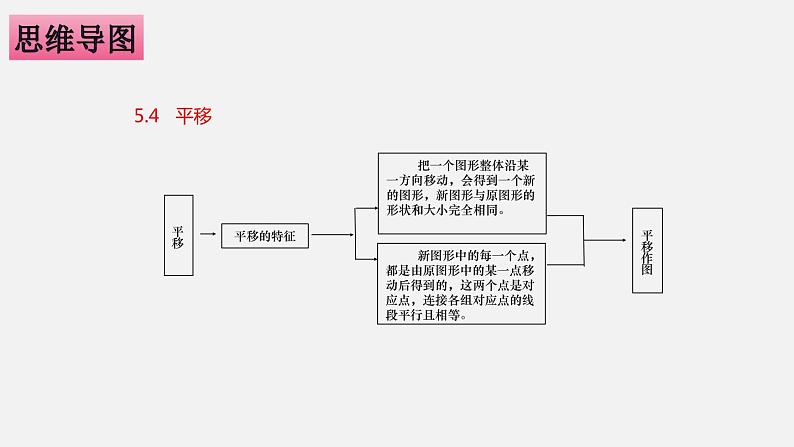
站在运动着的电梯上的人左右推动的推拉窗扇小李荡秋千运动躺在火车上睡觉的旅客
例1. 在以下生活现象中，不是平移现象的是（ ）