初中数学沪科版八年级下册20.2 数据的集中趋势与离散程度一等奖课件ppt

这是一份初中数学沪科版八年级下册20.2 数据的集中趋势与离散程度一等奖课件ppt，共30页。PPT课件主要包含了一组数据中，叫做这组数据的众数，出现次数最多的数据，SA2＝，SB2＝，S甲2＝，S乙2＝，a2s2，变式练习，本节课你有什么收获等内容，欢迎下载使用。

（x1+x2+x3+···+xn）
x1，x2，x3，···，xn表示各个数据.
其中n表示数据的总个数，
② 当一组数据大部分都在某一常数a附近上下波动时，
（ ）
其中a表示各个数据中较“整”的数，
分别表示各个数据与a的差,
3、加权平均数计算方法：
这n个数据的加权平均数.
在总结果中的比重，
一般地，对上面的加权平均数，可统一用下面的公式：
我们称其为各数据的权，
其中f1，f2，f3，…，fk
x1，x2，x3，…，xk
表示数据x1，x2，x3，…，xk
位于正中间的一个数据
(当数据的个数是偶数时)，
当将一组数据按大小顺序排列后，
(当数据的个数是奇数时)
正中间两个数据的平均数
叫做这组数据的中位数.
n 为奇数时，中间位置是第 个n为偶数时，中间位置是第 , 个
你知道中间位置如何确定吗?
若x1，x2，x3，···，xn的平均数为 ，则：
(1) nx1，nx2，nx3，···，nxn的平均数为 .
(2) x1+b，x2+b，x3+b，···，xn+b的平均数为 .
(3) nx1+b，nx2+b，nx3+b，···，nxn+b的平均数为 .
拓展练习： 若x1,x2,…, xn 的平均数为 ，y1,y2,…, yn 的平均数为 ，则 x1+y1，x2+y2，x3+y3，···，xn+yn 的平均数为 .
从数据集中趋势这个角度
（ ）
（ ）
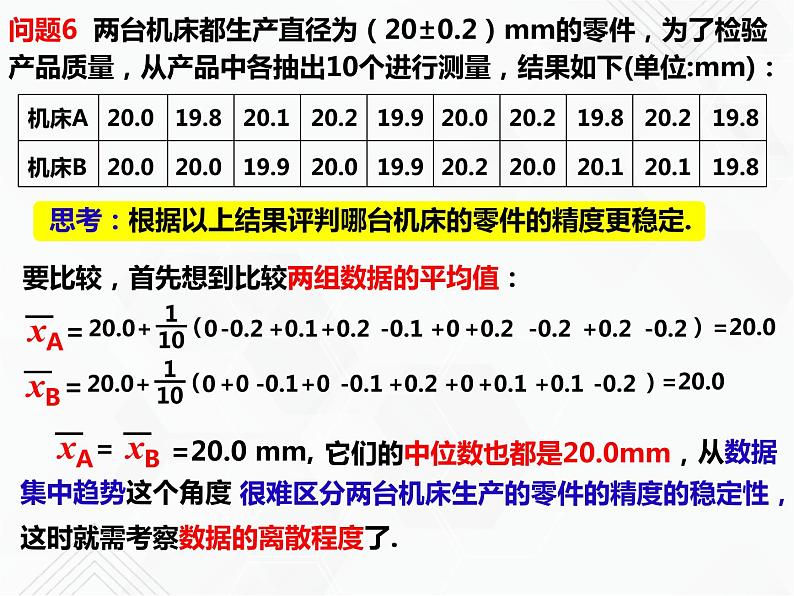
问题6 两台机床都生产直径为（20±0.2）mm的零件，为了检验产品质量，从产品中各抽出10个进行测量，结果如下(单位:mm)：
思考：根据以上结果评判哪台机床的零件的精度更稳定.
要比较，首先想到比较两组数据的平均值：
这时就需考察数据的离散程度了.
它们的中位数也都是20.0mm，
很难区分两台机床生产的零件的精度的稳定性，
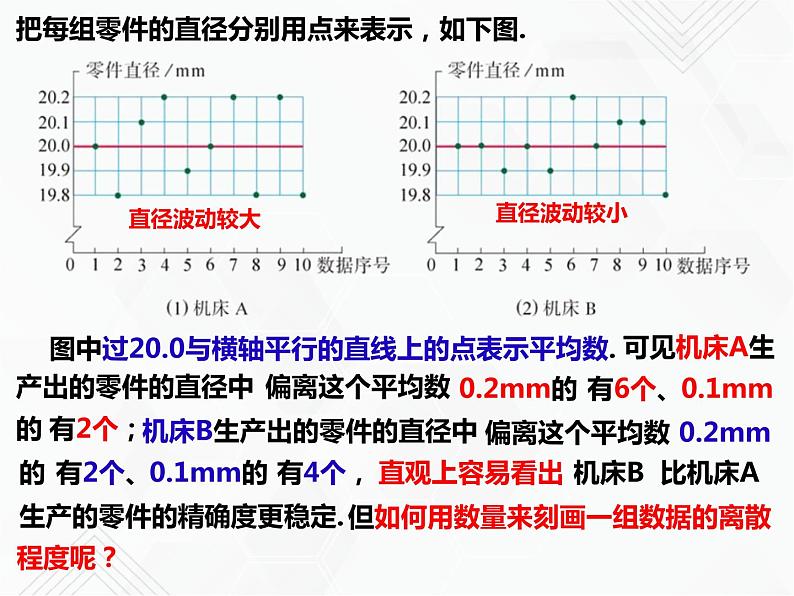
但如何用数量来刻画一组数据的离散程度呢？
可见机床A生产出的零件的直径中
把每组零件的直径分别用点来表示，如下图.
图中过20.0与横轴平行的直线上的点表示平均数.
机床B生产出的零件的直径中
生产的零件的精确度更稳定.
才利用方差来判断它们的波动情况．
统计学中常用下面的方法：
x1，x2，···，xn，
它们的平均数是 ，
[ ]
( x1 - )2
+( x2 - )2
+( xn - )2
来衡量这组数据的离散程度，
反映的是数据在平均数附近波动的情况.
方差是用来衡量一组数据波动大小的重要量，
当两组数据的平均数相等或相近时，
比机床B生产的10个零件直径
下面通过计算方差，
前面已经算得A,B两组数的平均数，于是
[ ]
+(19.8-20)2
[ ]
[ ]
由于0.026＞0.012，
可知机床A生产的10个零件直径
方差的单位是所给数据单位的平方.
必须认清公式中每个字母代表的意义，
x1，x2，···，xn 表示
对应练习

[( x1 - 10)2
+( x2 - 10 )2
+( x3 - 10 )2
+( x4 - 10 )2
+( x5 - 10 )2]
中，数5，10分别表示这个样本的（ ）.
A.容量，平均数 B.平均数，中位数C.众数，中位数 D.中位数，容量
利用方差的公式求方差时，
思考：计算一组数据的方差的一般步骤.
计算这组数据的方差s2
2、求下列两组数据的方差，并说明哪组数据的离散程度较小.
A：30，50，50，50，60 B：30，44，50，56，60
(30+50+50+50+60)＝
(30+44+50+56+60)＝
∴ A组数据的离散程度小
我们也常有样本方差估计
例6 为了比较甲、乙两个新品种水稻产品质量，收割时抽取了五块具有相同条件的试验田地，分别称得它们的质量，得其每公顷产量如下表（单位：1）：
(1) 哪个品种平均每公顷的产量较高？(2) 哪个品种的产量较稳定？
与用样本平均数估计总体平均数一样，
解：甲、乙两个新品种在试验田中的产量各组成一个样本.
下面我们来考察甲、乙两个新品种的稳定性.
（12.6+12+12.3+11.7+12.9）
（12.3+12.3+12.3+11.4+13.2）
说明甲、乙两个新品种平均每公顷的产量一样高.
(12.6-12.3)2
+(12-12.3)2
+(12.3-12.3)2
+(11.7-12.3)2
+(12.9-12.3)2
(12.3-12.3)2
+(11.4-12.3)2
+(13.2-12.3)2
则意味着这组数据对平均数的离散程度也越大.
乙品种每公顷的产量波动要小，
可知，甲品种每公顷的产量波动
② 在两组数据的平均数相差较大时，
由此估计甲品种的稳定性好.
① 一般地，在平均数相同的情况下，
以及在比较单位不同的两组数据时，
不能直接用方差来比较它们的离散程度.
再利用样本方差来估计总体数据的波动情况．
(1) 在解决实际问题时，方差的作用是什么？
可用样本方差估计总体方差．
(2) 运用方差解决实际问题的一般步骤是怎样的？
先计算样本数据平均数，
1、在一次射击训练中，甲、乙两人各射击10次，两人10次射击成绩的平均成绩是9.1环，方差分别是s甲2=1.2，s乙2=1.6，则关于甲、乙两人在这次射击训练中成绩稳定性的描述正确的是( ).
A. 甲比乙稳定 B.乙比甲稳定 C.甲和乙一样稳定 D.甲和乙的稳定性没法比较
2、一组数据6，4，a，3，2 的平均数是5，这组数据的方差为( ).
A. 8 B.5 C.4 D.3
3、数据0，-1，6，1，x 的众数为-1，则这组数据的方差为（ ）.
A. B. C. D.
4、已知一组数据 -3，-2，1，3，6，x 的中位数为1，则其方差为( ).
A. 8 B.9 C.10 D.11
① 新数据x1+b，x2+b，···，xn+b的方差为 .
② 新数据ax1，ax2，···，axn的方差为 .
③ 新数据ax1+b，ax2+b，···，axn+b的方差为 .
请你用发现的结论来解决以下的问题：已知数据a1，a2，a3，…，an的平均数为X，方差为Y, 则 ① 数据a1+3，a2 + 3，a3 +3 ，…，an +3的平均数为 ，方差为 . ② 数据a1-3，a2 -3，a3 -3 ，…，an -3的平均数为 ，方差为 . ③ 数据3a1，3a2 ，3a3 ，…，3an的平均数为 ，方差为 . ④数据2a1-3，2a2 -3，2a3 -3 ，…，2an -3的平均数为 ，方差为 .
1、已知数据x1、x2、x3、x4、x5的方差是 3， 那么数据 x1－1，x2－1，x3－1，x4－1，x5－1的方差是（ ） A.1 B.2 C.3 D.4
2、（探究题）已知数据x1、x2、x3、x4、x5的平均数是2，方差是 ，那么另一组数据2x1－1，2x1－1,2x1－1，2x1－1，2x1－1的平均数和方差分别是（ ） A、2， B、4， C、2， D、3，
2、考察甲、乙两种小麦的长势，分别从中抽取10株苗，测得苗高如下(单位：cm)： 甲：12，13，14，15，10，16，13，11，15，11； 乙：11，16，17，14，13，19，6，8，10，16.计算甲、乙两组数据的方差，说明哪种小麦长得较整齐.
(12+13+14+15+10+16+13+11+15+11)
(11+16+17+14+13+19+6+8+10+16)
[(12－13)2+(13－13)2 +(14－13)2 +(15－13)2 +(10－13)2+(16－13)2+(13－13)2+(11－13)2 +(15－13)2+(11－13)2]
∴ 甲种小麦长得比较整齐.
[(11－13)2+(16－13)2 +(17－13)2 +(14－13)2 +(13－13)2+(19－13)2+(6－13)2+(8－13)2 +(10－13)2+(16－13)2]
S2＝ [(0.25－0.152)2+(0.16－0.152)2 +(0.16－0.152)2 +(0.15－0.152)2+(0.20－0.152)2+(0.13－0.152)2+(0.10－0.152)2+(0.18－0.152)2+(0.14－0.152)2+(0.12－0.152)2 +(0.13－0.152)2+(0.13－0.152)2+(0.18－0.152)2+(0.15－0.152)2+(0.10－0.152)2]
3、在对某玉米品种进行考察时，农科所从一块试验田里随机抽取了15 株玉米，称得各株玉米的产量如下(单位：kg)：　　　0. 25，0. 16，0. 16，0. 15，0. 20，0. 13，0. 10，0. 18，0. 14，0. 12，0. 13，0. 13，0. 18，0. 15，0. 10.由此估计这块试验田每株玉米产量的方差是多少？
解：产量的平均数为：(0. 25+0. 16+0. 16+0. 15+0. 20+0. 13+0. 10+0. 18+0. 14+0. 12+0. 13+0. 13+0. 18+0. 15+0. 10)÷15
答：这块试验田每株玉米产量的方差是0.0014.
2、计算一组数据的方差的一般步骤.
3、在实际问题中，与用样本平均数估计总体平均数一样，我们也常有样本方差估计总体方差