




- 沪科版数学八年级下册 20.2 数据的集中趋势与离散程度-1.数据的集中趋势-第3课时 中位数与众数【教学课件】 课件 0 次下载
- 沪科版数学八年级下册 20.2 数据的集中趋势与离散程度-1.数据的集中趋势-第4课时 用样本平均数估计总体平均数【教学课件】 课件 0 次下载
- 沪科版数学八年级下册 20.2 数据的集中趋势与离散程度-2.数据的离散程度-第2课时 用样本的平均数、方差估计总体的平均数、方差【教学课件】 课件 0 次下载
- 沪科版数学八年级下册 20.3 综合与实践 体重指数【教学课件】 课件 0 次下载
- 沪科版数学八年级下册 第20章 数据的初步分析-章末复习【教学课件】 课件 0 次下载
沪科版八年级下册20.2 数据的集中趋势与离散程度教学课件ppt
展开两台机床都生产直径为(20±0.2)mm 的零件,为了检验产品质量,从产品中各抽出10个进行测量,结果如下(单位:mm)机床 A:20.0 19.8 20.1 20.2 19.9 20.0 20.2 19.8 20.2 19.8机床 B:20.0 20.0 19.9 20.0 19.9 20.2 20.0 20.1 20.1 19.8
要比较,首先想到比较两组数据的平均值:
从数据集中趋势这个角度很难区分两台机床生产的零件精度的稳定性. 这时需要考察数据的离散程度.
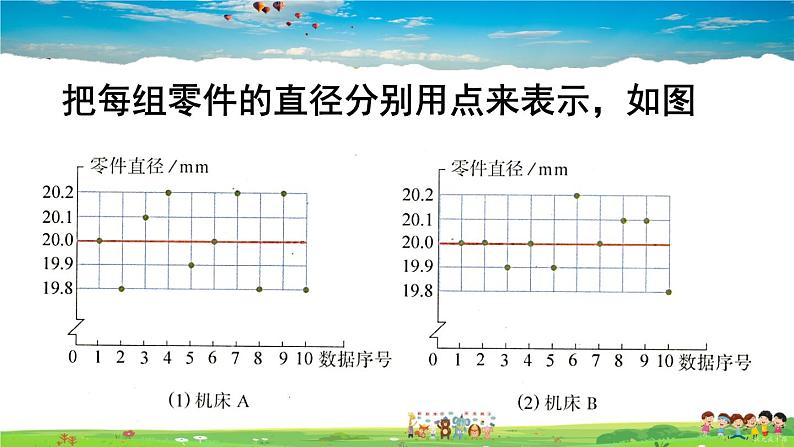
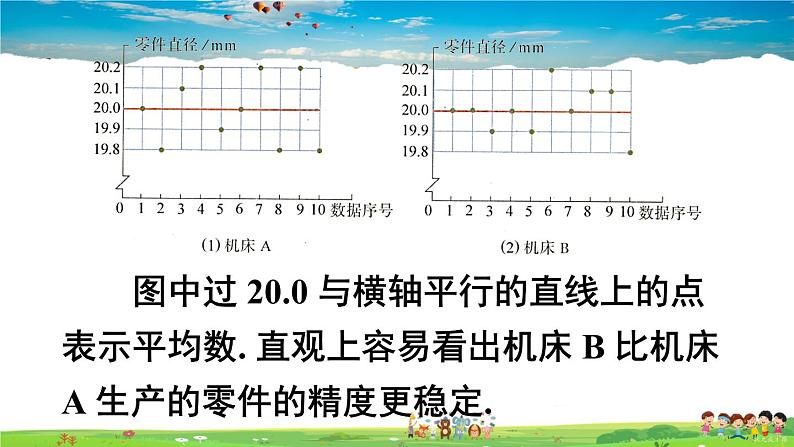
把每组零件的直径分别用点来表示,如图
图中过 20.0 与横轴平行的直线上的点表示平均数. 直观上容易看出机床 B 比机床A 生产的零件的精度更稳定.
统计学中常用下面的做法:
设一组数据是 x1,x2,…,xn,它们的平均数是
来衡量这组数据的离散程度,并把它叫做这组数据的方差,记作 s2 .
方差可以反映数据的波动程度;方差越大,说明数据的波动越大;方差越小,说明数据的波动越小.
下面通过计算方差,来评判问题中机床 A 和机床 B 哪台生产的零件的精度更稳定.
由于 0.026 > 0.012,可知机床 A 生产的 10 个零件直径比机床 B 生产的 10 个零件直径波动要大.
例 考察甲、乙两种小麦的长势,分别从中抽取 10 株苗,测得苗高如下(单位:cm):甲:12,13,14,15,10,16,13,11,15,11;乙:11,16,17,14,13,19,6,8,10,16.计算甲、乙两组数据的方差,说明哪种小麦长得较整齐.
因为 s甲2 < s乙2,所以甲种小麦长得比较整齐.
1.开机之后按[MODE],[1]进入统计模式; 2.依次按[1],[M+],[2],[M+],……,[4],[M+],5,[M+],输入数据; 3.按[RCL],[÷]即求出该样本的标准差,需要方差的话只需要将结果平方即可.
1. 如果一组数据 a1,a2,…,an 的平均数为 ,方差为 s2,那么,另一组数据 a1+2,a2+2,…,an+2 的平均数为 ,方差为 .
2. 如果一组数据 b1,b2,…,bn 的平均数为 4,方差为 ,那么另一组数据 的平均数为 ,方差为 .
1. 将一组数据中的每一个数据都加上(或减去)同一个常数,所得的一组新数据的方差不变.
2. 将一组数据中的每一个数据都变为原来的 k倍,所得的一组新数据的方差变为原数据方差的 k2 倍.
1.已知一个样本的方差 ,则这个样本的容量为 ,平均数为 .
2.甲、乙两名运动员进行了 5 次跳远的成绩测试,且知 s2甲 = 0.016,s2乙 = 0.025,由此可知 的成绩比 的成绩稳定.
3.九年级两名男同学在体育课上各练习 10 次立定跳远,平均成绩均为 2.20 m,要判断哪一名同学的成绩比较稳定,通常需要比较这两名同学立定跳远成绩的 ( )A.方差 B.众数 C. 平均数 D.中位数
4.甲、乙两台机床生产同种零件,10 天出的次品个数分别是:甲:0,1,0,2,2,0,3,1,2,4乙:2,3,1,2,0,2,1,1,2,1分别计算出两个样本的平均数和方差,根据你的计算判断哪台机床的性能较好?
方差是用来衡量一组数据的波动大小的特征量.
方差越大,数据的波动越大;方差越小,数据的波动越小,通过比较方差的大小来判断数据的稳定性.
沪科版八年级下册20.2 数据的集中趋势与离散程度作业ppt课件: 这是一份沪科版八年级下册20.2 数据的集中趋势与离散程度作业ppt课件,共9页。
初中数学20.2 数据的集中趋势与离散程度作业课件ppt: 这是一份初中数学20.2 数据的集中趋势与离散程度作业课件ppt,共12页。
初中数学沪科版八年级下册20.2 数据的集中趋势与离散程度作业课件ppt: 这是一份初中数学沪科版八年级下册20.2 数据的集中趋势与离散程度作业课件ppt,共11页。













