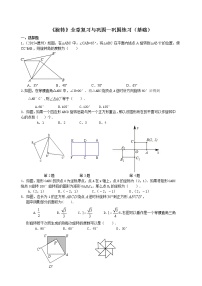
- 图形的相似和比例线段--巩固练习(提高) 试卷 8 次下载
- 相似三角形的判定--知识讲解(基础) 学案 9 次下载
- 相似三角形的判定--知识讲解(提高) 学案 9 次下载
- 相似三角形的判定--巩固练习(提高) 试卷 17 次下载
- 相似三角形的性质及应用--知识讲解(基础) 学案 11 次下载
人教版九年级下册第二十七章 相似27.2 相似三角形27.2.1 相似三角形的判定精品同步达标检测题
展开【巩固练习】
一、选择题
1. 下列判断中正确的是( ).
A.全等三角形不一定是相似三角形 B.不全等的三角形一定不是相似三角形
C.不相似的三角形一定不全等 D.相似三角形一定不是全等三角形
2.已知△ABC的三边长分别为、、 2, △A′B′C′的两边长分别是1和, 如果△ABC与△A′B′C′ 相似, 那么△A′B′C′ 的第三边长应该是 ( ).
A. B. C. D.
3.(2015•大庆校级模拟)如图,小正方形的边长均为1,则下列图形中的三角形(阴影部分)与△ABC相似的是( )
A. B. C. D.
4. (2016•盐城)如图,点F在平行四边形ABCD的边AB上,射线CF交DA的延长线于点E,在不添加辅助线的情况下,与△AEF相似的三角形有( )
A.0个B.1个C.2个D.3个
5.在矩形ABCD中,E、F分别是CD、BC上的点,若∠AEF=90°,则一定有( ).
A.ΔADE∽ΔAEF B.ΔECF∽ΔAEF C.ΔADE∽ΔECF D.ΔAEF∽ΔABF
6. 如图所示在平行四边形ABCD中,EF∥AB,DE:EA=2:3,EF=4,则CD的长为( ).
A. B.8 C.10 D.16
二、填空题
7. (2016•娄底)如图,已知∠A=∠D,要使△ABC∽△DEF,还需添加一个条件,你添加的条件是 .(只需写一个条件,不添加辅助线和字母)
8如图所示,∠C=∠E=90°,AD=10,DE=8,AB=5,则AC=________.
9.如图所示,在直角坐标系中有两点A(4,0),B(0,2),如果点C在x轴上(C与A不重合),当点C的坐标为________或________时,使得由点B、O、C组成的三角形与△AOB相似(至少找出两个满足条件的点的坐标).
10.如图,已知AB⊥BD,ED⊥BD,C是线段BD的中点,且AC⊥CE,ED=1,BD=4,那么AB=__________.
11.如图,CD∥AB,AC、BD相交于点O,点E、F分别在AC、BD上,且EF∥AB,则图中与△OEF相似的三角形为_________.
12.如图,点E是平行四边形ABCD的边BC延长线上一点,连接AE交CD于点F,则图中相似三角形共有_________对.
三.解答题
13. 如图,在△ABC中,DE∥BC,AD=3,AE=2,BD=4,求的值及AC、EC的长度.
14. 如图在梯形ABCD中,AD∥BC,∠A=90°,且,求证:BD⊥CD.
15.(2014秋•射阳县校级月考)如图,在△ABC中,已知∠BAC=90°,AD⊥BC于D,E是AB上一点,AF⊥CE于F,AD交CE于G点,
(1)求证:AC2=CE•CF;
(2)若∠B=38°,求∠CFD的度数.
【答案与解析】
一.选择题
1.【答案】C.
2.【答案】A.
【解析】根据三边对应成比例,可以确定,所以第三边是
3.【答案】B.
【解析】已知给出的三角形的各边AB、CB、AC分别为、2、、
只有选项B的各边为1、、与它的各边对应成比例.故选B.
4.【答案】C.
【解析】∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥DC,
∴△AEF∽△CBF,△AEF∽△DEC,
∴与△AEF相似的三角形有2个.
5.【答案】C.
【解析】∵∠AEF=90°, ∴∠1+∠2=90°,又∵∠D=∠C=90°,∴∠3+∠2=90°, 即∠1=∠3,∴△ADE∽△ECF.
6.【答案】C.
【解析】∵ EF∥AB,∴ , ∵ ,∴ ,,
∴ CD=10,故选C.
二. 填空题
7.【答案】AB∥DE.
【解析】∵∠A=∠D,
∴当∠B=∠DEF时,△ABC∽△DEF,
∵AB∥DE时,∠B=∠DEF,
∴添加AB∥DE时,使△ABC∽△DEF.
8.【答案】 3 .
【解析】∵ ∠C=∠E,∠CAB=∠EAD,∴ △ACB∽△AED,
∴ ,BC=4,
在Rt△ABC中,.
9.【答案】; .
10.【答案】4.
【解析】∵AB⊥BD,ED⊥BD,∴∠B=∠D=90°,又∵AC⊥CE,∴∠BCA+∠DCE=90°,
∴∠BCA=∠E,∴△ABC∽△CDE.
∵C是线段BD的中点,ED=1,BD=4
∴BC=CD=2
∴,即AB=4.
11.【答案】△OAB,△OCD.
12.【答案】3.
【解析】∵平行四边形ABCD,∴AD∥BE.AB∥CD
∴△EFC∽△EAB; △EFC∽△AFD; △AFD∽△EAB.
三 综合题
13.【解析】∵DE∥BC,∴△ADE∽△ABC,
∵,,∴,∴AC=,∴EC=AC-AE=.
14.【解析】∵AD∥BC,∴∠ADB=∠DBC,
又∵,∴△ABD∽△DCB, ∴∠A=∠BDC,
∵∠A=90°,∴∠BDC=90°,∴BD⊥CD .
15.【解析】解:(1)∵AD⊥BC,
∴∠CFA=90°,
∵∠BAC=90°,
∴∠CFA=∠BAC,
∵∠ACF=∠FCA,
∴△CAF∽△CEA,
∴=,
∴CA2=CE•CF;
(2)∵∠CAB=∠CDA,∠ACD=∠BCA,
∴△CAD∽△CBA,
∴=,
∴CA2=CB×CD,
同理可得:CA2=CF×CE,
∴CD•BC=CF•CE,
∴=,
∵∠DCF=∠ECB,
∴△CDF∽△CEB,
∴∠CFD=∠B,
∵∠B=38°,
∴∠CFD=38°.
人教版九年级数学下册基础知识专项讲练 专题27.17 相似三角形的判定(巩固篇)(专项练习): 这是一份人教版九年级数学下册基础知识专项讲练 专题27.17 相似三角形的判定(巩固篇)(专项练习),共32页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
人教版九年级下册第二十七章 相似综合与测试精品习题: 这是一份人教版九年级下册第二十七章 相似综合与测试精品习题,共6页。
人教版九年级下册27.2.1 相似三角形的判定优秀课时训练: 这是一份人教版九年级下册27.2.1 相似三角形的判定优秀课时训练,共6页。