湘教版八年级上册第2章 三角形2.5 全等三角形教课ppt课件

这是一份湘教版八年级上册第2章 三角形2.5 全等三角形教课ppt课件，共27页。PPT课件主要包含了学习目标，“边边边”判定方法，几何语言，∴∠B∠D，∴∠A∠D，ABDC，ACDF，BCCF，∴BCCF，针对训练等内容，欢迎下载使用。

1.掌握判定三角形全等的“边边边”的条件，并会运用；（重点、难点）2.全面掌握三角形的稳定性，并会运用三角形的稳定性去解决实际问题.
拿三根火柴棍首尾相接地搭三角形，你能搭出几种呢？试试看．　
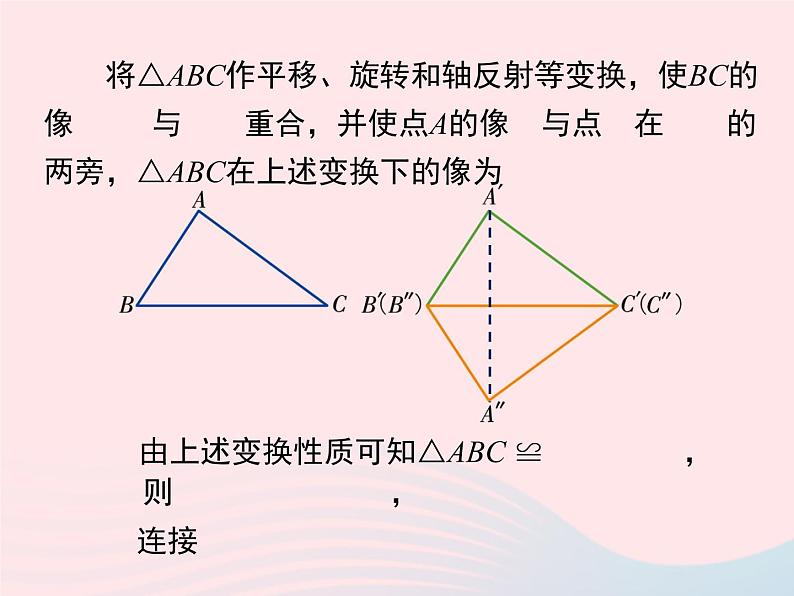
如图，在△ABC和△A′B′C′中，如果AB=A′B′，BC= B′C′，AC= A′C′ ，那么△ABC与△A′B′C′全等吗？
如果能够说明∠A=∠A′，那么就可以由“边角边”得出△ABC≌△A′B′C′.
由上述变换性质可知△ABC ≌ ，
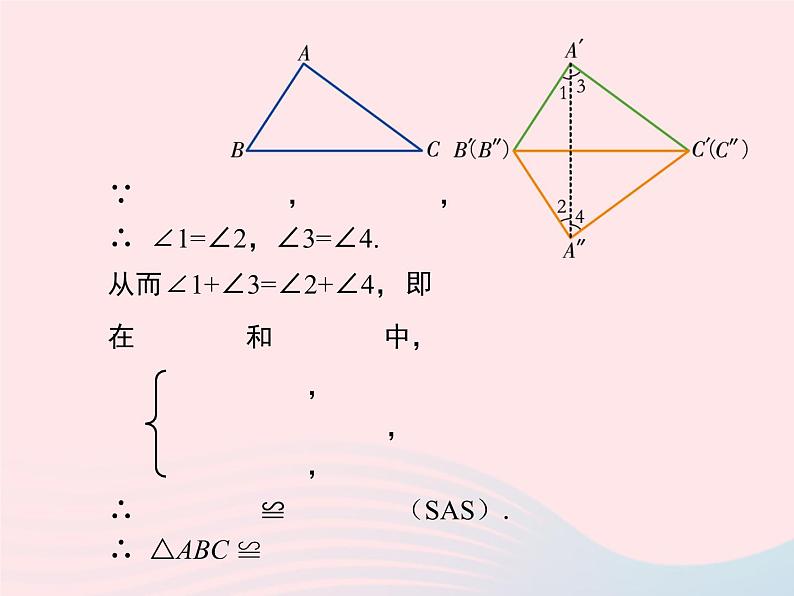
∴ ∠1=∠2，∠3=∠4.
从而∠1+∠3=∠2+∠4，
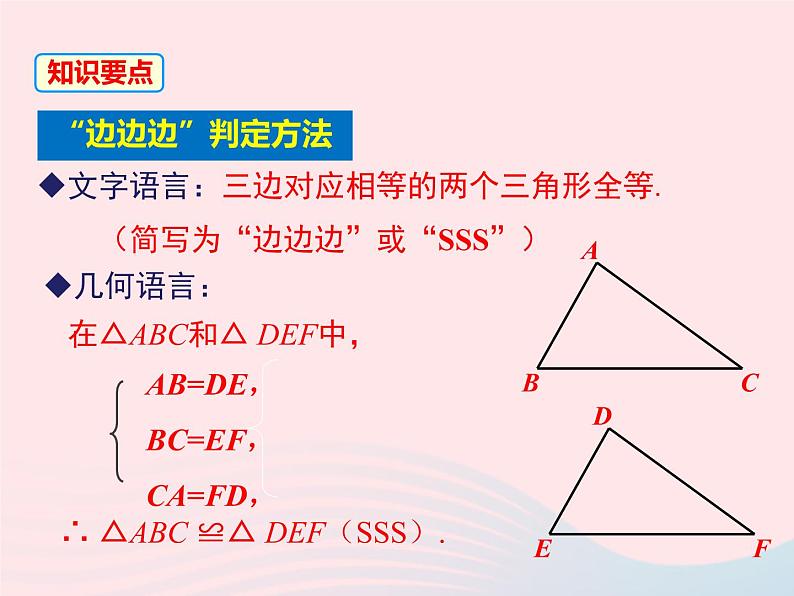
文字语言：三边对应相等的两个三角形全等. （简写为“边边边”或“SSS”）
在△ABC和△ DEF中，
∴ △ABC ≌△ DEF（SSS）.
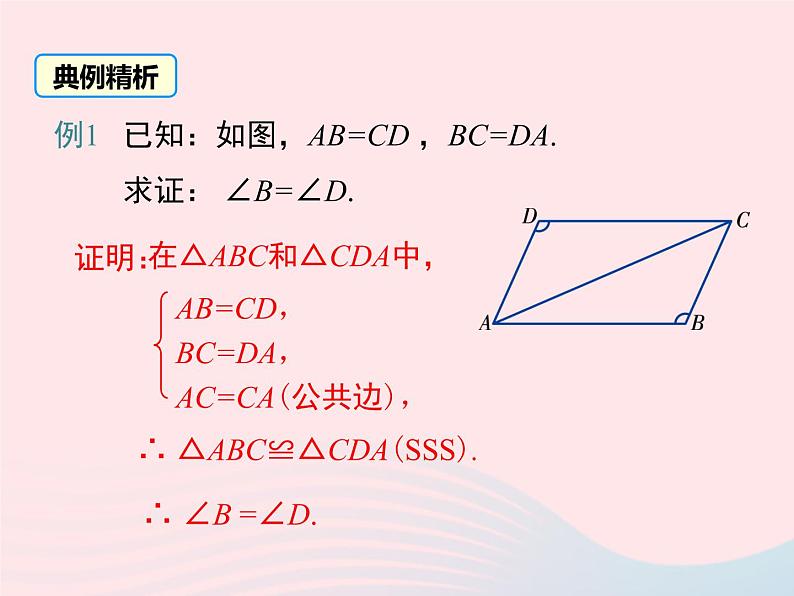
例1 已知：如图，AB=CD ，BC=DA. 求证： ∠B=∠D.
∴ △ABC≌△CDA(SSS).
例2 已知：如图，AC与BD相交于点O，且AB=DC， AC=DB．求证：∠ A=∠D．
在△ABC和△DCB中，
∴ △ABC≌△DCB（SSS）.
例3 已知：如图，在△ABC中，AB=AC，点D，E在BC上，且AD=AE，BE=CD.求证：△ABD≌△ACE.
证明 ∵ BE = CD，
∴ BE-DE = CD-DE.
即 BD = CE.
在△ABD和△ACE中，
∴ △ABD≌△ACE （SSS）.
如图, C是BF的中点，AB =DC,AC=DF.求证:△ABC ≌ △DCF.
在△ABC 和△DCF中，
∴ △ABC ≌ △DCF
证明：∵C是BF中点，
已知: 如图,点B、E、C、F在同一直线上 , AB = DE , AC = DF ,BE = CF .求证: （1）△ABC ≌ △DEF
∴ △ABC ≌ △DEF ( SSS )
在△ABC 和△DEF中
AB = DEAC = DFBC = EF
∴ BE+EC = CF+CE
（2）∵ △ABC ≌ △DEF（已证） ∴ ∠A=∠D（全等三角形对应角相等）
(1)将三根木条用钉子钉成一个三角形木架，然后扭动它，你能发现什么？
(2)将四根木条用钉子钉成一个四边形木架，然后扭动它，你能发现什么？
(3)在四边形木架上再钉上一根木条，将它的一对顶点连接起来，然后再扭动它，看看有什么变化？
四边形木架会变形，但三角形的木架能固定住.
三角形这个性质的叫作三角形的稳定性.
“只要三角形三条边的长度固定，这个三角形的形状和大小也就完全确定，三角形的这种性质叫做“三角形的稳定性”.这就是说，三角形的稳定性不是“拉得动、拉不动”的问题，其实质应是“三角形边长确定，其形状和大小就确定了”.
你能举出一些现实生活中的应用了三角形稳定性的例子吗?
观察上面这些图片，你发现了什么？
这说明三角形有它所独有的性质，是什么呢？我们通过实验来探讨三角形的特性.
发现这些物体都用到了三角形，为什么呢？
1.下列图形中哪些具有稳定性.
2.如图，工人师傅砌门时，常用木条EF固定门框ABCD，使其不变形，这种做法的根据是( )
A.两点之间线段最短B.三角形两边之和大于第三边C.长方形的四个角都是直角D.三角形的稳定性
1.如图，D、F是线段BC上的两点，AB=CE，AF=DE， 要使△ABF≌△ECD，还需要条件 ___ .
BF=CD（答案不唯一）
2.如图，AB＝CD，AD＝BC, 则下列结论： ①△ABC≌△CDB；②△ABC≌△CDA；③△ABD ≌△CDB；④BA∥DC. 正确的个数是 ( ) A . 1个 B. 2个 C. 3个 D. 4个
3.如图，桥梁的斜拉钢索是三角形的结构，主要是为了 ( ) A.节省材料,节约成本 B.保持对称 C.利用三角形的稳定性 D美观漂亮
4.已知：如图 ，AC=FE，AD=FB,BC=DE.求证：(1)△ABC≌△FDE; (2) ∠C= ∠E.
证明：(1)∵ AD=FB， ∴AB=FD（等式性质）. 在△ABC和△FDE 中，
AC=FE（已知），BC=DE（已知），AB=FD（已证），∴△ABC≌△FDE（SSS）；
(2) ∵ △ABC≌△FDE（已证）.
∴ ∠C=∠E（全等三角形的对应角相等）.
5.如图，AB＝AC，BD＝CD，BH＝CH，图中有几组全等的三角形？它们全等的条件是什么？
△ABD≌△ACD(SSS)
△ABH≌△ACH(SSS)
△BDH≌△CDH(SSS)