人教版七年级上册3.3 解一元一次方程（二）----去括号与去分母获奖课件ppt

这是一份人教版七年级上册3.3 解一元一次方程（二）----去括号与去分母获奖课件ppt，共28页。PPT课件主要包含了复习提问，②找找出相等关系，③列列出方程，④解求出方程的解，该方程与上节课的方程，在结构上有什么不同，怎样才能将方程，转化为，的形式呢，问题5等内容，欢迎下载使用。

运用方程解实际问题的步骤是什么？
①设：设出合理的未知数
把一些图书分给某班同学阅读，如果每人3本，则剩余20本；若每人4本，则还缺少25本，这个班的学生有多少人？
这批书共有（3x+20）本
这批书共有（4x－25）本
表示同一个量的两个不同的式子相等（即：这批书的总数是一个定值）
3x+20=4x－25
尝试合作, 探究方法
2、使方程左边不含常数项
3x+20－4x=4x－25－4x
3x+20－4x=－25
3x+20－4x－20=－25－20
3x－4x=－25－20
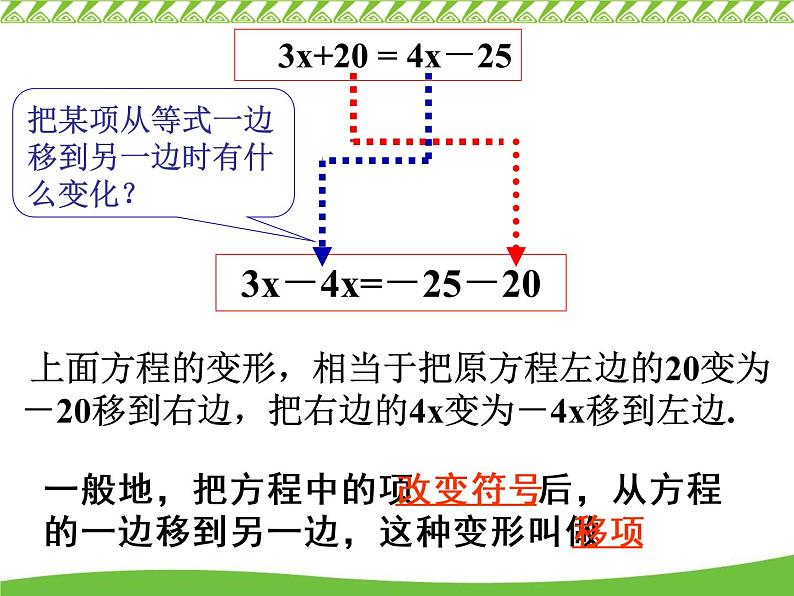
3x+20 = 4x－25
上面方程的变形，相当于把原方程左边的20变为－20移到右边，把右边的4x变为－4x移到左边.
把某项从等式一边移到另一边时有什么变化？
一般地，把方程中的项改变符号后，从方程的一边移到另一边，这种变形叫做移项
上面解方程中“移项”起到了什么作用？
通过移项，含未知数的项与常数项分别位于方程左右两边，使方程更接近于 的形式.
注：一般的我们把含未知数的项移到等号的左边，把常数项移到等号的右边。
 请你判断 
下列方程变形是否正确？
⑴6－x=8，移项得x－6=8⑵6+x=8，移项得x=8+6⑶3x=8－2x，移项得3x+2x=－8(4)5x－2=3x+7,移项得5x+3x=7+2
－ x = 8 - 6
3x + 2x = 8
5x － 3x = 7+2
例4 某制药厂制造一批药品，如用旧工艺，则废水排量要比环保限制的最大量还多200t；如用新工艺，则废水排量比环保限制的最大量少100t.新、旧工艺的废水排量之比为2︰5，两种工艺的废水排量各是多少？
练习 解下列方程
解析：选D，以总人数为不变的量由题意得
以下是两种移动电话计费方式：
（1）一个月内在本地通话200分和350分，按方式一需交费多少元？按方式二需交费多少元？
当通话时间为200分钟时:
当通话时间为350分钟时： 方式一需交费135 元，方式二需交费140 元.
对于方式一，话费等于“月租费”加“通话费”，所以话费为：
对于某个本地通话时间，会出现按两种计费方式收费一样多的情况吗？此时通话时间是多少分？
(2)设累计通话 t 分，则按方式一要收费 (30+0.3t) 元，按方式二要收费 0.4t 元，如果两种计费方式的收费一样，则
由上可知，如果一个月内通话300分，那么两种计费方式的收费相同.
两种移动电话计费方式表
(1)一个月内在本地通话200分和300分,按两种计费方式各须交费多少元?(2)对于某个本地通话时间,会出现两种计费方式的收费一样的情况吗?
交费=月租费＋当月通话时间×单价(元/分)
(2)设累计通话t分钟,则用“全球通”要收费(50＋0.4t)元,用“神州行”要收费0.6t。如果两种收费一样，则0.6t=50＋0.4t解此方程得: 0.2t=50∴ t=250答:如果一个月内通话250分,那么两种计费方式相同.
问题:什么情况下用“全球通”优惠一些?什么情况下用“神州行”优惠一些?
数学问题（一元一次方程）
数学问题的解 （x=a）
移项 （等式性质1） 合并同类项
系数化为1 （等式性质2）
2. 列方程解应用题的步骤:
二.分析题意找出等量关系：
三.根据等量关系列方程：
小明想在两种灯中选购一种,其中一种是11瓦(即0.011千瓦)的节能灯,售价60元;另一种是60瓦(即0.06千瓦)的白炽灯,售价3元.两种灯的照明效果一样,使用寿命也相同(3000小时以上).节能灯售价较高,但是较省电;白炽灯售价低,但是用电多.如果电费是0.5元/(千瓦时),选哪种灯可以节省费用(灯的售价加电费)?
分析:问题中有基本等量关系:费用=灯的售价＋电费;电费=0.5×灯的功率(千瓦) ×照明时间(时).
(1)设照明时间为t小时,则
(2)用特殊值试探:如果取 t=2000时,
节能灯的总费用为:60＋0.5×0.011t =60＋0.5×0.011×2000=71;白炽灯的总费用为:3＋0.5×0.06t =3＋0.5×0.06×2000=63;
60＋0.5×0.011t
3＋0.5×0.06t
由两组数值可以说明,照明时间不同,为了省钱而选择用哪种灯的答案也不同.
如果取t=2500呢?请你算一算节能灯与白炽灯哪个费用较低?
解:设照明时间为t小时,则节能灯的总费用为[60＋0.5×0.011t]元;白炽灯的总费用为[3＋0.5×0.06t]元;如果两个总费用相等,则有60＋0.5×0.011t =3＋0.5×0.06t解此方程得:t≈2327(小时)因此我们可以取t=2000小时和t=2500小时,分别计算节能灯和白炽灯的总费用
当t=2000时,节能灯的总费用为:60＋0.5×0.011t =60＋0.5×0.011×2000=71;白炽灯的总费用为:3＋0.5×0.06t =3＋0.5×0.06×2000=63;当t=2500时,节能灯的总费用为:60＋0.5×0.011×2500=73.75;白炽灯的总费用为:3＋0.5×0.06×2500=78;
因此由方程的解和试算判断: 在t<2327小时时,选择白炽灯优惠一些;在t=2327小时时,两种等的总费用一样;在t>2327小时而不超过使用寿命时,选择节能灯优惠一些.
问题: 如果灯的使用寿命都是3000小时,而计划照明3500小时,则需要购买两个灯,试设计你认为能省钱的选灯方案.