初中数学苏科版八年级上册3.1 勾股定理精品ppt课件

这是一份初中数学苏科版八年级上册3.1 勾股定理精品ppt课件，共22页。PPT课件主要包含了＜x＜14等内容，欢迎下载使用。

3.1　勾股定理（1）
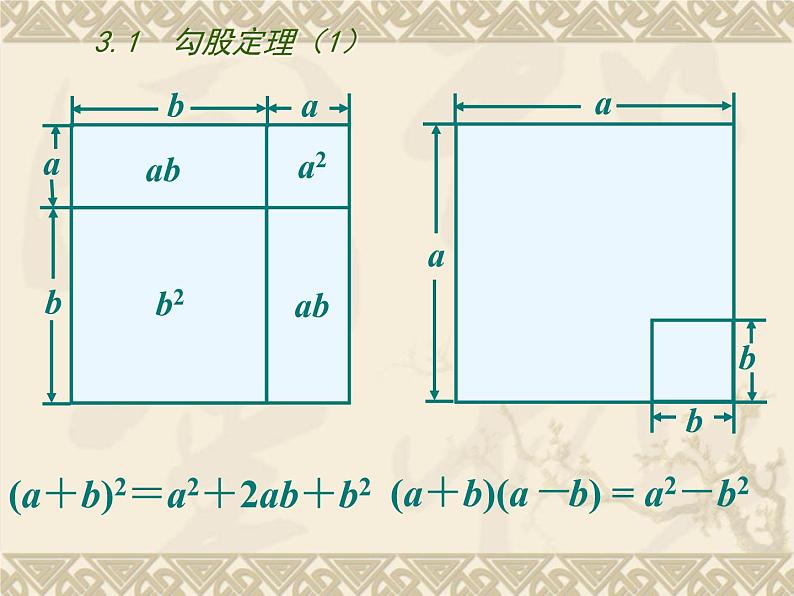
(a＋b)2＝a2＋2ab＋b2
(a＋b)(a－b) = a2－b2
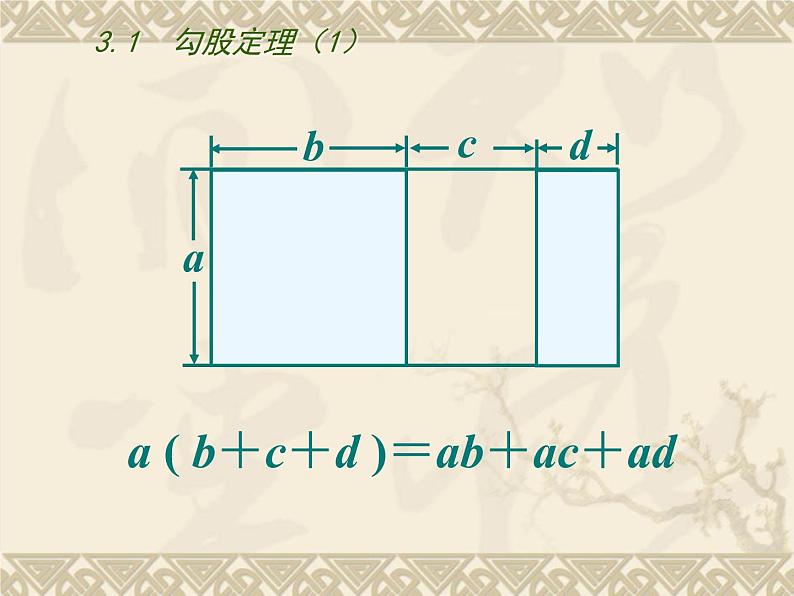
a ( b＋c＋d )＝ab＋ac＋ad
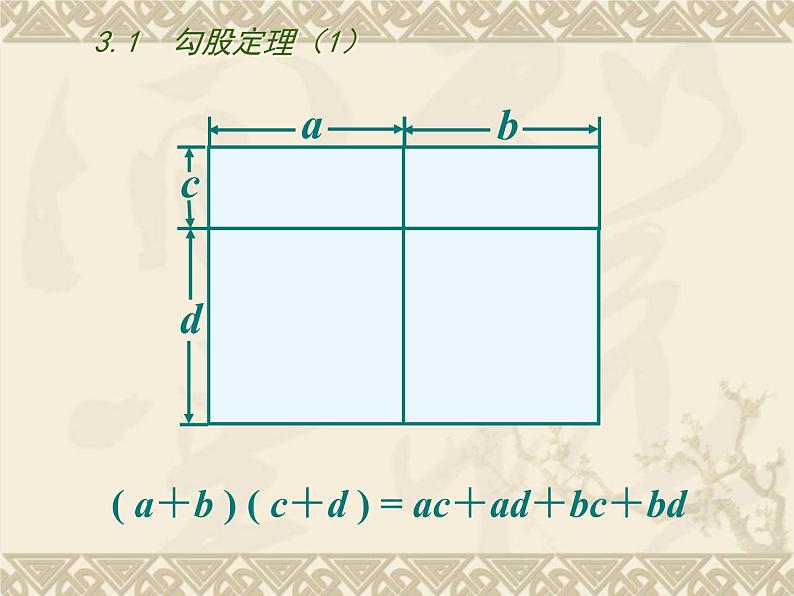
( a＋b ) ( c＋d ) = ac＋ad＋bc＋bd
勾股史话 我国是最早了解勾股定理的国家之一．早在三千多年前，周朝的数学家商高就提出，将一根直尺折成一个直角，如果勾等于三，股等于四，那么弦就等于五，即“勾三、股四、弦五”．它被记载于我国古代著名的数学著作《周髀算经》中．在这本书中的另一处，还记载了勾股定理的一般形式．这一发现，至少早于古希腊人500多年．作为一名中国人，我们应为我国古人的博学和多思而感到自豪！　
勾股定理是人类文明的成果，几乎所有拥有古代文化的民族和国家都对勾股定理有所研究．在地球以外是否存在生命这个问题上，我国数学家华罗庚曾认为，如果外星人也拥有文明的话，我们可以用“勾股定理”的图形，作为人类探寻“外星人”并与“外星人”联系的“语言”．
1．求下列直角三角形中未知边的长：
2．求下列图中未知数x、y、z的值：
如图，一块长约 80m、宽约 60m 的长方形草坪，被一些人沿对角线踏出了一条“捷径”，类似的现象也时有发生．请问同学们：
1．走“捷径”的客观原因 是什么？为什么？
2．“捷径”比正路近多少？
一、P82习题3.1第1、2题； 二、进入某些网页，你可以找到一些勾股定理的数据，例如定理是在什么时候被发现、定理的发现者、它们的背景、定理名称的由来、它在不同国家中的故事、它是在什么场合被发现等.    
一架消防队的梯子长25m，在一次火灾中, 梯子的底部离建筑物15m，此时，梯子最高能到多少米？
　　如果每层楼高4m，要想救上一层的人，梯子的底部要向楼的方向推进多少米？
《九章算术》中的引葭(jiā) 赴岸问题：    “今有池方一丈，葭(jiā)生其中央．出水一尺，引葭赴岸，适与岸齐．问水深、葭长各几何．” 题意是：有一个边长为10尺的正方形池塘，一棵芦苇AB生长在它的中央，高出水面部分BC为1尺．如果把该芦苇沿与水池边垂直的方向拉向岸边，那么芦苇的顶部B恰好碰到岸边的B′．问水深和芦苇长各多少？
　　做一个长、宽、高分别为50厘米、40厘米、30厘米的木箱，一根长为70厘米的木棒能否放入，为什么？试用今天学过的知识说明．