初中数学人教版八年级上册12.2 三角形全等的判定一等奖课件ppt

这是一份初中数学人教版八年级上册12.2 三角形全等的判定一等奖课件ppt，共14页。PPT课件主要包含了证三角形全等，探究新知1，用符号语言表达为，探究新知2，做一做，探究新知⑵，练一练，即∠A∠D等内容，欢迎下载使用。

1、边边边公理2、转化思想证线段位置关系（垂直、平行）角平分线求角度数、数量关系
找对应相等的边：公共边、中点或中线、通过计算（同加或同减）、做辅助线（构造公共边等）
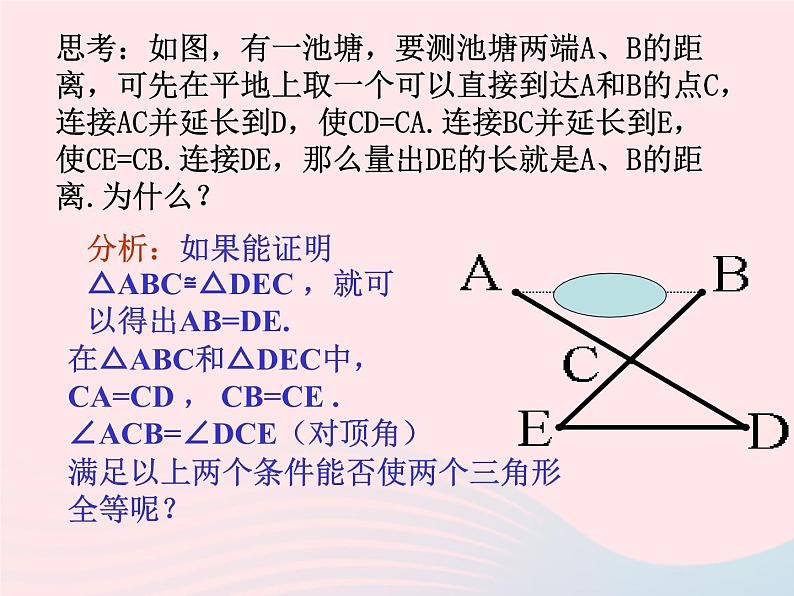
思考：如图，有一池塘，要测池塘两端A、B的距离，可先在平地上取一个可以直接到达A和B的点C，连接AC并延长到D，使CD=CA.连接BC并延长到E，使CE=CB.连接DE，那么量出DE的长就是A、B的距离.为什么？
分析：如果能证明△ABC≌△DEC ，就可以得出AB=DE.
在△ABC和△DEC中，CA=CD ， CB=CE .∠ACB=∠DCE（对顶角）满足以上两个条件能否使两个三角形全等呢？
画△ABC,使AB=3cm，AC=4cm。
2. 在射线AM上截取AB= 3cm
3. 在射线AN上截取AC=4cm
若再加一个条件，使∠A=45°，画出△ABC
1. 画∠MAN= 45°
则△ABC就是所求的三角形
把你们所画的三角形剪下来与同桌所画的三角形进行比较，它们能互相重合吗？
由前边的作图比较过程，我们可以得出什么结论？
在△ABC与△DEF中
AB=DE∠A=∠DAC=DF
∴△ABC≌△DEF（SAS）
两边和它们的夹角对应相等的两个三角形全等。简写成“边角边”或“SAS”
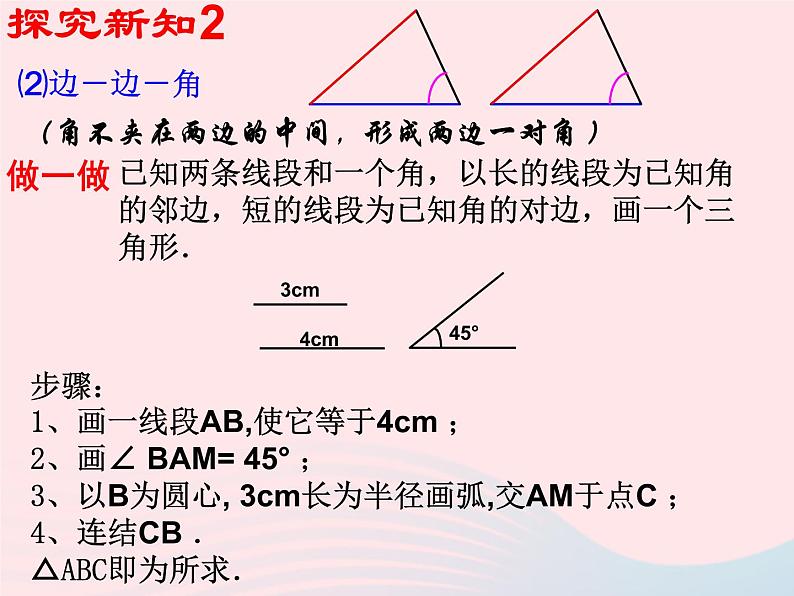
（角不夹在两边的中间，形成两边一对角 ）
已知两条线段和一个角，以长的线段为已知角的邻边，短的线段为已知角的对边，画一个三角形．
步骤：　1、画一线段AB,使它等于4cm ；2、画∠ BAM= 45° ；3、以B为圆心, 3cm长为半径画弧,交AM于点C ；4、连结CB ．△ABC即为所求．
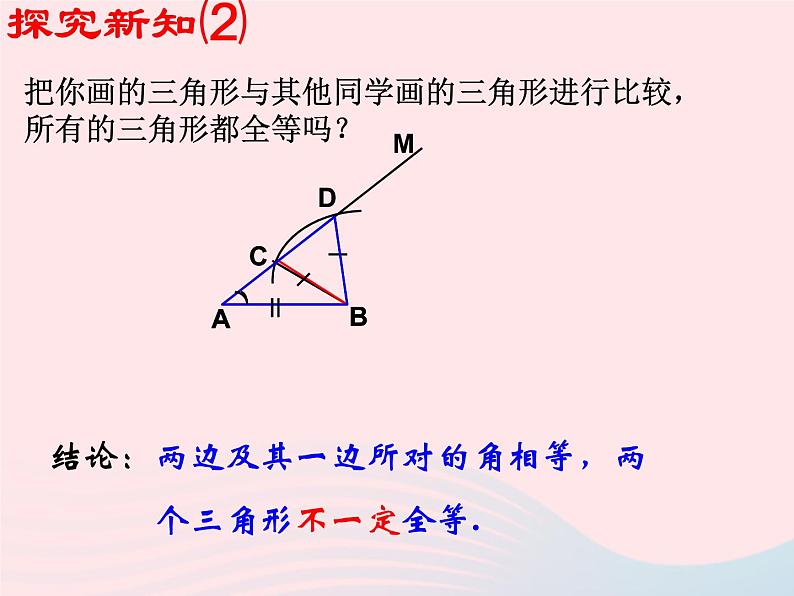
把你画的三角形与其他同学画的三角形进行比较，所有的三角形都全等吗？
结论：两边及其一边所对的角相等，两 个三角形不一定全等.
1、如图，B点在A点的正北方向。两车从路段AB的一端A出发，分别向东、向西进行相同的距离，到达C、D两地。此时C，D到B的距离相等吗？为什么？
【证明】∵在△BAD和△BAC中，
BA=BA∠BAD=∠BACAD=AC
则△BAD≌△BAC (SAS).
寻找对应相等的边角边公共边-对应边垂直-对应角（90°）中点-对应边
2、如图，点E、F在BC上，BE=CF，AB=DC， ∠B=∠C，求证： ∠A=∠D
【证明】∵BF=BE+EF CE=CF+FE 而BE=CF ∴BF=CE
在△ABF和△DCE中，
BF=CE∠B=∠CAB=DC
∴△BAD≌△BAC (SAS)
寻找对应相等的边角边相等线段同加同减-对应边
3、如图，已知AB=AE,AC=AD,∠BAD=∠EAC,证明：∠B=∠E
证明：∵ ∠BAD=∠EAC∴ ∠BAD+∠DAC=∠EAC+∠DAC 即∠BAC=∠DAE
在△ABC与△ADE中，
AB=AE∠BAC=∠DAEAD=AC
∴△ABC≌△AED ∴∠B=∠E
寻找相等的角相等的两个角同加或同减，得到相等的对应角
4、如图，AB平分∠DAC，要用SAS条件确定△ABC≌△ADB,还需要有什么条件？
寻找相等的对应角角平分线寻找相等的对应边公共边
全品P25 8题、9题
证明线段相等---先证明三角形全等（SAS)
寻找相等的对应角根据平行线的性质（内错角相等、同位角相等）直角三角形（直角）
1、边边边公理、边角边公理—夹角2、转化思想证线段位置关系（垂直、平行）角平分线求角度数、数量关系