
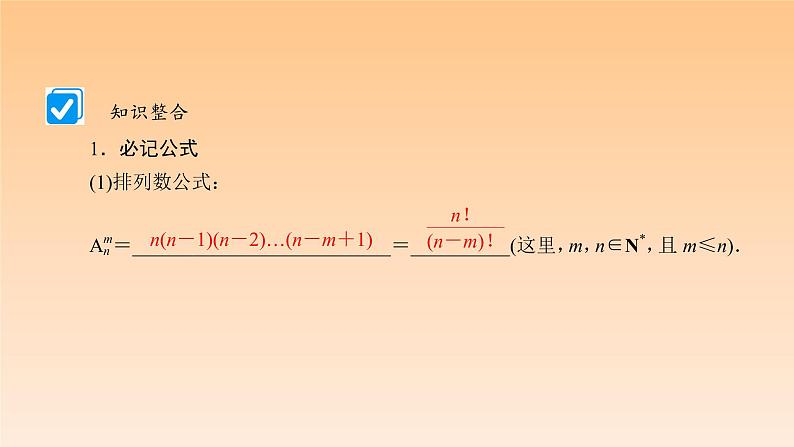





数学6.3 二项式定理复习ppt课件
展开n(n-1)(n-2)…(n-m+1)
易错警示1.分类标准不明确,有重复或遗漏,区分平均分组与平均分配问题.2.混淆排列问题与组合问题的差异.3.混淆二项展开式中某项的系数与二项式系数.4.在求展开式的各项系数之和时,忽略了赋值法的应用.
4.(2018·全国卷Ⅰ,15)从2位女生,4位男生中选3人参加科技比赛,且至少有1位女生入选,则不同的选法共有______种.(用数字填写答案)
(1)如图,小明从街道的E处出发,先到F处与小红会合,再一起到位于G处的老年公寓参加志愿者活动,则小明到老年公寓可以选择的最短路径条数为( )A.24 B.18 C.12 D.9
[解析] E→F有6种走法,F→G有3种走法,由分步乘法计数原理知,共6×3=18种走法.
(2)如果一个三位正整数“a1a2a3”满足a1
两个计数原理的应用技巧(1)在应用分类加法计数原理和分步乘法计数原理时,一般先分类再分步,每一步当中又可能用到分类加法计数原理.(2)对于复杂的两个计数原理综合应用的问题,可恰当列出示意图或表格,使问题形象化、直观化.
跟踪训练1.两人进行乒乓球比赛,先赢三局者获胜,决出胜负为止,则所有可能出现的情况(各人输赢局次的不同视为不同情况)共有( )A.10种 B.15种 C.20种 D.30种[解析] 首先分类计算假如甲赢,比分30是1种情况;比分31共有3种情况,分别是前3局中(因为第四局肯定要赢),第一或第二或第三局输,其余局数获胜;比分为32共有6种情况,就是说前4局22,最后一局获胜,前4局中,用排列方法,从4局中选2局获胜,有6种情况.甲一共就1+3+6=10种情况获胜.所以加上乙获胜情况,共有10+10=20种情况.
2.如图所示,用4种不同的颜色涂入图中的矩形A,B,C,D中,要求相邻的矩形涂色不同,则不同的涂法有( )A.72种 B.48种C.24种 D.12种
排列与组合的简单应用
(1)某次联欢会要安排3个歌舞类节目,2个小品类节目和1个相声类节目的演出顺序,则同类节目不相邻的排法种数是( )A.72种 B.120种 C.144种 D.168种
(2)数列{an}共有12项,其中a1=0,a5=2,a12=5,且|ak+1-ak|=1,k=1,2,3,…,11,则满足这种条件的不同数列的个数为( )A.84 B.168 C.76 D.152
(3)(2018·浙江卷)从1,3,5,7,9中任取2个数字,从0,2,4,6中任取2个数字,一共可以组成__________个没有重复数字的四位数.(用数字作答)
解答排列组合问题的常用方法排列组合问题从解法上看,大致有以下几种:(1)有附加条件的排列组合问题,大多需要用分类讨论的方法,注意分类时应不重不漏;(2)排列与组合的混合型问题,用分类加法或分步乘法计数原理解决;
(3)元素相邻,可以看作是一个整体的方法;(4)元素不相邻,可以利用插空法;(5)间接法,把不符合条件的排列与组合剔除掉;(6)穷举法,把符合条件的所有排列或组合一一写出来;(7)定序问题缩倍法;(8)“小集团”问题先整体后局部法.
跟踪训练1.(2017·全国卷Ⅱ,6)安排3名志愿者完成4项工作,每人至少完成1项,每项工作由1人完成,则不同的安排方式共有( )A.12种 B.18种 C.24种 D.36种
2.将序号分别为1、2、3、4、5的5张参观券全部分给4人,每人至少1张,如果分给同一人的2张参观券连号,那么不同的分法种数是______.
(二)与二项式系数有关的问题 (1)若(x2+1)(x-2)11=a0+a1(x-1)+a2(x-1)2+…+a13(x-1)13,a1+a2+…+a13的值为( )A.0 B.-2 C.2 D.213[解析] 记f(x)=(x2+1)(x-2)11=a0+a1(x-1)+a2(x-1)2+…+a13(x-1)13,则f(1)=a0=(12+1)(1-2)11=-2,而f(2)=(22+1)(2-2)11=a0+a1+a2+…+a13,即a0+a1+a2+…+a13=0,所以a1+a2+…+a13=f(2)-f(1)=2.
(3)(a+x)(1+x)4的展开式中x的奇数次幂项的系数之和为32,则a=_____.[解析] 由已知得(1+x)4=1+4x+6x2+4x3+x4,故(a+x)(1+x)4的展开式中x的奇数次幂项分别为4ax,4ax3,x,6x3,x5,其系数之和为4a+4a+1+6+1=32,解得a=3.
1.利用二项式定理求解的两种常用思路(1)二项式定理中最关键的是通项公式,求展开式中特定的项或者特定项的系数均是利用通项公式和方程思想解决的.(2)二项展开式的系数之和通常是通过对二项式及其展开式中的变量赋值得出的,注意根据展开式的形式给变量赋值.2.在应用通项公式时,要注意以下几点:(1)它表示二项展开式的任意项,只要n与r确定,该项就随之确定;(2)Tr+1是展开式中的第r+1项,而不是第r项;(3)公式中,a,b的指数和为n,且a,b不能随便颠倒位置;(4)对二项式(a-b)n展开式的通项公式要特别注意符号问题.
统考版2024高考数学二轮专题复习第二篇必备知识为基第4讲计数原理二项式定理课件理: 这是一份统考版2024高考数学二轮专题复习第二篇必备知识为基第4讲计数原理二项式定理课件理,共25页。PPT课件主要包含了考点一,考点二,答案C,答案A,答案D,考点二二项式定理,答案B等内容,欢迎下载使用。
高考数学(理)一轮复习课件+讲义 第10章 第3讲 二项式定理: 这是一份高考数学(理)一轮复习课件+讲义 第10章 第3讲 二项式定理,文件包含高考数学理一轮复习课件第10章第3讲二项式定理pptx、高考数学理一轮复习讲义第10章第3讲二项式定理doc等2份课件配套教学资源,其中PPT共39页, 欢迎下载使用。
高考数学(理)一轮复习课件+讲义 第10章 第1讲 分类加法计数原理与分步乘法计数原理: 这是一份高考数学(理)一轮复习课件+讲义 第10章 第1讲 分类加法计数原理与分步乘法计数原理,文件包含高考数学理一轮复习课件第10章第1讲分类加法计数原理与分步乘法计数原理pptx、高考数学理一轮复习讲义第10章第1讲分类加法计数原理与分步乘法计数原理doc等2份课件配套教学资源,其中PPT共46页, 欢迎下载使用。














