数学九年级上册24.1.3 弧、弦、圆心角评课ppt课件

这是一份数学九年级上册24.1.3 弧、弦、圆心角评课ppt课件，共28页。PPT课件主要包含了垂径定理及逆定理，回顾旧知，圆弧弧，在同圆或等圆中，弦心距，课堂小结，圆心角，达标检测反思目标等内容，欢迎下载使用。

1. 能识别圆心角.2. 探索并掌握弧、弦、圆心角的关系，了解圆的中心对称性和旋转不变性.3. 能用弧，弦、圆心角的关系解决圆中的计算题、证明题.
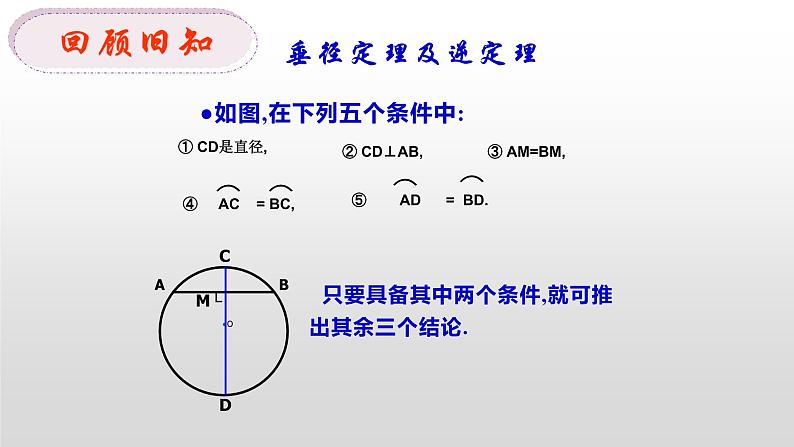
如图,在下列五个条件中:
只要具备其中两个条件,就可推出其余三个结论.
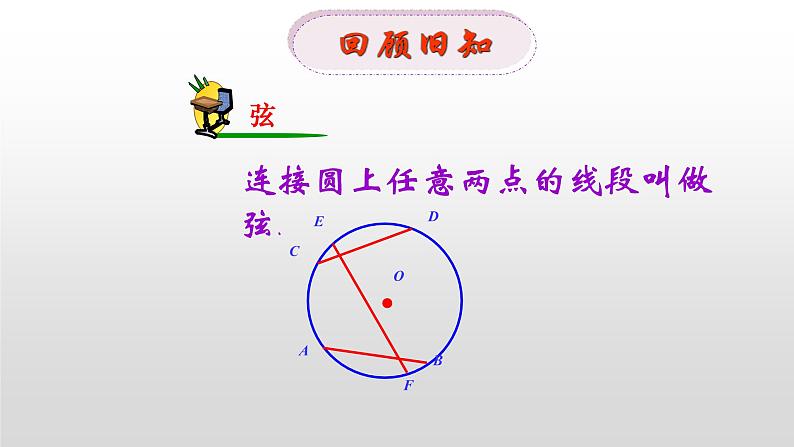
连接圆上任意两点的线段叫做弦．
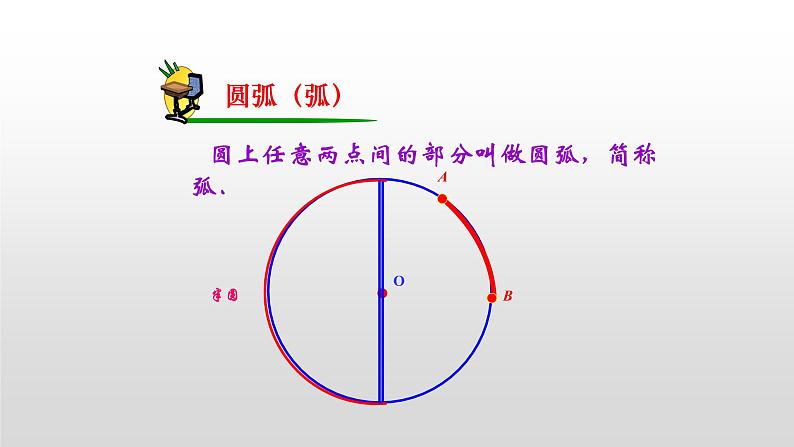
圆上任意两点间的部分叫做圆弧，简称弧．
___________
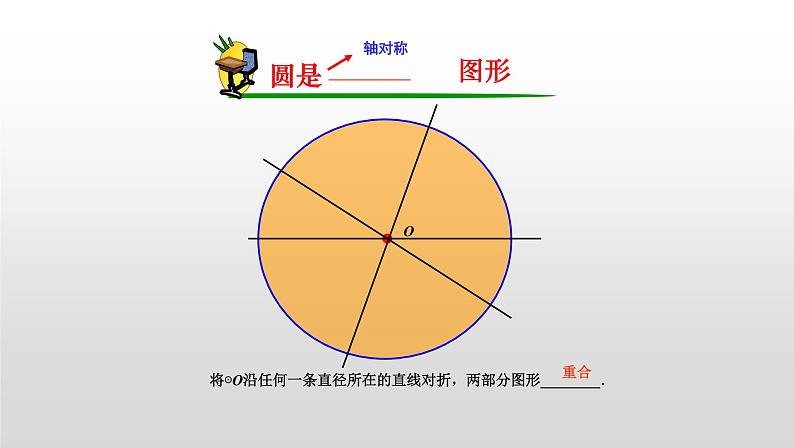
将⊙O沿任何一条直径所在的直线对折，两部分图形________．
将⊙O 绕圆心 O 顺时针旋转180°，这两个图形________．
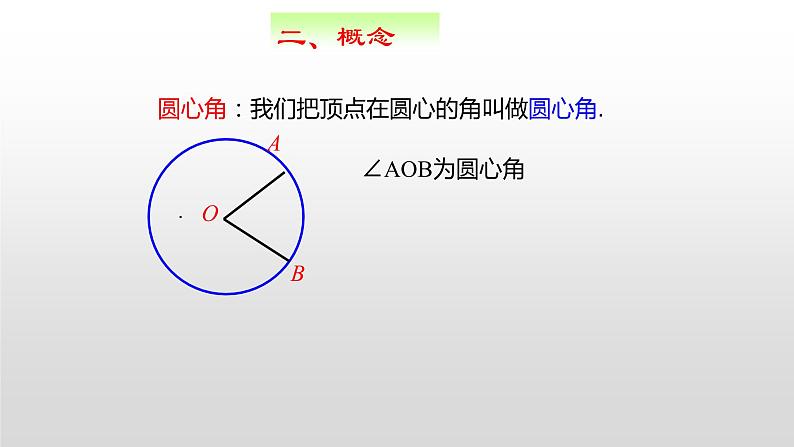
圆心角：我们把顶点在圆心的角叫做圆心角.
判一判：判别下列各图中的角是不是圆心角，并说明理由.
如图，将圆心角∠AOB绕圆心O旋转到∠A’OB’的位置，你能发现哪些等量关系？为什么？
根据旋转的性质，将圆心角∠AOB绕圆心O旋转到∠A′OB′的位置时，显然∠AOB＝∠A′OB′，射线OA与OA′重合，OB与OB′重合．而同圆的半径相等，OA=OA′，OB=OB′，从而点A与A′重合，B与B′重合．
因此， 重合，AB与A′B′重合．
同样，还可以得到：在同圆或等圆中，如果两条弧相等，那么它们所对的圆心角_____， 所对的弦________；在同圆或等圆中，如果两条弦相等，那么他们所对的圆心角______，所对的弧_________．
这样，我们就得到下面的定理：
∵∠AOB=∠A｀OB｀
想一想： 定理“在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦也相等．”中，可否把条件“在同圆或等圆中”去掉？为什么？
1.等弦所对的弧相等. （ ）
2.等弧所对的弦相等. （ ）
3.圆心角相等，所对的弦相等. ( ）
4. 如图，AB 是⊙O 的直径，　 BC = CD = DE ， ∠COD=35°，∠AOE = ．
1.如图，AB、CD是⊙O的两条弦．（1）如果AB=CD，那么___________，_________________．（2）如果 ，那么____________，______________．（3）如果∠AOB=∠COD，那么_____________，____________．
在同圆或等圆中，相等的弦所对的圆心角相等，所对的弧也相等．
弧、弦与圆心角关系定理的推论
在同圆或等圆中，如果两个圆心角、两条弧或两条弦中，有一组量相等，那么它们所对的其余各组量都分别相等。
圆心到弦的距离（即圆心到弦的垂线段的距离）．
在⊙O中，分别作相等的圆心角∠AOB和∠A′OB′，将∠AOB旋转一定角度，使OA和OA′重合．
你能发现哪些等量关系?
根据旋转的性质，∠AOB＝∠A′OB′，OA与OA′重合，OB与OB′重合． 而同圆的半径相等，OA=OA′，OB=OB′， ∴点 A与 A′重合，B与B′重合．
再根据△AOB≌△A′O′B′，
如图，⊙O与⊙O1是等圆，∠AOB =∠A1OB1，请问上述结论还成立吗？为什么?
∵ ∠AOB=∠A1OB1
在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦相等，所对的弦的弦心距相等．
①∠AOB=∠A′O′B′
弧、弦、圆心角的关系定理
(1)圆心角；(2)圆心角所对的弧；(3)圆心角所对的弦;(4)圆心角所对弦的弦心距.
其中有一组量相等，其他三组量也相等
同圆或等圆的“四量关系”定理：
∴∠AOB＝∠BOC＝∠AOC．
圆心到弦的距离（即圆心到弦的垂线段的距离）．
3． 弧、弦、圆心角的关系定理
1.已知圆O的半径为5，弦AB的长为5，则弦AB所对的圆心角∠AOB＝_______.2.在⊙O中，弦AB所对的劣弧为圆周的1/4，圆半径等于12，则圆心角∠AOB＝_____,弦AB的长为______.
3.如图，在⊙O中， ∠B＝70°，则∠A等于______.4.在⊙O中，圆心角∠AOB＝90°，点O到弦AB的的距离为4.同，则⊙O的直径长为________.