

北师大版九年级上册2 反比例函数的图象与性质课堂检测
展开一.选择题
1.反比例函数y=的图象经过点(﹣1,3),则k的值为( )
A.3B.C.﹣D.﹣3
2.下列各点在函数y=﹣的图象上的是( )
A.(2,1)B.(﹣2,0)C.(2,0)D.(﹣2,1)
3.已知点A(1,﹣3)关于x轴的对称点A′在反比例函数y=的图象上,则实数k的值是( )
A.B.3C.﹣D.﹣3
4.反比例函数y=(m为常数),在每个象限内,y随x的增大而减小,则m取值范围是( )
A.m>0B.m>2C.m<0D.m<2
5.如图,点P是反比例函数y=图象上的一个点,过P作PA⊥x轴,垂足为A,PC⊥y轴,垂足为C,则矩形OAPC的面积是( )
A.2B.C.4D.
6.如图,函数y1=x+1与函数y2=的图象相交于点M(1,m),N(﹣2,n).若y1>y2,则x的取值范围是( )
A.x<﹣2或0<x<1B.x<﹣2或x>1
C.﹣2<x<0或0<x<1D.﹣2<x<0或x>1
7.在同一平面直角坐标系中,一次函数y1=k1x+b与反比例函数y2=(x>0)的图象如图所示,则当y1>y2时,自变量x的取值范围为( )
A.x<1B.x>3C.0<x<1D.1<x<3
8.已知点A(x1,y1),B(x2,y2)在双曲线y=上,且0<x2<x1,下列选项正确的是( )
A.y1=y2B.y1>y2C.y1<y2D.无法确定
9.已知(﹣2,y1),(﹣3,y2),(2,y3)在反比例函数y=﹣图象上,则y1,y2,y3的大小关系为( )
A.y1>y2>y3B.y1>y3>y2C.y3>y2>y1D.y3>y1>y2
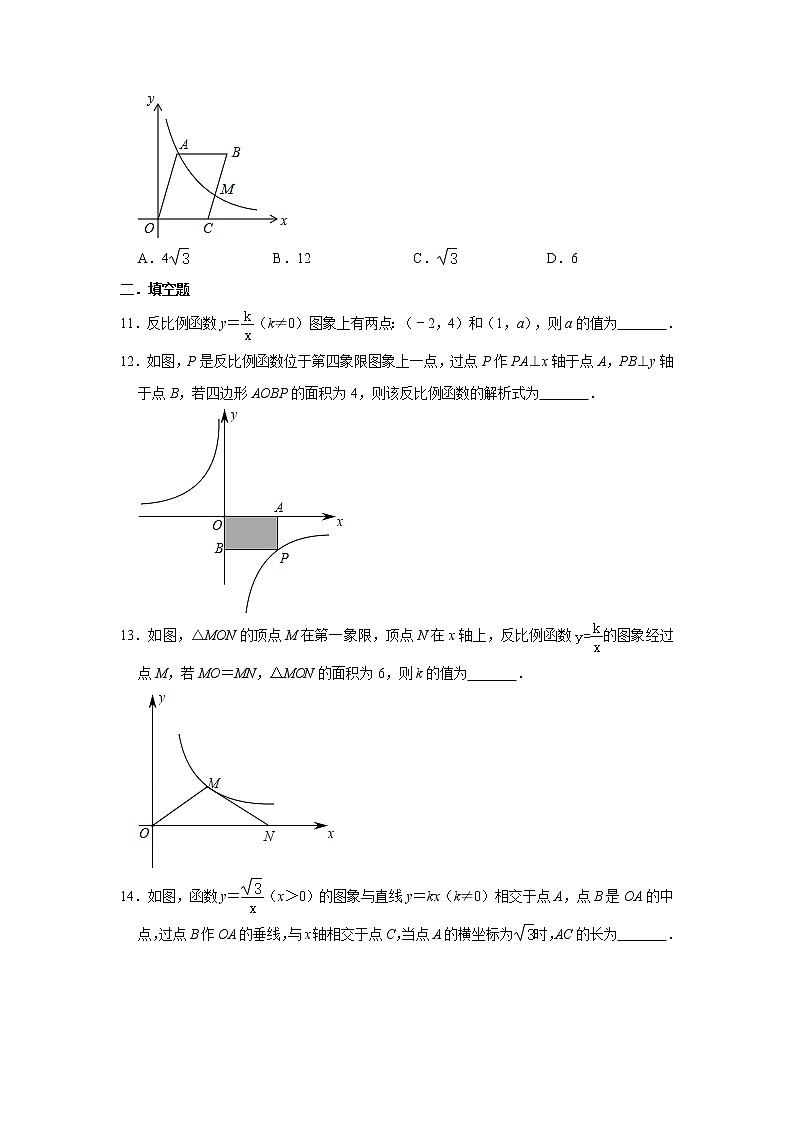
10.如图,平行四边形OABC的周长为7,∠AOC=60°,以O为原点,OC所在直线为x轴建立直角坐标系,函数y=(x>0)的图象经过▱OABC顶点A和BC的中点M,则k的值为( )
A.4B.12C.D.6
二.填空题
11.反比例函数y=(k≠0)图象上有两点:(﹣2,4)和(1,a),则a的值为 .
12.如图,P是反比例函数位于第四象限图象上一点,过点P作PA⊥x轴于点A,PB⊥y轴于点B,若四边形AOBP的面积为4,则该反比例函数的解析式为 .
13.如图,△MON的顶点M在第一象限,顶点N在x轴上,反比例函数的图象经过点M,若MO=MN,△MON的面积为6,则k的值为 .
14.如图,函数y=(x>0)的图象与直线y=kx(k≠0)相交于点A,点B是OA的中点,过点B作OA的垂线,与x轴相交于点C,当点A的横坐标为时,AC的长为 .
15.如图,已知函数y=x+3的图象与函数y=的图象交于A、B两点,连接BO并延长交函数y=的图象于点C,连接AC,若△ABC的面积为12,则k的值为 .
三.解答题
16.如图:反比例函数与一次函数的图象交于A(1,3)和B(﹣3,n)两点.
(1)求反比例函数与一次函数的解析式;
(2)当x取什么值时,一次函数的值大于反比例函数的值.
(3)求出△OAB的面积.
17.一次函数y1=kx+b与反比例函数交于点A(1,3),B(3,m).
(1)分别求两个函数的解析式;
(2)根据图象直接写出,当x为何值时,y1<y2.
参考答案
1.解:∵反比例函数y=的图象经过点(﹣1,3),
∴3=,解得k=﹣,
故选:C.
2.解:∵函数解析式为y=﹣,
把四个选项的坐标依次代入函数解析式,仅选项D的坐标(﹣2,1)在函数y=﹣的图象上,
∴D选项符合题意,A、B、C选项不符合题意,
故选:D.
3.解:∵点A(1,﹣3)和点A′关于x轴对称,
∴A′(1,3),
∵A′在反比例函数y=的图象上,
∴k=1×3=3,
故选:B.
4.解:∵反比例函数y=(m为常数),在每个象限内,y随x的增大而减小,
∴m﹣2>0,
解得,m>2,
故选:B.
5.解:∵PA⊥x轴,PC⊥y轴,
∴矩形OAPB的面积=|﹣4|=4,
故选:C.
6.解:由一次函数和反比例函数的图象可知,当一次函数图象在反比例函数图象之上时,所对应的x的取值范围为﹣2<x<0或x>1,
故选:D.
7.解:由图象可得,
当y1>y2时,自变量x的取值范围为1<x<3,
故选:D.
8.解:∵双曲线y=中k=2>0,
∴在每一个象限内,y随x的增大而减小,
∵点A(x1,y1),B(x2,y2)在双曲线y=上,且0<x2<x1,
∴y1<y2.
故选:C.
9.解:当x=﹣2时,y1=﹣=;当x=﹣3时,y2=﹣=;当x=2时,y3=﹣=﹣0.4,
所以y1>y2>y3.
故选:A.
10.解:设OA=a,OC=b,
∵▱OABC的周长为7,
∴a+b=,
∴b=﹣a,
作AD⊥x轴于D,MN⊥x轴于N,
∵∠AOC=60°,
∴OD=a,AD=a,
∴A(a,a),
∵M是BC的中点,
∴CN=a,MN=a,
∴M(﹣a+a,a),
∴a•a=(﹣a+a)•a,
解得a=2,
∴A(1,),
∴k=1×=,
故选:C.
11.解:∵点(﹣2,4)和(1,a)都在反比例函数y=(k≠0)图象上,
∴1×a=﹣2×4,解得a=﹣8.
故答案为﹣8.
12.解:∵PA⊥x轴点A,PB⊥y轴于点B,四边形AOBP的面积为4,
∴|k|=4,
∵k<0,
∴k=﹣4,
∴反比例函数的解析式为y=﹣,
故答案为y=﹣.
13.解:过M作MA⊥ON于A,
∵OM=MN,
∴ON=2OA=2AN,
设M点的坐标为(a,b),
则OA=AN=a,AM=b,ON=2a,
∵△MON的面积为6,
∴×ON•MA=×2a•b=6,
∴ab=6,
∵M在反比例函数y=上,
∴ab=k,
即k=6,
故答案为:6.
14.解:∵函数y=(x>0)的图象过点A,点A的横坐标为,
∴当x=时,y==1,
∴A(,1).
设C点坐标为(x,0),则OC=x.
∵BC是线段OA的垂直平分线,
∴OC=AC,
∴x2=(﹣x)2+(1﹣0)2,
解得x=,
∴AC=OC=,
故答案为:.
15.解:如图,连接OA.
由题意,可得OB=OC,
∴S△OAB=S△OAC=S△ABC=6.
设直线y=x+3与y轴交于点D,则D(0,3),
设A(a,a+3),B(b,b+3),则C(﹣b,﹣b﹣3),
∴S△OAB=×3×(a﹣b)=6,
∴a﹣b=4 ①.
过A点作AM⊥x轴于点M,过C点作CN⊥x轴于点N,
则S△OAM=S△OCN=k,
∴S△OAC=S△OAM+S梯形AMNC﹣S△OCN=S梯形AMNC=6,
∴(﹣b﹣3+a+3)(﹣b﹣a)=6,
将①代入,得
∴﹣a﹣b=3②,
①+②,得﹣2b=7,b=﹣,
①﹣②,得2a=1,a=,
∴A(,),
∴k=×=.
故答案为.
16.解:(1)∵把A(1,3)代入y=得:k=3,
∴反比例函数的解析式是y=,
∵把B(﹣3,n)代入y=得:n==﹣1,
∴B的坐标是(﹣3,﹣1),
∵把A、B的坐标代入y=mx+b得:,解得,
∴一次函数的解析式为y=x+2;
(2)观察函数图象知,当x>1或﹣3<x<0时,一次函数的值大于反比例函数的值;
(3)设直线AB交y轴于C,
∵把x=0代入y=x+2得:y=2,
∴OC=2,
∴△AOB的面积S=S△AOC+S△BOC=×2×1+×3×2=4.
17.解:(1)把A(1,3)代入y2=得n=1×3=3,
∴反比例函数解析式为y2=,
把B(3,m)代入y2=得3m=3,解得m=1,则B(3,1),
把A(1,3),B(3,1)代入y1=kx+b得,解得,
∴一次函数解析式为y1=﹣x+4;
(2)从图象看,当0<x<1或x>3时,y1<y2;
初中数学湘教版九年级上册1.1 反比例函数精品课时作业: 这是一份初中数学湘教版九年级上册1.1 反比例函数精品课时作业,共5页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
初中数学北师大版九年级上册第六章 反比例函数1 反比例函数精品表格综合训练题: 这是一份初中数学北师大版九年级上册第六章 反比例函数1 反比例函数精品表格综合训练题,共3页。
初中北师大版2 反比例函数的图象与性质随堂练习题: 这是一份初中北师大版2 反比例函数的图象与性质随堂练习题,共4页。试卷主要包含了2 反比例函数的图象与性质等内容,欢迎下载使用。













