
2021版高考文科数学人教通用版大一轮复习基础自查学案:4.1 平面向量的概念及其线性运算
展开温馨提示:
此套题为Word版,请按住Ctrl,滑动鼠标滚轴,调节合适的观看比例,答案解析附后。关闭Word文档返回原板块。
第四章 平面向量、数系的扩充与复数的引入
第一节 平面向量的概念及其线性运算
知识体系
必备知识
1.向量的有关概念
名称 | 定义 | 备注 |
向量 | 既有大小又有方向的量;向量的大小叫做向量的长度(或称模) | 平面向量是自由向量 |
零向量 | 长度为0的向量;其方向是任意的 | 记作0 |
单位 向量 | 长度等于1个单位的向量 | 非零向量a的单位向量为± |
平行 向量 | 方向相同或相反的非零向量 | 0与任一向量平行或共线 |
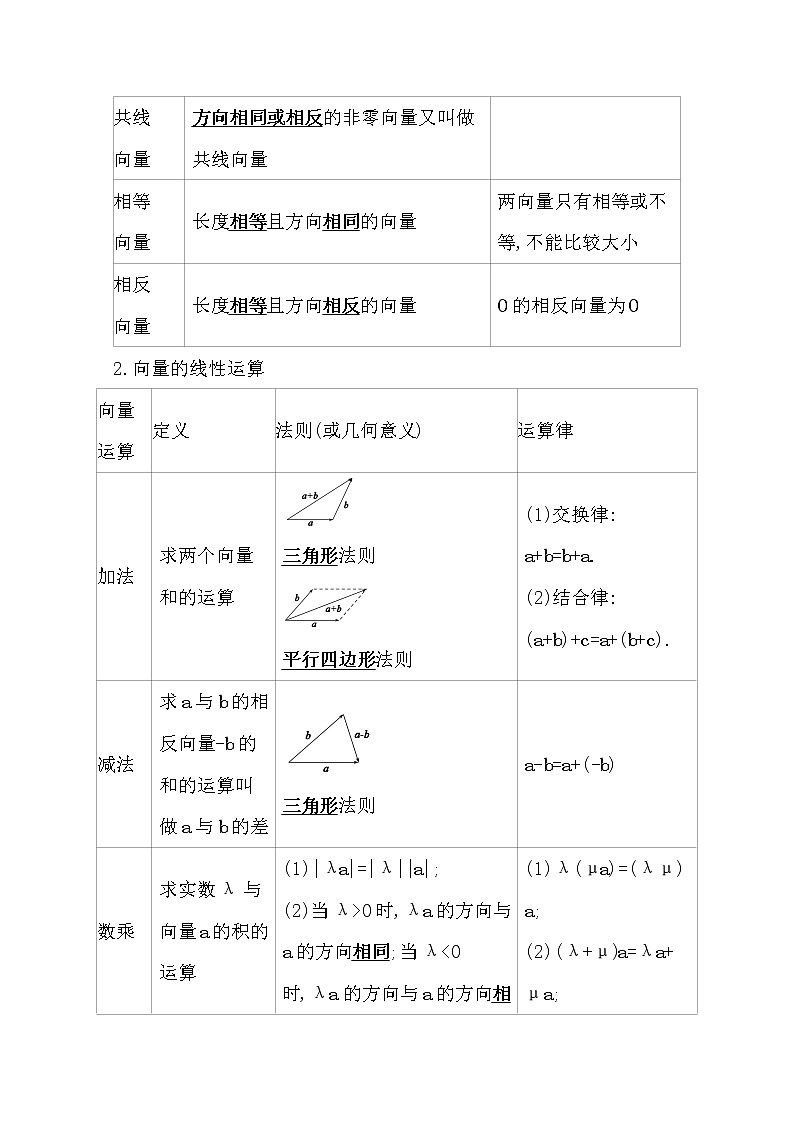
共线 向量 | 方向相同或相反的非零向量又叫做共线向量 | |
相等 向量 | 长度相等且方向相同的向量 | 两向量只有相等或不等,不能比较大小 |
相反 向量 | 长度相等且方向相反的向量 | 0的相反向量为0 |
2.向量的线性运算
向量 运算 | 定义 | 法则(或几何意义) | 运算律 |
加法 | 求两个向量和的运算 | 三角形法则 平行四边形法则 | (1)交换律: a+b=b+a. (2)结合律: (a+b)+c=a+(b+c). |
减法 | 求a与b的相反向量-b的和的运算叫做a与b的差 | 三角形法则 | a-b=a+(-b) |
数乘 | 求实数λ与向量a的积的运算 | (1)|λa|=|λ||a|; (2)当λ>0时,λa的方向与a的方向相同;当λ<0时,λa的方向与a的方向相反;当λ=0时,λa=0 | (1)λ(μa)=(λμ)a; (2)(λ+μ)a=λa+μa; (3)λ(a+b)=λa+λb |
3.共线向量定理
向量a(a≠0)与b共线,当且仅当有唯一一个实数λ,使b=λa.
1.易错点:解决向量的概念问题应关注以下五点
(1)共线向量即平行向量,它们均与起点无关.
(2)相等向量不仅模相等,而且方向要相同,所以相等向量一定是平行向量,而平行向量未必是相等向量.
(3)向量可以平移,平移后的向量与原向量是相等向量.解题时,不要把它与函数图象移动混为一谈.
(4)非零向量a与的关系:是a方向上的单位向量.
(5)向量与数量不同,数量可以比较大小,向量则不能,但向量的模是非负实数,故可以比较大小.
2.注意点:
(1)平面向量的线性运算
①进行向量运算时,要尽可能地将它们转化到三角形或平行四边形中,充分利用相等向量、相反向量,三角形的中位线及相似三角形对应边成比例等性质,把未知向量用已知向量表示出来.
②向量的线性运算类似于代数多项式的运算,实数运算中的去括号、移项、合并同类项、提取公因式等变形手段在线性运算中同样适用.
(2)共线向量定理的主要应用:
①证明向量共线:对于非零向量a,b,若存在实数λ,使a=λb,则a与b共线.
②证明三点共线:若存在实数λ,使=λ,则A,B,C三点共线.
③A,B,C三点共线,O为A,B,C所在直线外任意一点,则=λ+μ且λ+μ=1.
基础小题
1.给出下列说法:①零向量的长度为零,方向是任意的;②若a,b都是单位向量,则a=b;③向量与相等.则所有正确命题的序号是 ( )
A.① B.③ C.①③ D.①②
【解析】选A.根据零向量的定义可知①正确;根据单位向量的定义可知,单位向量的模相等,但方向不一定相同,故两个单位向量不一定相等,故②错误;向量与互为相反向量,故③错误.
2.设b是a的相反向量,则下列说法一定错误的是 ( )
A.a与b的长度相等 B.a∥b
C.a与b一定不相等 D.a是b的相反向量
【解析】选C.相反向量是长度相等,方向相反的两个向量,故选项A,B,D正确,选项C错误.
3.设D为△ABC所在平面内一点,=3,则 ( )
A.=-+ B.=-
C.=+ D.=-
【解析】选A.因为=3,
所以-=3(-),
即4-=3,所以=-+.
4.若四边形ABCD满足=,则四边形ABCD的形状是________.
【解析】=表示AD∥BC且AD=BC,
所以四边形ABCD是平行四边形.
答案:平行四边形
5.(教材改编)已知▱ABCD的对角线AC和BD相交于O,且=a,=b,则=________,=________(用a,b表示).
【解析】如图,==-=b-a,
=-=--=-a-b.
答案:b-a -a-b
6.已知a与b是两个不共线向量,且向量a+λb与-(b-3a)共线,则λ=________.
【解析】由已知得a+λb=-k(b-3a),
所以解得
答案:-
关闭Word文档返回原板块








