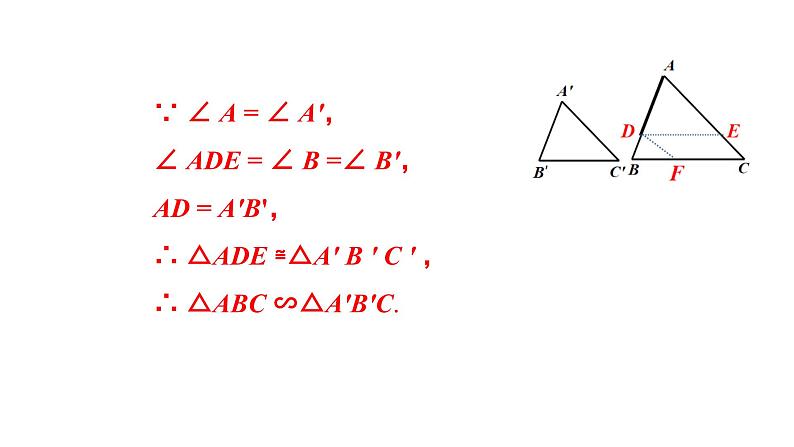
北师大版九年级上册5 相似三角形判定定理的证明教案配套ppt课件

这是一份北师大版九年级上册5 相似三角形判定定理的证明教案配套ppt课件，共15页。PPT课件主要包含了∴DECF，而∠BAC∠DAE，∴△ABC∽△ADE，∴DEB′C′，∴AEA′C′，选讲内容，∠ABE∠AEB，∠ABD∠C，∠B∠B等内容，欢迎下载使用。

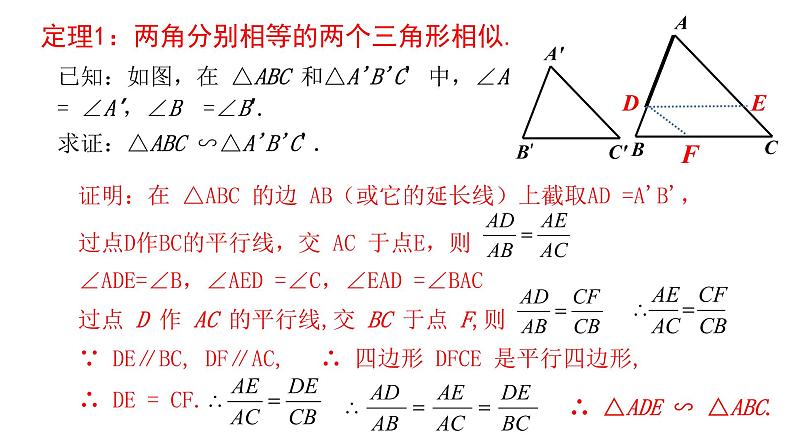
定理1：两角分别相等的两个三角形相似.
已知：如图，在 △ABC 和△A'B'C' 中，∠A = ∠A′，∠B =∠B′. 求证：△ABC ∽△A'B'C'．
证明：在 △ABC 的边 AB（或它的延长线）上截取AD =A'B'，过点D作BC的平行线，交 AC 于点E，则
∠ADE=∠B，∠AED =∠C，∠EAD =∠BAC
过点 D 作 AC 的平行线,交 BC 于点 F,则
∵ DE∥BC, DF∥AC,
∴ 四边形 DFCE 是平行四边形,
∴ △ADE ∽ △ABC.
∵ ∠ A = ∠ A'，∠ ADE = ∠ B =∠ B'，AD = A'B'，∴ △ADE ≌△A' B ' C ' ， ∴ △ABC ∽△A'B'C.
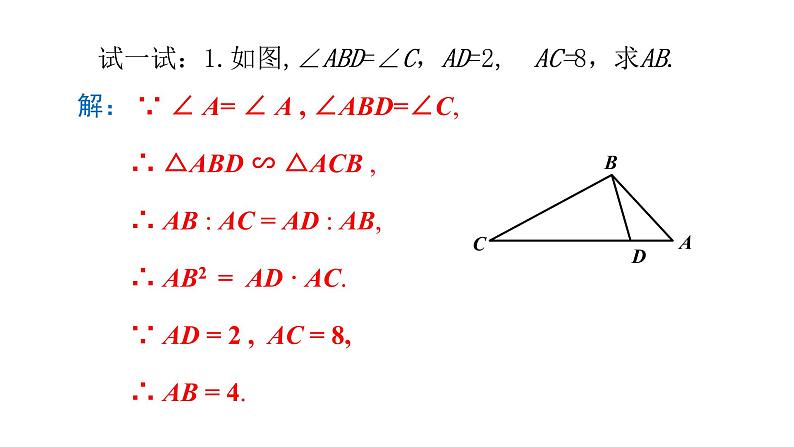
试一试：1.如图,∠ABD=∠C，AD=2, AC=8，求AB.
解： ∵ ∠ A= ∠ A , ∠ABD=∠C, ∴ △ABD ∽ △ACB , ∴ AB : AC = AD : AB, ∴ AB2 = AD · AC. ∵ AD = 2 , AC = 8, ∴ AB = 4.
定理2:两边成比例且夹角相等的两个三角形相似.
已知：如图，在△ABC 和△A′B′C′ 中，∠A =∠ A'， 求证：△ABC ∽ △A′B′C′.
证明：在△ABC 的边 AB（或它的延长线）上截取 AD = A′B′，过点 D 作 BC 的平行线，交 AC 于点 E，则
∴ △ABC ∽ △ADE，
∴ AE =A'C'.
∵ ∠ A=∠ A'，
∴ △ADE ≌ △A'B'C'，
∴ △ABC ∽ △A'B'C'.
2.如图，在四边形ABCD中，∠B=∠ACD，AB=6，BC=4，AC=5，CD= ，求AD的长.
解: ∵ AB=6，BC=4，AC=5，CD = 又∠B =∠ACD, ∴△ABC∽△DCA， ∴
定理3：三边成比例的两个三角形相似.
已知：如图，在 △ABC 和△A′B′C′ 中， 求证：△ABC ∽ △A′B′C′ .
证明：在△ABC的边AB,AC（或它们的延长线）上分别截取AD=A′B′,AE=A′C′,连接DE.
∴△ADE≌△A′B′C′
∴△ABC∽△A′B′C′
已知：如图，在 △ABC 和△A′B′C′ 中， 求证：△ABC ∽ △A′B′C′ .
△ABC ∽ △ADE
3.如图，在大小为4×4的正方形网格中，是相似三角形的是（ ）
提示：计算三边的长，算三边是否成比例
作业布置：习题2.5 1，2，3
1.已知：如图，在△ABC中，D是边AC上的一点，∠CBD的平分线交AC于点E,且AE=AB.求证：AE2=AD·AC.
即AB2=AD·AC.
提示：由AE=AB,得
而∠ABE=∠ABD+∠DBE,
∠AEB=∠C+∠EBC,
由∠DBE=∠EBC,得
于是△ABD∽△ACB,
由AE=AB,得AE2=AD·AC.
2.已知：如图S4-5-11，在△ABC中，点D，E分别在边AB，BC上，BA·BD=BC·BE（1）求证：DE·AB=AC·BE；（2）如果AC2=AD·AB，求证：AE=AC.
证明：（1）∵BA·BD=BC·BE，∴又∵∠B=∠B， ∴ .∴DE·AB=AC·BE.（2）∵AC2=AD·AB，∴ .∵∠DAC=∠CAB，∴△ADC∽△ACB.∴∠ACD=∠B.∵ ，∴△BAE∽△BCD.∵∠AEC=∠B+∠BAE，∠ACE=∠ACD+∠BCD，∴∠AEC=∠ACE.∴AE=AC.
∴△ABC∽△EBD.
∴∠BAE=∠BCD.
3.如图S4-5-12，在△ABC中，AD是BC边上的中线，点E,F在AB边上，连接DE，CF交AD于G，点E是BF中点．(1)求证：△AFG∽△AED;(2)若FG=2，G为AD中点，求CG的长．
(1)证明：∵AD是BC边上的中线，点E是BF中点，∴BD=CD，BE=EF.∴DE是△BCF的中位线.∴DE∥CF.∴DE∥FG.∴△AFG∽△AED.