



北师大版4 探索三角形相似的条件授课ppt课件
展开1、什么叫相似多边形? 各角分别相等,各边成比例的两个多边形叫做相似多边形。2、根据相似多边形的定义,什么叫相似三角形呢?
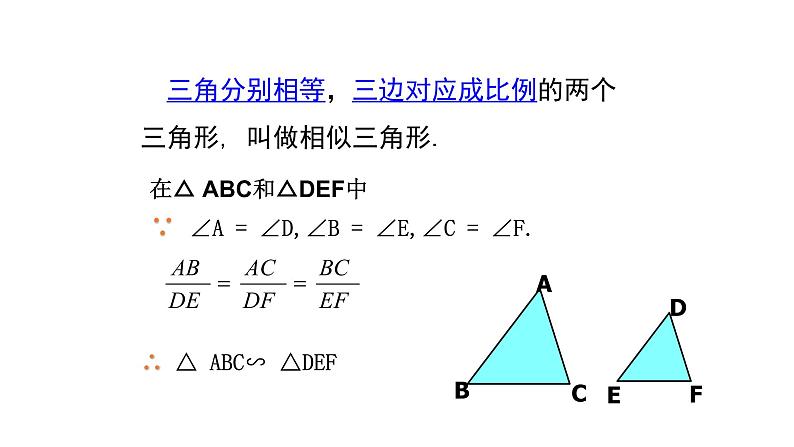
三角分别相等,三边对应成比例的两个三角形, 叫做相似三角形.
在△ ABC和△DEF中∵ ∠A = ∠D,∠B = ∠E,∠C = ∠F.
∴ △ ABC∽ △DEF
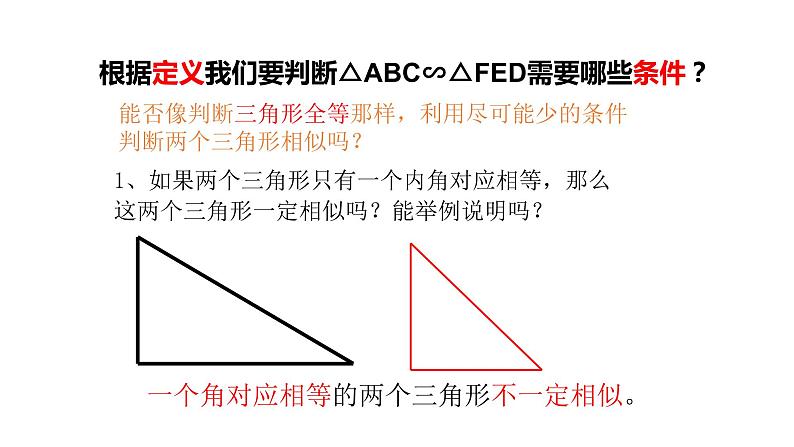
根据定义我们要判断△ABC∽△FED需要哪些条件?
能否像判断三角形全等那样,利用尽可能少的条件判断两个三角形相似吗?
1、如果两个三角形只有一个内角对应相等,那么这两个三角形一定相似吗?能举例说明吗?
一个角对应相等的两个三角形不一定相似。
2、如果两个三角形有两个内角对应相等,那么这两个三角形一定相似吗?
请依据下列条件画三角形:同桌两人一组, 一人画△ABC,另一人画△A′B′C′,使∠A= ∠A′=45 ° ,∠B= ∠B′=60 °。
① ∠C= ∠C′吗?
定理:两角对应相等的两个三角形相似
∠A= ∠A′∠B= ∠B′
∴△ABC∽△A′B′C′
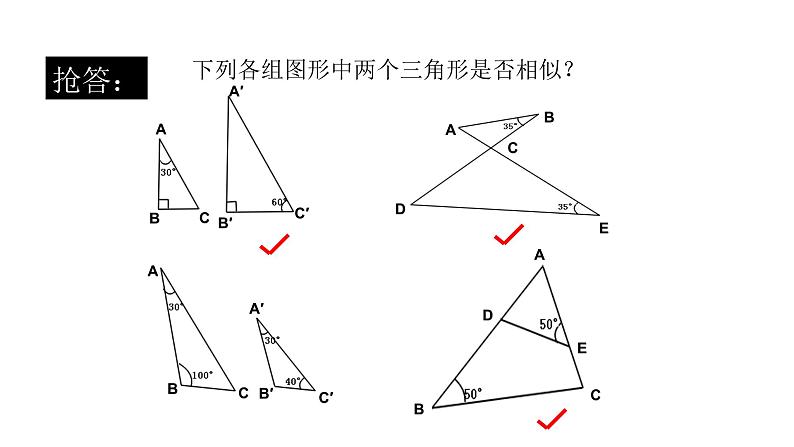
下列各组图形中两个三角形是否相似?
例:如图,D,E分别是△ ABC边AB,AC上的点, DE∥BC. (1)△ ADE 与 △ ABC 相似吗?为什么?(2)若AD=3,AB=7,DE=2,求BC的长。(3)AD ∙ AC=AE ∙ AB吗?试说明理由。
解:(1)∵DE∥BC
∴△ ADE ~ △ ABC
(3)∵△ ADE ~ △ ABC
∴AD ∙ AC=AE ∙ AB
提高训练.如图,已知点D,E分别在AB,AC或它们的延长线上,且∠1=∠2,分别指出图中的相似三角形。
作业布置:习题4.5 1,2,3,4,5
1.如图,△ABC是等边三角形,CE是外角平分线,点D在AC上,连接BD并延长与CE交于点E,求证:△ABD∽△CED
2.已知:如图,在Rt△ABC中,∠ACB=90° CD⊥AB于D,想一想,图中有哪两个三角 形相似?
有三对相似三角形,它们是△ADC∽△CDB,△ADC∽△ACB,△CDB∽△ACB,
是两个全等的等腰直角三角形,
北师大版九年级上册4 探索三角形相似的条件示范课课件ppt: 这是一份北师大版九年级上册4 探索三角形相似的条件示范课课件ppt,共20页。PPT课件主要包含了学习目标,复习回顾,相似多边形,相似三角形,类比全等三角形,全等三角形,那这样变化一下呢,对应角,对应边,全等是一种特殊的相似等内容,欢迎下载使用。
初中数学北师大版九年级上册4 探索三角形相似的条件优秀课件ppt: 这是一份初中数学北师大版九年级上册4 探索三角形相似的条件优秀课件ppt,文件包含核心素养目标441《探索三角形相似的条件》课件pptx、核心素养目标441《探索三角形相似的条件》教案docx等2份课件配套教学资源,其中PPT共20页, 欢迎下载使用。
初中北师大版第四章 图形的相似4 探索三角形相似的条件完整版ppt课件: 这是一份初中北师大版第四章 图形的相似4 探索三角形相似的条件完整版ppt课件,共23页。PPT课件主要包含了学习目标,全等三角形,讲授新课,那这样变化一下呢,相似三角形,对应角,对应边,全等是一种特殊的相似,角边角,ASA等内容,欢迎下载使用。













