

2020版高考数学一轮复习课后限时集训37《空间几何体的结构及其三视图和直观图》文数(含解析)北师大版 试卷
展开课后限时集训(三十七)
(建议用时:60分钟)
A组 基础达标
一、选择题
1.下列说法正确的是( )
A.有两个平面互相平行,其余各面都是平行四边形的多面体是棱柱
B.四棱锥的四个侧面都可以是直角三角形
C.有两个平面互相平行,其余各面都是梯形的多面体是棱台
D.棱台的各侧棱延长后不一定交于一点
B [如图①所示,可知A错.如图②,当PD⊥底面ABCD,且四边形ABCD为矩形时,则四个侧面均为直角三角形,B正确.
图 ① 图②
根据棱台的定义,可知C,D不正确.]
2.一个锥体的主视图和左视图如图所示,下面选项中,不可能是该锥体的俯视图的是 ( )
C [A,B,D选项满足三视图作法规则,C不满足三视图作法规则中的宽相等,故C不可能是该锥体的俯视图.]
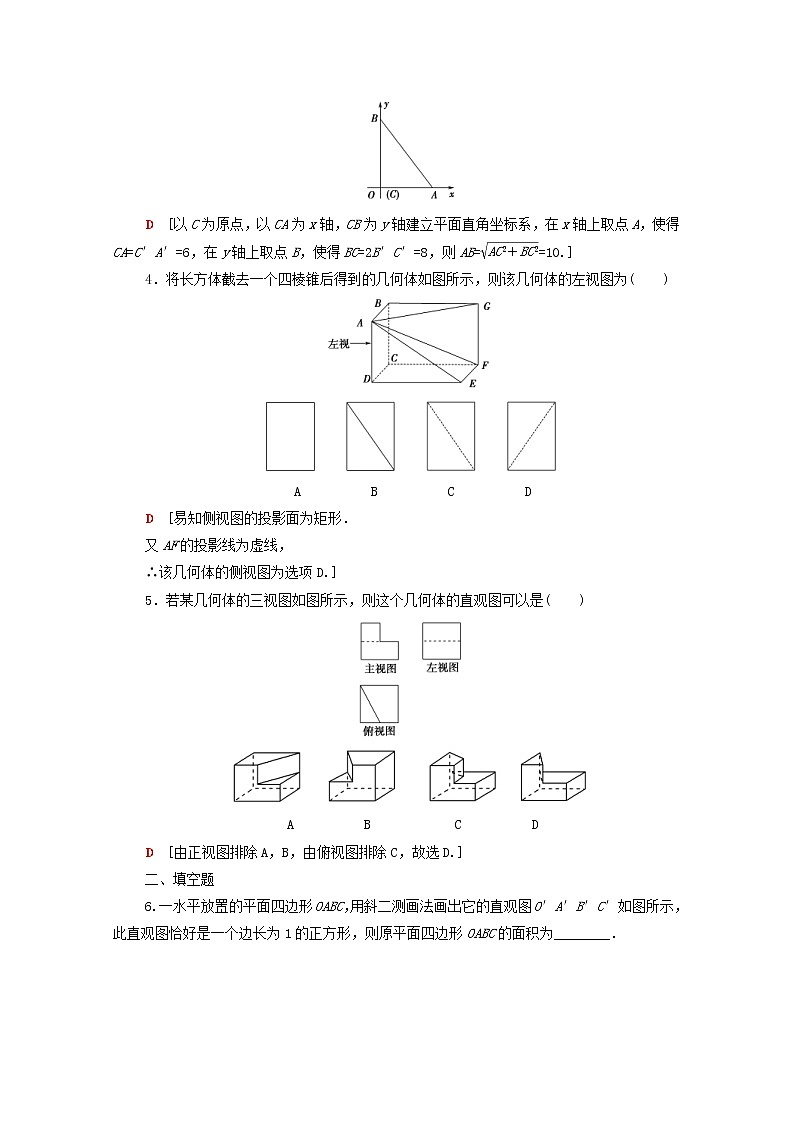
3.(2018·南昌模拟)如图,水平放置的△ABC的斜二测直观图是图中的△A′B′C′,已知A′C′=6,B′C′=4,则AB边的实际长度是( )
A.4 B.6
C.8 D.10
D [以C为原点,以CA为x轴,CB为y轴建立平面直角坐标系,在x轴上取点A,使得CA=C′A′=6,在y轴上取点B,使得BC=2B′C′=8,则AB==10.]
4.将长方体截去一个四棱锥后得到的几何体如图所示,则该几何体的左视图为( )
A B C D
D [易知侧视图的投影面为矩形.
又AF的投影线为虚线,
∴该几何体的侧视图为选项D.]
5.若某几何体的三视图如图所示,则这个几何体的直观图可以是( )
A B C D
D [由正视图排除A,B,由俯视图排除C,故选D.]
二、填空题
6.一水平放置的平面四边形OABC,用斜二测画法画出它的直观图O′A′B′C′如图所示,此直观图恰好是一个边长为1的正方形,则原平面四边形OABC的面积为________.
2 [因为直观图的面积是原图形面积的倍,且直观图的面积为1,所以原图形的面积为2.]
7.一个圆台上、下底面的半径分别为3 cm和8 cm,若两底面圆心的连线长为12 cm,则这个圆台的母线长为________cm.
13 [如图,过点A作AC⊥OB,交OB于点C.
在Rt△ACB中,AC=12 cm,BC=8-3=5(cm).
所以AB==13(cm).]
8.(2018·合肥模拟)已知某组合体的主视图与左视图相同,如图所示,其中AB=AC,四边形BCDE为矩形,则该组合体的俯视图可以是________.(填正确的序号)
①②③④ [由组合体的主视图与左视图可知,该组合体可以是正四棱柱与正四棱锥的组合体,则该组合体的俯视图为①;
该组合体可以是圆柱与正四棱锥的组合体,则该组合体的俯视图为②;
该组合体可以是圆柱与圆锥的组合体,则该组合体的俯视图为③;
该组合体可以是正四棱柱与圆锥的组合体,则该组合体的俯视图为④.]
三、解答题
9.某几何体的三视图如图所示.
(1)判断该几何体是什么几何体?
(2)画出该几何体的直观图.
[解] (1)该几何体是一个正方体切掉两个圆柱后的几何体.
(2)直观图如图所示.
图1
10.如图1,在四棱锥PABCD中,底面为正方形,PC与底面ABCD垂直,如图2为该四棱锥的主视图和左视图,它们是腰长为6 cm的全等的等腰直角三角形.
图2
(1)根据图中所给的主视图、左视图,画出相应的俯视图,并求出该俯视图的面积;
俯视图
(2)求PA.
[解] (1)该四棱锥的俯视图为(内含对角线)边长为6 cm的正方形,如图,其面积为36 cm2.
(2)由左视图可求得PD===6.
由主视图可知AD=6,且AD⊥PD,所以在Rt△APD中,PA==
=6 cm.
B组 能力提升
1.(2017·北京高考)某四棱锥的三视图如图所示,则该四棱锥的最长棱的长度为( )
A.3 B.2 C.2 D.2
B [在正方体中还原该四棱锥,如图所示,
可知SD为该四棱锥的最长棱.
由三视图可知正方体的棱长为2,
故SD==2.
故选B.]
2.(2019·泰安模拟)将一个长方体沿相邻三个面的对角线截去一个棱锥,得到的几何体的主视图与俯视图如图所示,则该几何体的左视图为( )
B [由几何体的主视图和俯视图可知该几何体为图①,
故其侧视图为图②.]
3.三棱锥SABC及其三视图中的主视图和左视图如图所示,则棱SB的长为________.
4 [由已知中的三视图可得SC⊥平面ABC,
且底面△ABC为等腰三角形,在△ABC中AC=4,AC边上的高为2,
故BC=4,在Rt△SBC中,由SC=4,可得SB=4.]
4.如图,一立在水平地面上的圆锥形物体的母线长为4 m,一只小虫从圆锥的底面圆上的点P出发,绕圆锥表面爬行一周后回到点P处.若该小虫爬行的最短路程为4 m,则圆锥底面圆的半径等于________m.
[把圆锥侧面沿过点P的母线展开成如图所示的扇形,
由题意OP=4,PP′=4,
则cos∠POP′
=
=-,
所以∠POP′=.
设底面圆的半径为r,
则2πr=×4,所以r=.]









