2020版高考数学一轮复习课后限时集训41《简单几何体的表面积与体积》文数（含解析）北师大版 试卷

课后限时集训(四十一)　

(建议用时：60分钟)

A组　基础达标

一、选择题

1．已知等腰直角三角形的直角边的长为2，将该三角形绕其斜边所在的直线旋转一周而形成的曲面所围成的几何体的体积为(　　)

A．　　　 B.

C．2π D．4π

B　[依题意知，该几何体是以为底面半径，为高的两个同底圆锥组成的组合体，则其体积V=π×()2×2=π.]

2．一个正方体挖去一个多面体所得的几何体的三视图如图所示，其中主视图、左视图和俯视图均为边长等于2的正方形，则这个几何体的表面积为(　　)

A．16＋4 B．16＋4

C．20＋4 D．20＋4

D　[由三视图可知，该几何体是棱长为2的正方体的内部挖去一个底面边长为2的正四棱锥，将三视图还原可得如图，

可得其表面积为S=5×22＋4××2×=20＋4，故选D.]

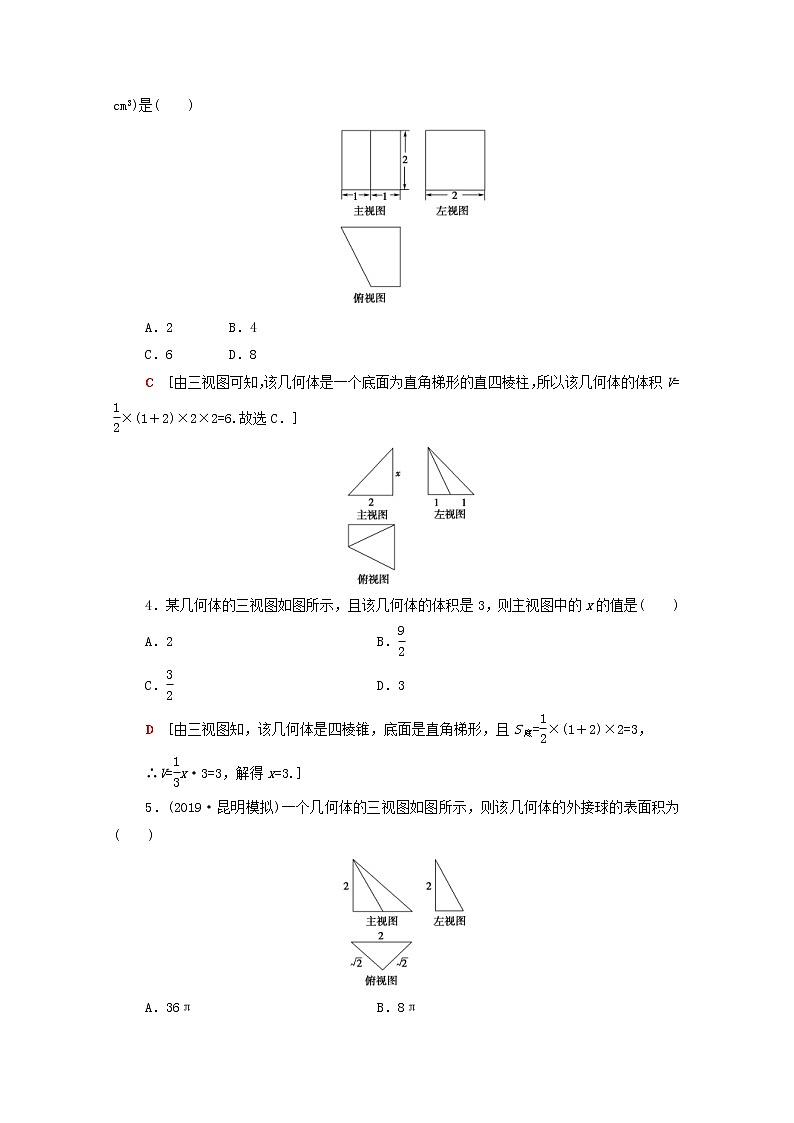
3．(2018·浙江高考)某几何体的三视图如图所示(单位：cm)，则该几何体的体积(单位：cm3)是(　　)

A．2　　　　B．4

C．6　　　　D．8

C　[由三视图可知，该几何体是一个底面为直角梯形的直四棱柱，所以该几何体的体积V=×(1＋2)×2×2=6.故选C．]

4．某几何体的三视图如图所示，且该几何体的体积是3，则主视图中的x的值是(　　)

A．2 B．

C． D．3

D　[由三视图知，该几何体是四棱锥，底面是直角梯形，且S底=×(1＋2)×2=3，

∴V=x·3=3，解得x=3.]

5．(2019·昆明模拟)一个几何体的三视图如图所示，则该几何体的外接球的表面积为(　　)

A．36π B．8π

C．π D．π

B　[根据几何体的三视图，得该几何体是底面为等腰直角三角形，高为2的直三棱锥，如图所示，

则该直三棱锥的外接球是对应直三棱柱的外接球，设几何体外接球的半径为R，∴2R=VB.

∵VB==2，∴R=，

∴该几何体的外接球的表面积是4πR2=8π.故选B.]

二、填空题

6．现有橡皮泥制作的底面半径为5，高为4的圆锥和底面半径为2，高为8的圆柱各一个，若将它们重新制作成总体积与高均保持不变，但底面半径相同的新的圆锥和圆柱各一个，则新的底面半径为______．

　[设新的底面半径为r，由题意得

×π×52×4＋π×22×8=×π×r2×4＋π×r2×8，

∴r2=7，∴r=.]

7．一个六棱锥的体积为2，其底面是边长为2的正六边形，侧棱长都相等，则该六棱锥的侧面积为________．

12　[设正六棱锥的高为h，棱锥的斜高为h′.

由题意，得×6××2××h=2，

∴h=1，∴斜高h′==2，

∴S侧=6××2×2=12.]

8．(2019·惠州模拟)已知三棱锥S­ABC，△ABC是直角三角形，其斜边AB=8，SC⊥平面ABC，SC=6，则三棱锥S­ABC的外接球的表面积为________．

100π　[将三棱锥S­ABC放在长方体中(图略)，易知三棱锥S­ABC所在长方体的外接球，即为三棱锥S­ABC的外接球，所以三棱锥S­ABC的外接球的直径2R==10，即三棱锥S ­ABC的外接球的半径R=5，所以三棱锥S­ABC的外接球的表面积S=4πR2=100π.]

三、解答题

9．如图，从正方体ABCD­A1B1C1D1的8个顶点中选出的4个点恰为一个正四面体的顶点．

(1)若选出4个顶点包含点A，请在图中画出这个正四面体；

(2)求棱长为a的正四面体外接球的半径．

[解]　(1)如图所示，选取的四个点分别为A，D1，B1，C．

(2)棱长为a的正四面体外接球的半径等于正方体外接球的半径等于正方体对角线长的一半，因为正四面体的棱长a，所以正方体的边长为a，因此外接球的半径为×a=a.

10．(2015·全国卷Ⅱ)如图，长方体ABCD­A1B1C1D1中，AB=16，BC=10，AA1=8，点E，F分别在A1B1，D1C1上，A1E=D1F=4.过点E，F的平面α与此长方体的面相交，交线围成一个正方形．

(1)在图中画出这个正方形(不必说明画法和理由)；

(2)求平面α把该长方体分成的两部分体积的比值．

[解]　(1)交线围成的正方形EHGF如图所示．

(2)如图，作EM⊥AB，垂足为M，则AM=A1E=4，EB1=12，EM=AA1=8.

因为四边形EHGF为正方形，所以EH=EF=BC=10.

于是MH==6，AH=10，HB=6.

故S四边形A1EHA=×(4＋10)×8=56，

S四边形EB1BH=×(12＋6)×8=72.

因为长方体被平面α分成两个高为10的直棱柱，

所以其体积的比值为.

B组　能力提升

1．(2019·青岛模拟)如图为某个几何体的三视图，则该几何体的体积为(　　)

A．12－　　　　　B．12－π

C．12－ D．12－

A　[由三视图可知，该几何体是由一个正四棱柱挖掉一个半圆锥所得到的几何体，其直观图如图所示，其中正四棱柱的底面正方形的边长a=2，半圆锥的底面半径r=1，高h=3，所以正四棱柱的体积V1=a2h=22×3=12，半圆锥的体积V2=×r2h=×12×3=，所以该几何体的体积V=V1－V2=12－.]

2．(2018·株洲模拟)已知正三棱锥P­ABC的主视图和俯视图如图所示，则此三棱锥外接球的表面积为(　　)

A． B．

C． D．12π

B　[如图，作PG⊥CB于点G，连接AG，设点P在底面ABC内的射影为D，连接PD，依题易得AB=2，PG=，PA=4，AD=2，PD=2，PD⊥平面ABC．易知，正三棱锥P­ABC外接球的球心在PD上，不妨设球心为O，半径为r，连接OA，则在Rt△AOD中，r2=22＋(2－r)2⇒r2=，S=4πr2=.故选B.]

3．(2018·全国卷Ⅱ)已知圆锥的顶点为S，母线SA，SB互相垂直，SA与圆锥底面所成角为30°.若△SAB的面积为8，则该圆锥的体积为________．

8π　[由题意画出图形，如图，设AC是底面圆O的直径，连接SO，则SO是圆锥的高．设圆锥的母线长为l，则由SA⊥SB，△SAB的面积为8，得l2=8，得l=4.在Rt△ASO中，由题意知∠SAO=30°，所以SO=l=2，AO=l=2.故该圆锥的体积V=π×AO2×SO=π×(2)2×2=8π.]

4．一个透明的球形装饰品内放置了两个公共底面的圆锥，且这两个圆锥的顶点和底面圆周都在这个球面上，如图，已知圆锥底面面积是这个球面面积的，设球的半径为R，圆锥底面半径为r.

(1)试确定R与r的关系，并求出较大圆锥与较小圆锥的体积之比；

(2)求出两个圆锥的体积之和与球的体积之比．

[解]　(1)不妨设球的半径为4；

则球的表面积为64π，圆锥的底面积为12π，

所以圆锥的底面半径为2.

由几何体的特征知球心到圆锥底面的距离，球的半径以及圆锥底面的半径三者可以构成一个直角三角形．

由此可以求得球心到圆锥底面的距离是=2，

所以圆锥体积较小者的高为4－2=2，

同理可得圆锥体积较大者的高为4＋2=6.

又由这两个圆锥的底面相同，

所以较大圆锥与较小圆锥的体积之比等于它们高之比，即3∶1.

(2)由(1)可得两个圆锥的体积和为·π·(2)2·8=32π，球的体积为·π·43=π，

故两个圆锥的体积之和与球的体积之比为32π∶π=3∶8.