
人教A版 (2019)必修 第一册5.5 三角恒等变换第1课时导学案及答案
展开5.5 三角恒等变换
5.5.1 两角和与差的正弦、余弦和正切公式
第1课时 两角差的余弦公式
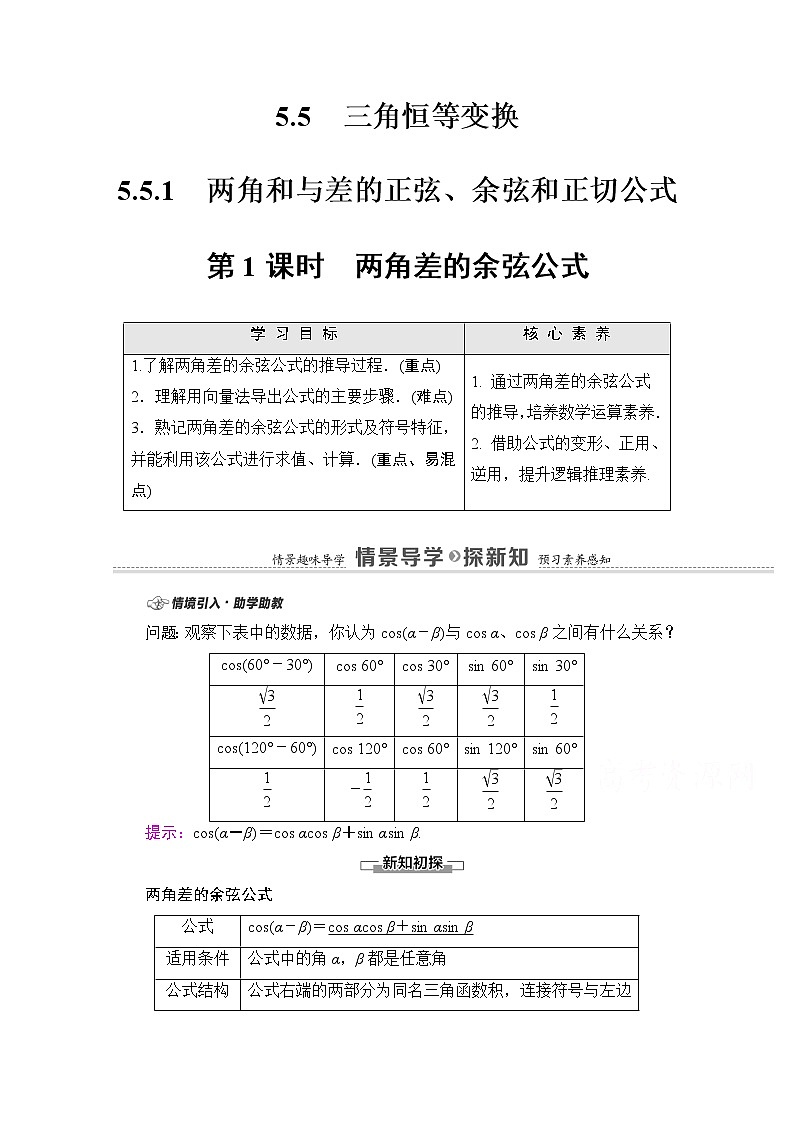
问题:观察下表中的数据,你认为cs(α-β)与cs α、cs β之间有什么关系?
提示:cs(α-β)=cs αcs β+sin αsin β.
两角差的余弦公式
1.思考辨析(正确的画“√”,错误的画“×”)
(1)cs(60°-30°)=cs 60°-cs 30°.( )
(2)对于任意实数α,β,cs(α-β)=cs α-cs β都不成立.
( )
(3)对任意α,β∈R,cs(α-β)=cs αcs β+sin αsin β都成立.
( )
(4)cs 30°cs 120°+sin 30°sin 120°=0.( )
[提示] (1)错误.cs(60°-30°)=cs 30°≠cs 60°-cs 30°.
(2)错误.当α=-45°,β=45°时,cs(α-β)=cs(-45°-45°)=cs(-90°)=0,cs α-cs β=cs(-45°)-cs 45°=0,此时cs(α-β)=cs α-cs β.
(3)正确.结论为两角差的余弦公式.
(4)正确.cs 30°cs 120°+sin 30°sin 120°=cs(120°-30°)=cs 90°=0.
[答案] (1)× (2)× (3)√ (4)√
2.sin 14°cs 16°+sin 76°cs 74°=( )
A.eq \f(\r(3),2) B.eq \f(1,2)
C.-eq \f(\r(3),2) D.-eq \f(1,2)
B [∵sin 14°=cs 76°,cs 74°=sin 16°,
∴原式=cs 76°cs 16°+sin 76°sin 16°=cs(76°-16°)=cs 60°=eq \f(1,2).]
3.cs(-15°)的值是( )
A.eq \f(\r(6)-\r(2),2) B.eq \f(\r(6)+\r(2),2)
C.eq \f(\r(6)-\r(2),4) D.eq \f(\r(6)+\r(2),4)
D [cs(-15°)=cs 15°=cs(45°-30°)=cs 45°cs 30°+sin 45°sin 30°=eq \f(\r(2),2)×eq \f(\r(3),2)+eq \f(\r(2),2)×eq \f(1,2)=eq \f(\r(6)+\r(2),4).]
4.cs 65°cs 20°+sin 65°sin 20°= .
eq \f(\r(2),2) [cs 65°cs 20°+sin 65°sin 20°=cs(65°-20°)=cs 45°=eq \f(\r(2),2).]
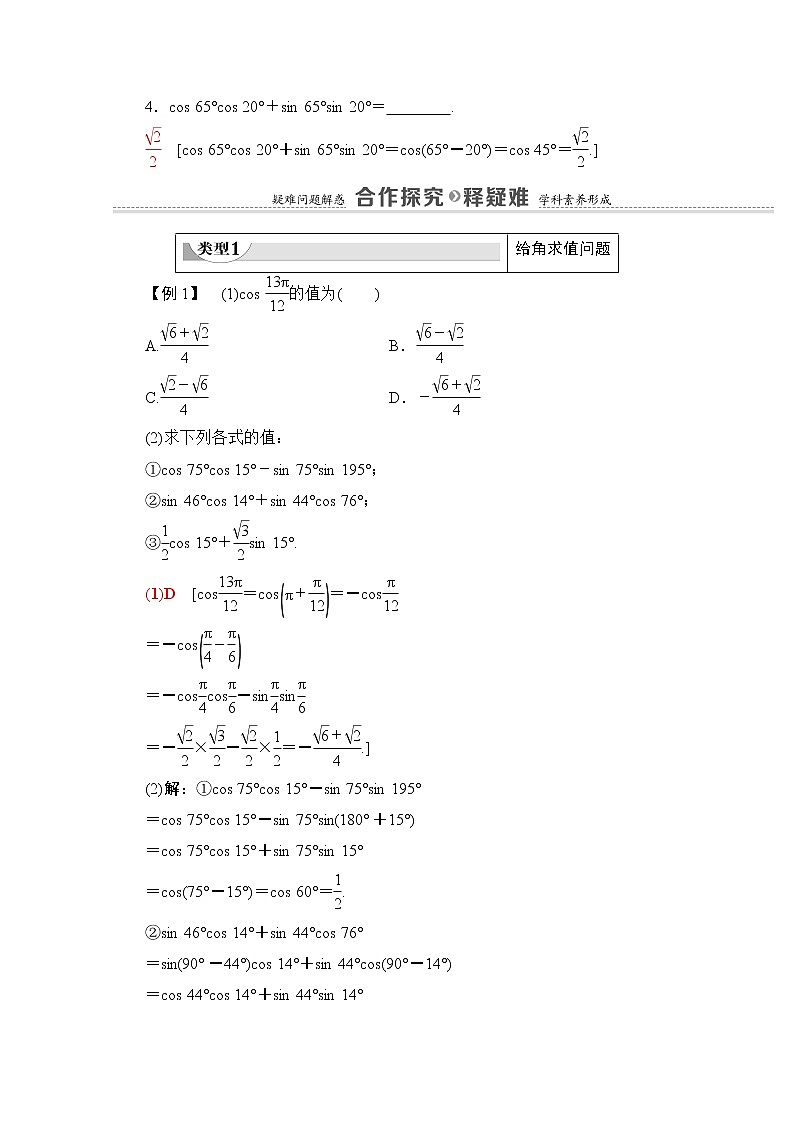
【例1】 (1)cseq \f(13π,12)的值为( )
A.eq \f(\r(6)+\r(2),4) B.eq \f(\r(6)-\r(2),4)
C.eq \f(\r(2)-\r(6),4) D.-eq \f(\r(6)+\r(2),4)
(2)求下列各式的值:
①cs 75°cs 15°-sin 75°sin 195°;
②sin 46°cs 14°+sin 44°cs 76°;
③eq \f(1,2)cs 15°+eq \f(\r(3),2)sin 15°.
(1)D [cseq \f(13π,12)=cseq \b\lc\(\rc\)(\a\vs4\al\c1(π+\f(π,12)))=-cseq \f(π,12)
=-cseq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,4)-\f(π,6)))
=-cseq \f(π,4)cseq \f(π,6)-sineq \f(π,4)sineq \f(π,6)
=-eq \f(\r(2),2)×eq \f(\r(3),2)-eq \f(\r(2),2)×eq \f(1,2)=-eq \f(\r(6)+\r(2),4).]
(2)解:①cs 75°cs 15°-sin 75°sin 195°
=cs 75°cs 15°-sin 75°sin(180°+15°)
=cs 75°cs 15°+sin 75°sin 15°
=cs(75°-15°)=cs 60°=eq \f(1,2).
②sin 46°cs 14°+sin 44°cs 76°
=sin(90°-44°)cs 14°+sin 44°cs(90°-14°)
=cs 44°cs 14°+sin 44°sin 14°
=cs(44°-14°)=cs 30°=eq \f(\r(3),2).
③eq \f(1,2)cs 15°+eq \f(\r(3),2)sin 15°
=cs 60°cs 15°+sin 60°sin 15°
=cs(60°-15°)=cs 45°
=eq \f(\r(2),2).
1.解含非特殊角的三角函数式的求值问题的一般思路是:
(1)把非特殊角转化为特殊角的和或差,正用公式直接求值.
(2)在转化过程中,充分利用诱导公式,构造两角差的余弦公式的结构形式,然后逆用公式求值.
2.两角差的余弦公式的结构特点:
(1)同名函数相乘:即两角余弦乘余弦,正弦乘正弦.
(2)把所得的积相加.
eq \([跟进训练])
1.化简下列各式:
(1)cs(θ+21°)cs(θ-24°)+sin(θ+21°)sin(θ-24°);
(2)-sin 167°·sin 223°+sin 257°·sin 313°.
[解] (1)原式=cs[θ+21°-(θ-24°)]=cs 45°=eq \f(\r(2),2).
(2)原式=-sin(180°-13°)sin(180°+43°)+sin(180°+77°)·sin(360°-47°)
=sin 13°sin 43°+sin 77°sin 47°
=sin 13°sin 43°+cs 13°cs 43°
=cs(13°-43°)=cs(-30°)=eq \f(\r(3),2).
[探究问题]
1.若已知α+β和β的三角函数值,如何求cs α的值?
提示:cs α=cs[(α+β)-β]
=cs(α+β)cs β+sin(α+β)sin β.
2.利用α-(α-β)=β可得cs β等于什么?
提示:cs β=cs[α-(α-β)]
=cs αcs(α-β)+sin αsin(α-β).
【例2】 (1)已知sin α-sin β=1-eq \f(\r(3),2),cs α-cs β=eq \f(1,2),则cs(α-β)=( )
A.-eq \f(\r(3),2) B.-eq \f(1,2)
C.eq \f(1,2) D.eq \f(\r(3),2)
(2)已知sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,3)+α))=eq \f(12,13),α∈eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,6),\f(2π,3))),求cs α的值.
[思路点拨] (1)先将已知两式平方,再将所得两式相加,结合平方关系和公式C(α-β)求cs(α-β).
(2)由已知角eq \f(π,3)+α与所求角α的关系即α=eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,3)+α))-eq \f(π,3)寻找解题思路.
(1)D [因为sin α-sin β=1-eq \f(\r(3),2),
所以sin2α-2sin αsin β+sin2β=eq \b\lc\(\rc\)(\a\vs4\al\c1(1-\f(\r(3),2)))eq \s\up12(2), ①
因为cs α-cs β=eq \f(1,2),所以cs2α-2cs αcs β+cs2β=eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)))eq \s\up12(2), ②
①,②两式相加得1-2cs(α-β)+1=1-eq \r(3)+eq \f(3,4)+eq \f(1,4)
所以-2cs(α-β)=-eq \r(3)
所以cs(α-β)=eq \f(\r(3),2).
(2)[解] ∵α∈eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,6),\f(2π,3))),∴eq \f(π,3)+α∈eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2),π)),
∴cseq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,3)+α))=-eq \r(1-sin2\b\lc\(\rc\)(\a\vs4\al\c1(\f(π,3)+α)))
=-eq \r(1-\b\lc\(\rc\)(\a\vs4\al\c1(\f(12,13)))eq \s\up12(2))=-eq \f(5,13).
∵α=eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,3)+α))-eq \f(π,3),
∴cs α=cseq \b\lc\[\rc\](\a\vs4\al\c1(\b\lc\(\rc\)(\a\vs4\al\c1(\f(π,3)+α))-\f(π,3)))
=cseq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,3)+α))cseq \f(π,3)+sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,3)+α))sineq \f(π,3)=-eq \f(5,13)×eq \f(1,2)+eq \f(12,13)×eq \f(\r(3),2)=eq \f(12\r(3)-5,26).]
1.将例2(2)的条件改为“sineq \b\lc\(\rc\)(\a\vs4\al\c1(α+\f(π,4)))=eq \f(4,5),且eq \f(π,4)<α
[解] ∵sineq \b\lc\(\rc\)(\a\vs4\al\c1(α+\f(π,4)))=eq \f(4,5),且eq \f(π,4)<α
∴eq \f(π,2)<α+eq \f(π,4)<π,
∴cseq \b\lc\(\rc\)(\a\vs4\al\c1(α+\f(π,4)))=-eq \r(1-\b\lc\(\rc\)(\a\vs4\al\c1(\f(4,5)))eq \s\up12(2))=-eq \f(3,5),
∴cs α=cseq \b\lc\[\rc\](\a\vs4\al\c1(\b\lc\(\rc\)(\a\vs4\al\c1(α+\f(π,4)))-\f(π,4)))
=cseq \b\lc\(\rc\)(\a\vs4\al\c1(α+\f(π,4)))cs eq \f(π,4)+sineq \b\lc\(\rc\)(\a\vs4\al\c1(α+\f(π,4)))sin eq \f(π,4)
=-eq \f(3,5)×eq \f(\r(2),2)+eq \f(4,5)×eq \f(\r(2),2)=eq \f(\r(2),10).
2.将例2(2)的条件改为“sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,3)-α))=-eq \f(12,13),α∈eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,6),\f(5π,6)))”,求cseq \b\lc\(\rc\)(\a\vs4\al\c1(α-\f(π,12)))的值.
[解] ∵eq \f(π,6)<α<eq \f(5π,6),∴-eq \f(π,2)<eq \f(π,3)-α<eq \f(π,6),
又sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,3)-α))=-eq \f(12,13)<0,
∴-eq \f(π,2)<eq \f(π,3)-α<0,cseq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,3)-α))=eq \r(1-sin2\b\lc\(\rc\)(\a\vs4\al\c1(\f(π,3)-α)))=eq \f(5,13),
∴cseq \b\lc\(\rc\)(\a\vs4\al\c1(α-\f(π,12)))=cseq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,12)-α))
=cseq \b\lc\[\rc\](\a\vs4\al\c1(\b\lc\(\rc\)(\a\vs4\al\c1(\f(π,3)-α))-\f(π,4)))
=eq \f(\r(2),2)cseq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,3)-α))+eq \f(\r(2),2)sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,3)-α))
=eq \f(\r(2),2)×eq \f(5,13)+eq \f(\r(2),2)×eq \b\lc\(\rc\)(\a\vs4\al\c1(-\f(12,13)))=-eq \f(7\r(2),26).
给值求值问题的解题策略
(1)已知某些角的三角函数值,求另外一些角的三角函数值时,要注意观察已知角与所求表达式中角的关系,即拆角与凑角.
(2)由于和、差角与单角是相对的,因此解题过程中可以根据需要灵活地进行拆角或凑角.常见角的变换有:
①α=(α-β)+β;
②α=eq \f(α+β,2)+eq \f(α-β,2);
③2α=(α+β)+(α-β);
④2β=(α+β)-(α-β).
【例3】 已知sin(π-α)=eq \f(4\r(3),7),cs(α-β)=eq \f(13,14),0<β<α<eq \f(π,2),求角β的大小.
[思路点拨] eq \x(求cs α、sinα-β)→→eq \x(求β)
[解] 因为sin(π-α)=eq \f(4\r(3),7),
所以sin α=eq \f(4\r(3),7).因为0<α<eq \f(π,2),
所以cs α=eq \r(1-sin2α)=eq \f(1,7).
因为cs(α-β)=eq \f(13,14),
且0<β<α<eq \f(π,2),所以0<α-β<eq \f(π,2),
所以sin(α-β)=eq \r(1-cs2α-β)=eq \f(3\r(3),14),
所以cs β=cs[α-(α-β)]=cs αcs(α-β)+sin αsin(α-β)=eq \f(1,7)×eq \f(13,14)+eq \f(4\r(3),7)×eq \f(3\r(3),14)=eq \f(1,2).因为0<β<eq \f(π,2),所以β=eq \f(π,3).
已知三角函数值求角的解题步骤
1界定角的范围,根据条件确定所求角的范围.
2求所求角的某种三角函数值.为防止增解最好选取在范围内单调的三角函数.
3结合三角函数值及角的范围求角.
提醒:在根据三角函数值求角时,易忽视角的范围,而得到错误答案.
eq \([跟进训练])
2.已知α,β均为锐角,且cs α=eq \f(2\r(5),5),cs β=eq \f(\r(10),10),求α-β的值.
[解] ∵α,β均为锐角,
∴sin α=eq \f(\r(5),5),sin β=eq \f(3\r(10),10),
∴cs(α-β)=cs αcs β+sin αsin β
=eq \f(2\r(5),5)×eq \f(\r(10),10)+eq \f(\r(5),5)×eq \f(3\r(10),10)=eq \f(\r(2),2).
又sin α
∴0<α<β
故α-β=-eq \f(π,4).
1.记牢1个公式
cs(α-β)=cs αcs β+sinαsin β
2.掌握2类问题——求值、求角
(1)给式求值或给值求值问题,即由给出的某些函数关系式或某些角的三角函数值,求另外一些角的三角函数值,关键在于“变式”或“变角”,使“目标角”换成“已知角”.注意公式的正用、逆用、变形用,有时需运用拆角、拼角等技巧.
(2)“给值求角”问题,实际上也可转化为“给值求值”问题,求一个角的值,可分以下三步进行:①求角的某一三角函数值;②确定角所在的范围(找一个单调区间);③确定角的值.确定用所求角的哪种三角函数值,要根据具体题目而定.
3.规避1个易错
求角时易忽视角的范围.
1.sin 11°cs 19°+cs 11°cs 71°的值为( )
A.eq \f(\r(3),2) B.eq \f(1,2)
C.eq \f(1+\r(3),2) D.eq \f(\r(3)-1,2)
B [sin 11°cs 19°+cs 11°cs 71°=cs 11°·cs 71°+sin 11°sin 71°=cs(11°-71°)=cs(-60°)=eq \f(1,2).故选B.]
2.已知α为锐角,β为第三象限角,且cs α=eq \f(12,13),sin β=-eq \f(3,5),则cs(α-β)的值为( )
A.-eq \f(63,65) B.-eq \f(33,65)
C.eq \f(63,65) D.eq \f(33,65)
A [∵α为锐角,cs α=eq \f(12,13),∴sin α=eq \r(1-cs2α)=eq \f(5,13),
∵β为第三象限角,sin β=-eq \f(3,5),∴cs β=-eq \r(1-sin2β)=-eq \f(4,5),
∴cs(α-β)=cs αcs β+sin αsin β=eq \f(12,13)×eq \b\lc\(\rc\)(\a\vs4\al\c1(-\f(4,5)))+eq \f(5,13)×eq \b\lc\(\rc\)(\a\vs4\al\c1(-\f(3,5)))=-eq \f(63,65).]
3.已知cseq \b\lc\(\rc\)(\a\vs4\al\c1(α-\f(π,3)))=cs α,则tan α= .
eq \f(\r(3),3) [cseq \b\lc\(\rc\)(\a\vs4\al\c1(α-\f(π,3)))=cs αcs eq \f(π,3)+sin α·sineq \f(π,3)=eq \f(1,2)cs α+eq \f(\r(3),2)sin α=cs α,所以eq \f(\r(3),2)sin α=eq \f(1,2)cs α,所以eq \f(sin α,cs α)=eq \f(\r(3),3),即tan α=eq \f(\r(3),3).]
4.cs(α-35°)cs(α+25°)+sin(α-35°)sin(α+25°)= .
eq \f(1,2) [原式=cs[(α-35°)-(α+25°)]
=cs(-60°)=cs 60°=eq \f(1,2).]
5.已知sin α=-eq \f(4,5),sin β=eq \f(5,13),且180°<α<270°,90°<β<180°,求cs(α-β)的值.
[解] 因为sin α=-eq \f(4,5),180°<α<270°,
所以cs α=-eq \f(3,5).
因为sin β=eq \f(5,13),90°<β<180°,
所以cs β=-eq \f(12,13),
所以cs(α-β)=cs αcs β+sin αsin β
=eq \b\lc\(\rc\)(\a\vs4\al\c1(-\f(3,5)))×eq \b\lc\(\rc\)(\a\vs4\al\c1(-\f(12,13)))+eq \b\lc\(\rc\)(\a\vs4\al\c1(-\f(4,5)))×eq \f(5,13)
=eq \f(36,65)-eq \f(20,65)=eq \f(16,65).
学 习 目 标
核 心 素 养
1.了解两角差的余弦公式的推导过程.(重点)
2.理解用向量法导出公式的主要步骤.(难点)
3.熟记两角差的余弦公式的形式及符号特征,并能利用该公式进行求值、计算.(重点、易混点)
1. 通过两角差的余弦公式的推导,培养数学运算素养.
2. 借助公式的变形、正用、逆用,提升逻辑推理素养.
cs(60°-30°)
cs 60°
cs 30°
sin 60°
sin 30°
eq \f(\r(3),2)
eq \f(1,2)
eq \f(\r(3),2)
eq \f(\r(3),2)
eq \f(1,2)
cs(120°-60°)
cs 120°
cs 60°
sin 120°
sin 60°
eq \f(1,2)
-eq \f(1,2)
eq \f(1,2)
eq \f(\r(3),2)
eq \f(\r(3),2)
公式
cs(α-β)=cs αcs β+sin αsin β
适用条件
公式中的角α,β都是任意角
公式结构
公式右端的两部分为同名三角函数积,连接符号与左边角的连接符号相反
给角求值问题
给值(式)求值问题
给值求角问题
高中数学人教A版 (2019)必修 第一册5.5 三角恒等变换第1课时学案: 这是一份高中数学人教A版 (2019)必修 第一册5.5 三角恒等变换第1课时学案,文件包含正文docx、答案docx等2份学案配套教学资源,其中学案共6页, 欢迎下载使用。
2021学年5.5 三角恒等变换第1课时学案及答案: 这是一份2021学年5.5 三角恒等变换第1课时学案及答案,共12页。
人教A版 (2019)必修 第一册第五章 三角函数5.5 三角恒等变换第1课时学案: 这是一份人教A版 (2019)必修 第一册第五章 三角函数5.5 三角恒等变换第1课时学案,共9页。













