


初中数学北师大版九年级上册2 反比例函数的图象与性质背景图课件ppt
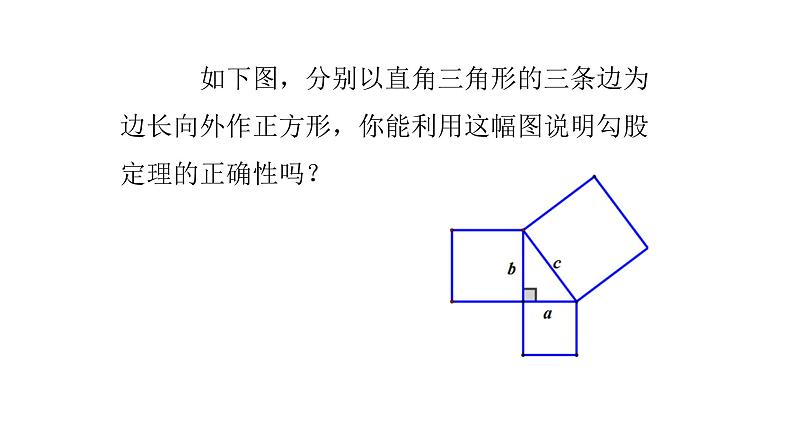
展开如下图,分别以直角三角形的三条边为边长向外作正方形,你能利用这幅图说明勾股定理的正确性吗?
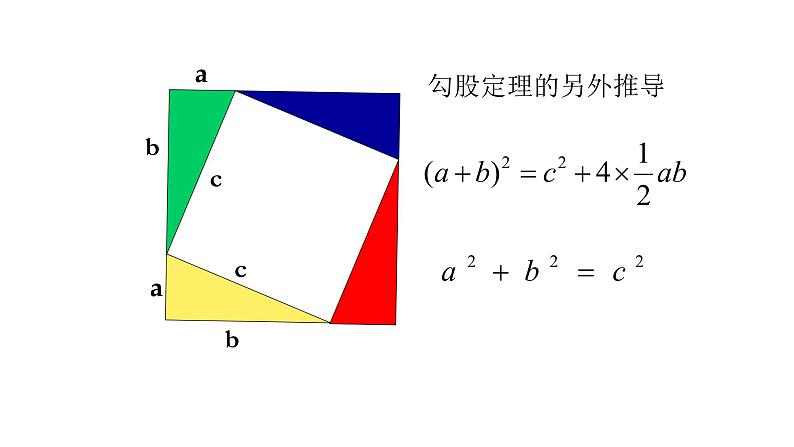
活动1:小明的证明思路如下图,想一想:小明是怎样对大正方形进行割补的?
你能将所有三角形和正方形的面积用a,b,c的关系式表示出来吗?
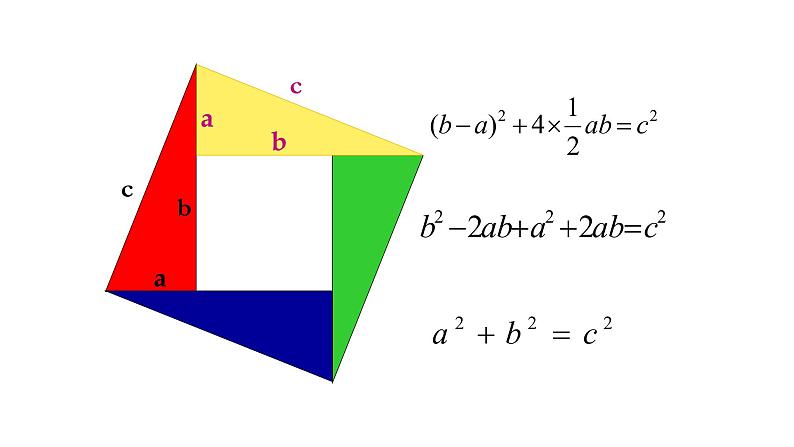
1876年4月1日,伽菲尔德在《新英格兰教育日志》上发表了他对勾股定理的这一证法。1881年,伽菲尔德就任美国第20任总统。后来,人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,就把这一证法称为“总统证法”。
证明:S梯形=2×0.5ab+0.5c2又S梯形=0.5(a+b)(a+b)∴0.5(a+b)(a+b)=2×0.5ab+0.5c2∴a2+b2=c2
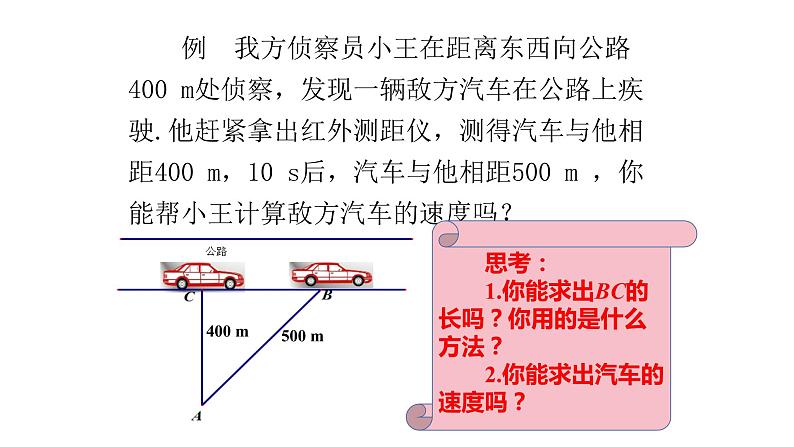
例 我方侦察员小王在距离东西向公路400 m处侦察,发现一辆敌方汽车在公路上疾驶.他赶紧拿出红外测距仪,测得汽车与他相距400 m,10 s后,汽车与他相距500 m ,你能帮小王计算敌方汽车的速度吗?
思考: 1.你能求出BC的长吗?你用的是什么方法? 2.你能求出汽车的速度吗?
例 我方侦察员小王在距离东西向公路400 m处侦察,发现一辆敌方汽车在公路上疾驶.他赶紧拿出红外测距仪,测得汽车与他相距400 m,10 s后,汽车与他相距500 m ,你能帮小王计算敌方汽车的速度吗?
观察下图,判断图中三角形的三边长是否满足a2+b2=c2.
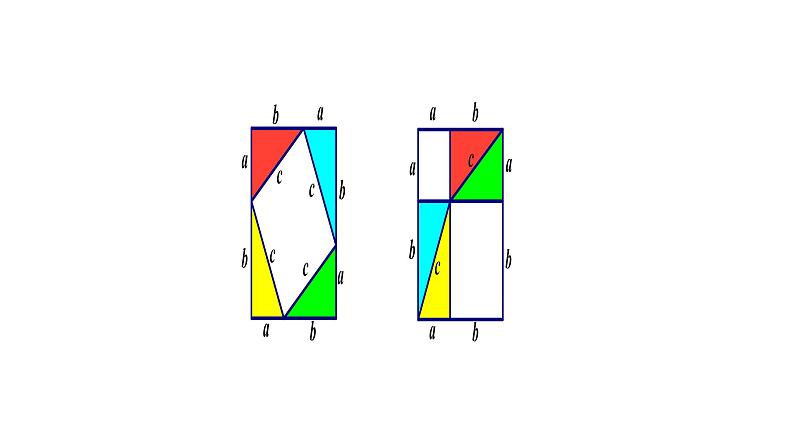
你是如何求出左侧图形中每个正方形的面积的?
结论1:若钝角三角形中较长边长为c,较短边长为a、b,则a2+b2
结论2:若锐角三角形中较长边长为c,较短边长为a、b,则a2+b2>c2.
随堂练习: 如图是某沿江地区交通平面图,为了加快经济发展,该地区拟修建一条连接M,O,Q三城市的沿江高速公路,已知沿江高速公路的建设成本为5 000万元/km,该沿江高速公路的造价预计是多少?
解:在Rt△MNO中,根据勾股定理得MN2 +NO2=MO2,∴302+ 402 =MO2,∴MO=50( km )同理: 0Q=130 km.∴总造价为:(50+130) ×5 000=900000(万元)答:估计总造价为900000万元
习题1.2 1,2,3,4
1.(2016湖南株洲中考)如图1-1-12,以直角三角形的边a、b、c为边,向外作等边三角形、半圆、等腰直角三角形和正方形,上述四种情况的面积关系满足S1+S2=S3的图形个数为 ( )
(1)第一个图形中,首先根据等边三角形的面积的求法,表示出3个等边三角形的面积,然后根据a2+b2=c2,可得S1+S2=S3.(2)第二个图形中,首先根据圆的面积的求法,表示出3个半圆的面积,然后根据a2+b2=c2,可得S1+S2=S3.(3)第三个图形中,首先根据等腰直角三角形的面积的求法,表示出3个等腰直角三角形的面积,然后根据a2+b2=c2,可得S1+S2=S3.(4)第四个图形中,首先根据正方形的面积的求法,表示出3个正方形的面积,然后根据a2+b2=c2,可得S1+S2=S3.故满足S1+S2=S3的图形个数为4.
∴a2+b2=c2=100.
∴(a+b)2-2ab=100.
∴142-2ab=100.
数学八年级上册1 探索勾股定理精品ppt课件: 这是一份数学八年级上册1 探索勾股定理精品ppt课件,共36页。
初中数学北师大版八年级上册1 探索勾股定理优质课件ppt: 这是一份初中数学北师大版八年级上册1 探索勾股定理优质课件ppt,共31页。PPT课件主要包含了勾股树,导入新知,素养目标,勾股定理的探索,做一做,探究新知,数格子,单位面积,4分析填表数据,勾股定理等内容,欢迎下载使用。
初中数学北师大版八年级上册1 探索勾股定理教案配套ppt课件: 这是一份初中数学北师大版八年级上册1 探索勾股定理教案配套ppt课件,共17页。PPT课件主要包含了探索勾股定理,Contents,情景导入,情境导入,新知探究,S浅蓝色正方形b2,S紫色正方形a2,S绿色正方形c2,c2a2+b2,巩固练习等内容,欢迎下载使用。













