初中数学人教版九年级上册21.2.2 公式法示范课课件ppt

这是一份初中数学人教版九年级上册21.2.2 公式法示范课课件ppt，共25页。PPT课件主要包含了温故知新，用配方法解方程，解方程可化为，∴方程无实数根，师生互动巩固新知，用公式法解下列方程，小结与反思，拓展延伸等内容，欢迎下载使用。

用配方法解一元二次方程的步骤
1.移项:把常数项移到方程的右边;2.二次项系数化为1：方程两边都除以二次项系数3.配方:方程两边都加上一次项系数绝对值一半的平方;4.变形:方程左边分解因式,右边合并同类项;5.开方:根据平方根意义,方程两边开平方;6.求解:解两个一元一次方程;7.定解:写出原方程的解.
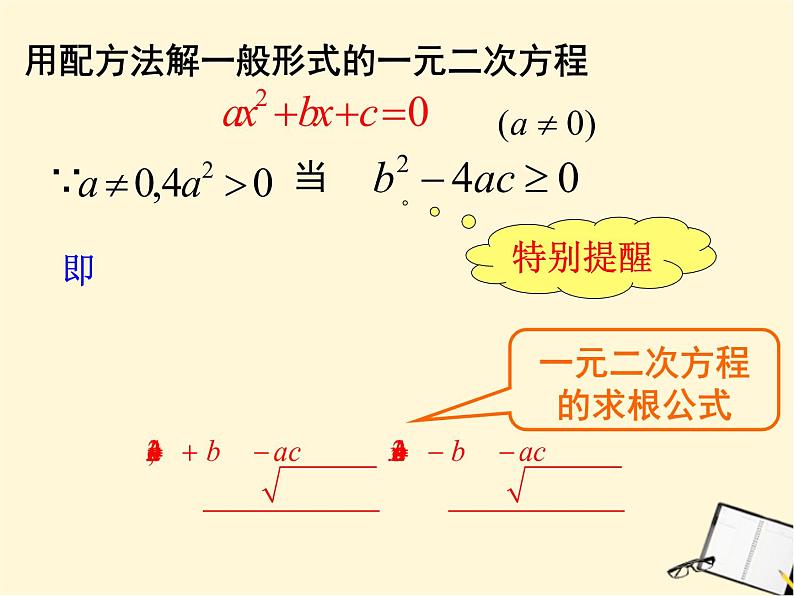
请问：一元二次方程的一般形式是什么？
方程两边都除以　，得
一元二次方程的求根公式
由上可知，一元二次方程
的根由方程的系数a，b，c确定．因此，解一元二次方程时，可以先将方程化为一般形式 ，当
就得到方程的根，这个式子叫做一元二次方程的求根公式，利用它解一元二次方程的方法叫做公式法，由求根公式可知，一元二次方程最多有两个实数根。
时，将a，b，c 代入式子
（2）当 时，有两个相等的实数根。
（1）当 时，有两个不等的实数根。
（3）当 时，没有实数根。
一元二次方程的根的情况
一般的，式子 b2-4ac 叫做一元二次方程根的判别式，通常用希腊字母“∆”来表示，即∆＝b2-4ac
例1.已知一元二次方程2x2﹣5x+3=0，则该方程根的情况是（　　）A．有两个不相等的实数根 B．有两个相等的实数根C.两个根都是自然数 D．无实数根
1.根据根的判别式判断一元二次方程根的情况
练1．已知：关于x的方程x2+2mx+m2﹣1=0（1）不解方程，判别方程根的情况；（2）若方程有一个根为3，求m的值．
例2、关于x的一元二次方程kx2-2x-1=0有两个不等的实根，则k的取值范围是 （ ）
A.k>-1 B. k>-1 且k≠ 0 C. k<1 D. k<1 且k≠0
解:∵ ＞0∴k＞-1
又∵k≠0 ∴ k＞-1且k≠0
2.根据一元二次方程根的情况求参数的值或取值范围
注意：一元二次方程有实根，说明方程可能有两个不等实根或两个相等实根的两种情况。
练2．关于x的一元二次方程（m-2）x2+2x+1=0有实数根，则m的取值范围是（　　）A．m≤3 B．m＜3 C．m＜3且m≠2 D．m≤3且m≠2
例3　用公式法解下列方程：　（１）x2 - 4x -7=0
a=1, b= -4 ,c= -7
∆=b2 - 4ac =12 - 4×1×(-7)=44>0
3.公式法解一元二次方程
用公式法解一元二次方程的一般步骤：
求本章引言中的问题，雕像下部高度x(m)满足方程
精确到0.001，x1≈ 1.236，x2≈ －3.236
但是其中只有x1≈1.236符合问题的实际意义，所以雕像下部高度应设计为约1.236m。
1、一元二次方程的求根公式是用什么方法推导出来的？2、试默写一元二次方程的求根公式；试说出根的判别式；如何用根的判别式判定一元二次方程根的情况？3、说出用公式法解一元二次方程的一般步聚4、你有什么疑惑或想法？
作业：教科书p17 4、(2)、(4)5、（３）、（４）配方法　（５）、（６）公式法
1.已知关于x的一元二次方程kx2﹣2（k﹣1）x+k﹣2=0（k≠0）（1）小明考查后说，它总有两个不相等的实数根；（2）小华补充说，其中一个根与k无关．
2.请你说说其中的道理．已知关于x的一元二次方程mx2﹣（m+2）x+2=0；（1）证明：不论m为何值时，方程总有实数根；（2）m为何整数时，方程有两个不相等的正整数根．