九年级上册第二十五章 概率初步综合与测试复习课件ppt

这是一份九年级上册第二十五章 概率初步综合与测试复习课件ppt，共27页。PPT课件主要包含了要点梳理，确定事件，随机事件，必然事件，不可能事件，概率的概念，概率的值，列表法，树形图的画法，一个试验等内容，欢迎下载使用。

一、事件的分类及其概念
　1.在一定条件下必然发生的事件，叫做必然事件；　2.在一定条件下不可能发生的事件，叫做不可能事件；　3.在一定条件下可能发生也可能不发生的事件，叫做随 机事件.
1.概率： 一般地，对于一个随机事件A，我们把刻画其发生可能性大小的数值，称为随机事件A发生的概率，记作P（A）.
事件发生的可能性越来越大
事件发生的可能性越来越小
三、随机事件的概率的求法
1.①当实验的所有结果不是有限个，或各种可能结果发生的可能性不相等时，我们用大量重复试验中随机事件发生的稳定频率来估计概率.
②频率与概率的关系：两者都能定量地反映随机事件可能性的大小，但频率具有随机性，概率是自身固有的性质，不具有随机性.
2.概率的计算公式： 一般地，如果在一次试验中，有n种可能的结果，并且它们发生的可能性都相等，那么出现每一种结果的概率都是 . 如果事件A包括其中的m种可能的结果，那么事件A发生的概率
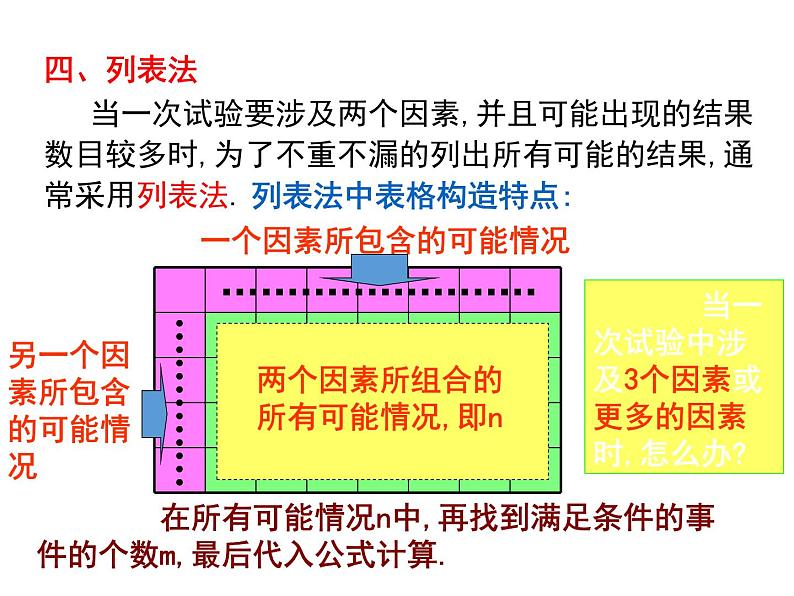
当一次试验要涉及两个因素,并且可能出现的结果数目较多时,为了不重不漏的列出所有可能的结果,通常采用列表法.
一个因素所包含的可能情况
另一个因素所包含的可能情况
两个因素所组合的所有可能情况,即n
在所有可能情况n中,再找到满足条件的事件的个数m,最后代入公式计算.
列表法中表格构造特点:
当一次试验中涉及3个因素或更多的因素时,怎么办?
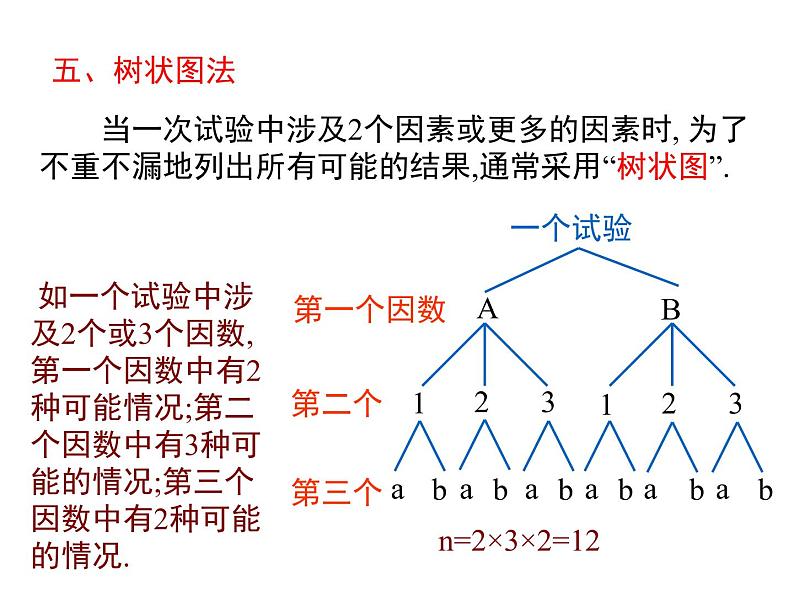
当一次试验中涉及2个因素或更多的因素时, 为了不重不漏地列出所有可能的结果,通常采用“树状图”.
如一个试验中涉及2个或3个因数,第一个因数中有2种可能情况;第二个因数中有3种可能的情况;第三个因数中有2种可能的情况.
例1 下列事件是随机事件的是（ ）A.明天太阳从东方升起 B.任意画一个三角形，其内角和是360°C.通常温度降到0℃以下，纯净的水结冰D.射击运动员射击一次，命中靶心
1.“闭上眼睛从布袋中随机地摸出1个球，恰是红球的概率是 ”的意思是（ ）A．布袋中有2个红球和5个其他颜色的球B．如果摸球次数很多，那么平均每摸7次，就有2次摸中红球C．摸7次，就有2次摸中红球D．摸7次，就有5次摸不中红球
2.下列事件中是必然事件的是（　　）A．从一个装有蓝、白两色球的缸里摸出一个球，摸出的球是白球B．小丹的自行车轮胎被钉子扎坏C．小红期末考试数学成绩一定得满分D．将油滴入水中，油会浮在水面上
例2 如图，电路图上有四个开关A、B、C、D和一个小灯泡，闭合开关D或同时闭合开关A、B、C都可使小灯泡发光，则任意闭合其中两个开关，小灯泡发光的概率是（ ） A. B. C. D.
例3 如图所示，有3张不透明的卡片，除正面写有不同的数字外，其它均相同．将这三张卡片背面朝上洗匀后，第一次从中随机抽取一张，并把这张卡片标有的数字记作一次函数表达式中的k，第二次从余下的两张卡片中再随机抽取一张，上面标有的数字记作一次函数表达式中的b．（1）写出k为负数的概率；（2）求一次函数y=kx+b的图象经过 二、三、四象限的概率.
解：（1）P（k为负数）= .
【解析】（1）因为－1，－2，3中有两个负数，故k为负数的概率为 ；（2）由于一次函数y=kx+b的图象经过二、三、四象限时，k，b均为负数，所以在画树形图列举出k、b取值的所有情况后，从中找出所有k、b均为负数的情况，即可得出答案．
（2）画树状图如右：由树状图可知，k、b的取值共有6种情况，其中k＜0且b＜0的情况有2种，∴P（一次函数y=kx+b的图象经过第二、三、四象限）= .
3. 一个袋中装有2个黑球3个白球，这些球除颜色外，大小、形状、质地完全相同，在看不到球的情况下，随机的从这个袋子中摸出一个球不放回，再随机的从这个袋子中摸出一个球，两次摸到的球颜色相同的概率是(　　) A. B. C. D.
例4 在大量重复试验中，关于随机事件发生的频率与概率，下列说法正确的是（ ）A.频率就是概率 B.频率与试验次数无关 C.概率是随机的，与频率无关 D.随着试验次数的增加，频率一般会越来越接近概率
例5 在一个不透明的布袋中，红色、黑色、白色的玻璃球共有40个，除颜色外其他完全相同，小明通过多次摸球试验后发现从中摸到红色球、黑色球的频率稳定在15％和45％，则口袋中白色球的个数最有可能是（ ） A.24个 B.18个 C.16个 D.6个
4.在一个不透明的口袋中，装有若干个除颜色不同其余都相同的球．如果口袋中装有３个红球且摸到红球的概率为 ，那么口袋中球的总个数为_____．
解析：设口袋中球的总个数为x， 则摸到红球的概率为 ， 所以x=15．
例6 在一个不透明的口袋里分别标注2、4、6的3个小球（小球除数字外，其余都相同），另有3张背面完全一样，正面分别写有数字6、7、8的卡片.现从口袋中任意摸出一个小球，再从这3张背面朝上的卡片中任意摸出一张卡片.（1）请你用列表或画树状图的方法，表示出所有可能出现的结果；
（2）小红和小莉做游戏，制定了两个游戏规则：规则1：若两次摸出的数字，至少有一次是“6”，小红赢；否则，小莉赢；规则2：若摸出的卡片上的数字是球上数字的整数倍时，小红赢；否则，小莉赢.小红想要在游戏中获胜，她会选择哪一条规则，并说明理由.
规则1：P(小红赢）= ；规则2：P(小红赢）= ∵ ， ∴小红选择规则1.
5.A、B两个小型超市举行有奖促销活动，顾客每购满20元就有一次按下面规则转动转盘获奖机会，且两超市奖额等同.规则是： ①A超市把转盘甲等分成4个扇形区域、B超市把转盘乙等分成3个扇形区域，并标上了数字（如图所示）； ②顾客第一回转动转盘要转两次，第一次与第二次分别停止后指针所指数字之和为奇数时就获奖（若指针停在等分线上，那么重转一次，直到指针指向某一份为止）.
解：（1）列表格如下：
共有16种等可能结果，其中中奖的有8种；
（1）利用树形图或列表法分别求出A、B两超市顾客一回转盘获奖的概率；
共有9种等可能结果，其中中奖的有4种；
（2）如果只考虑中奖因素，你将会选择去哪个超市购物？说明理由.
（2）选甲超市.理由如下：∵P(甲）>P(乙）， ∴选甲超市.
刻画随机事件发生可能性大小的数值
适合于两个试验因素或分两步进行
适合于三个试验因素或分三步进行
在大量重复试验中，频率具有稳定性时才可以用来估计概率