初中17.2 勾股定理的逆定理备课课件ppt

这是一份初中17.2 勾股定理的逆定理备课课件ppt，共16页。PPT课件主要包含了学习目标，温故知新，例题教学等内容，欢迎下载使用。

1.灵活应用勾股定理及其逆定理解决实际问题.（重点）2．进一步加深性质定理与判定定理之间关系的认识。3.将实际问题转化成用勾股定理的逆定理解决的数学问 题.（难点）
2.你能用勾股定理及其逆定理解决哪些问题？
1.我们已经学习了勾股定理及其逆定理，你能叙述吗？
如果三角形的三边长a、b、c满足 a2 + b2 = c2 那么这个三角形是直角三角形。
勾股定理的逆定理的内容和作用是什么？
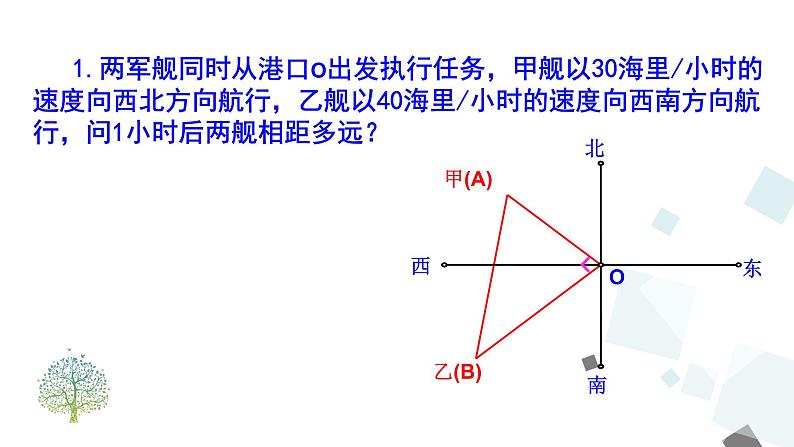
1.两军舰同时从港口O出发执行任务，甲舰以30海里/小时的速度向西北方向航行，乙舰以40海里/小时的速度向西南方向航行，问1小时后两舰相距多远？
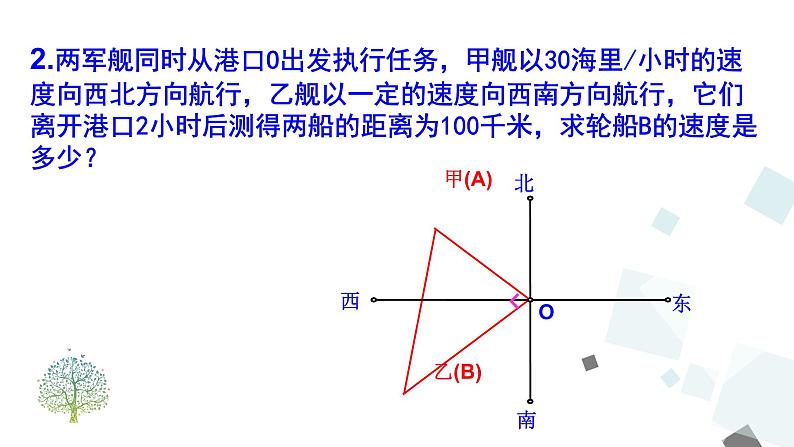
2.两军舰同时从港口O出发执行任务，甲舰以30海里/小时的速度向西北方向航行，乙舰以一定的速度向西南方向航行，它们离开港口2小时后测得两船的距离为100千米，求轮船B的速度是多少？
例1 如图，某港口P位于东西方向的海岸线上．“远航”号、“海天”号轮船同时离开港口，各自沿一固定方向航行，“远航”号每小时航行16 n mile，“海天”号每小时航行12 n mile ．它们离开港口一个半小时后分别位于点Q，R处，且相距30 n mile ．如果知道“远航”号沿东北方向航行，能知道“海天”号沿哪个方向航行吗？
问题1 认真审题，弄清已知是什么？要解决的问题是什么？
“远航”号的航向、两艘船的一个半小时后的航程及距离已知，如图.
问题2 由于我们现在所能得到的都是线段长，要求角，由此你联想到了什么？
实质是要求出两艘船航向所成角.
PQ=16×1.5=24(海里),
PR=12×1.5=18(海里),
∵242+182=302，即PQ2+PR2=QR2,∴∠QPR=90°.
由“远航”号沿东北方向航行可知∠1=45°.∴∠2=45°，即“海天”号沿西北方向航行.
归纳:解决实际问题的步骤：构建几何模型(从整体到局部)； 标注有用信息,明确已知和所求；应用数学知识求解.
1、A、B、C三地的两两距离如图所示，A地在B地的正东方向，C地在B地的什么方向？
解：∵ BC2+AB2=52+122=169AC2 =132=169∴BC2+AB2=AC2即△ABC是直角三角形∠B=90°答：C在B地的正北方向．
2、小明向东走80m后，又向某一方向走60m后，再沿第三个方向又走100m回到原地．小明向东走80m后又向哪个方向走的？
小明向东走80m后又向正南方向走的或又向正北方向走的
3、已知：如图，四边形ABCD中，AB＝3，BC＝4，CD＝12，AD＝13, ∠B＝900，求四边形ABCD的面积?
解：连接AC∵ ∠B＝90° AB＝3，BC＝4，∴AC= =5在△ACD中，AC²+CD²=25+144=169=AD²， ∴△ACD是直角三角形， ∴∠ACD=90°； ∴S四边形ABCD= S△ABC+ S△ACD=36．
4. 如图,点A是一个半径为 400 m的圆形森林公园的中心,在森林公园附近有 B .C 两个村庄,现要在 B.C 两村庄之间修一条长为 1000 m 的笔直公路将两村连通,经测得 ∠B=60°,∠C=30°,问此公路是否会穿过该森林公园?请通过计算说明.
已知a、b、c为△ABC的三边,且 满足 a2+b2+c2+338=10a+24b+26c. 试判断△ABC的形状.
分析：先变形后根据非负性性质求出a，b，c的值，最后根据勾股定理的逆定理判断。