






所属成套资源:2024-2025学年北师大(2024)版数学七年级下册 课件
数学七年级下册(2024)1 幂的乘除课文ppt课件
展开
这是一份数学七年级下册(2024)1 幂的乘除课文ppt课件,共18页。PPT课件主要包含了学习目标,新课导入,幂的意义,同底数幂的乘法法则,102×3,102+2+2,新知探究,提出问题,乘方的意义,乘法的意义等内容,欢迎下载使用。
1.理解幂的乘方的运算性质,进一步体会和巩固幂的意义。【重点】2.掌握幂的乘方法则的推导过程并能灵活应用。【难点】
地球、木星、太阳可以近似地看作球体。木星、太阳的半径分别约是地球的10倍和102倍,它们的体积分别约是地球的_______倍和_______倍。
你知道(102)3 等于多少吗?
思考:(am)n =? 其中m,n都是正整数。
(102)3 =102×102×102
( )
( )
知识点 幂的乘方法则
计算下列各式,并说明理由。(1)( 62 )4; (2)( a2 )3; (3)( am )2。
(3) ( am )2 =am · am=am+m=a2m。
解:(1) ( 62 )4 =62×62×62×62 =62+2+2+2 =68 =62×4。
(2) ( a2 )3 =a2 ·a2 · a2=a2+2+2=a6=a2×3。
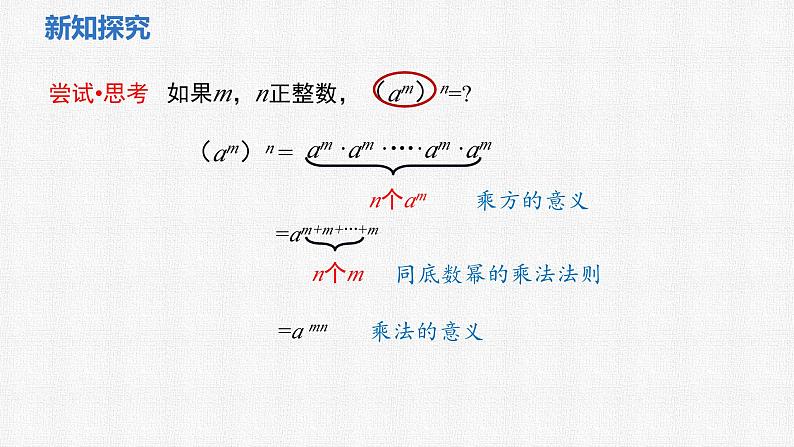
尝试•思考 如果m,n正整数,(am)n=?
am ·am ·…·am ·am
注意:1.“底数不变”是指幂的底数a不变,“指数相乘”是指幂的指数m与乘方的指数n相乘。2.底数可以是具体的数,也可以是代数式。
(am)n = amn (m,n 都是正整数)。
幂的乘方,底数 ,指数 。
计算:(1) (102)3; (2)(b5)5;
解:(1)(102)3=102×3=106。
(2)(b5)5=b5×5=b25。
(3)[(x-2y)3]4=(x-2y)3×4=(x-2y)12。
(3)[(x-2y)3]4;
(4)-(x2)m;
(5)(y2)3·y;
(4)-(x2)m=-x2×m=-x2m。
(5)(y2)3·y=y2×3·y=y6·y=y7。
(6)2(a2)6–(a3)4=2a2×6-a3×4=2a12–a12=a12。
(6)2(a2)6-(a3)4。
解:(1)(103)3=109。
(3)(x3)4·x2=x12·x2=x14。
2.判断下面计算是否正确?如果有错误请改正:(1)(x5)5=x10; ( )(2)a6·a4=a24; ( ) (3)m6+m4=m10; ( ) (4) 2y6+y6=3y 12。 ( )
改正:(x5)5=x25。
改正:a6·a4=a10。
改正:2y6+y 6=3y6。
想一想:同底数幂的乘法法则与幂的乘方法则有什么相同 点和不同点?
知识点 幂的乘方法则的逆用
例2 比较340与430的大小。
解:因为340=(34)10,430=(43)10,且34=81,43=64,81>61,所以(34)10>(43)10,即340>430。
1.已知10m=3,10n=2,求下列各式的值:(1)103m;(2)102n;(3)103m+2n。
(3)103m+2n=103m×102n=27×4=108。
解:(1)103m=(10m)3=33=27。
(2)102n=(10n)2=22=4。
2.已知 2x+5y-3=0,求 4x · 32y 的值。
解:因为 2x+5y-3=0,所以2x+5y=3,所以4x · 32y=(22)x · (25)y =22x · 25y=22x+5y=23=8。
(am)n=amn (m,n都是正整数)
幂的乘方:底数不变,指数相乘
幂的乘方与同底数幂的乘法的区别:(am)n=amn;am ﹒an=am+n
幂的乘方法则的逆用:amn=(am)n=(an)m(m,n都是正整数)
1.判断题,错误的予以改正。 (1)a4+a4=2a8; ( )(2)(x3)3=x6; ( )(3)(-4)2×(-4)4=(-4)6=-46; ( )(4)[(m-n)4]3-[(m-n)6]2=0。 ( )
改正:a4+a4=2a4。
改正:(x3)3=x9。
2.若(x2)m=x10,则m= 。
相关课件
这是一份北师大版(2024)七年级下册(2024)第一章 整式的乘除1 幂的乘除背景图课件ppt,共16页。PPT课件主要包含了幂的意义,am·an,am+n,等于多少呢,amn,am+m++m,n个am,n个m,幂的乘方法则,底数不变等内容,欢迎下载使用。
这是一份数学七年级下册(2024)1 幂的乘除评课课件ppt,共20页。PPT课件主要包含了同底数幂的乘法法则,幂的意义,102+2+2,102×3,根据幂的意义,62+2+2+2,62×4,am+m++m,amn,n个am等内容,欢迎下载使用。
这是一份初中数学北师大版七年级下册第一章 整式的乘除2 幂的乘方与积的乘方图片课件ppt,共24页。PPT课件主要包含了学习目标,复习回顾,问题情境,探究新知,典型例题,随堂练习,-2a2b3,课堂小结等内容,欢迎下载使用。









