北师大版（2024）八年级下册2 平行四边形的判定示范课ppt课件

这是一份北师大版（2024）八年级下册2 平行四边形的判定示范课ppt课件，共16页。PPT课件主要包含了OBOD，就能说明四边形，自学检测28分钟，∴OEOF，AB∥CDAD∥BC，ABCDADBC，OAOCOBOD，ABCDAB∥CD，小结1分钟，当堂训练12分钟等内容，欢迎下载使用。
6.2.2平行四边形的判定
1.探索并掌握平行四边形的另外一种判别方法。2.能运用平行四边形的判别方法和性质解决简单的实际问题。
自学指导1（1分钟）：自学课本P143-144例2之前的内容，思考并解决下列问题：解决课本P143的问题，由此得出平行四边形的判定定理是什么？几何语言表示为：
∵AO=CO，BO=DO∴四边形ABCD是平行四边形
教师巡视，学生自学（5分钟）
两条对角线互相平分的四边形是平行四边形
2、下列条件中,不能判别四边形ABCD是平行四边形的 是（ ） A.∠A=∠B=∠C=90° B.∠A+∠B=180°，∠B+∠C=180° C.∠A=∠C，∠B=∠D D.∠A+∠B=180°，∠C+∠D=180°
或AD∥BC或AB∥CD
或∠OAD=∠OCB或∠ODA=∠OBC等
1、如图，若对角线AC、BD相交于点O，且OA=OC，则只需添加一个条件 —————————————————
自学检测1（4分钟）：
ABCD是平行四边形。
自学指导2（1分钟）：自学课本P144例2的内容，思考并解决下列问题：
1、认真阅读例题2，例2中用了哪些定理？
2、归纳平行四边形的所有判定定理
教师巡视，学生自学（4分钟）
（1）运用了平行四边形的性质定理：平行四边形的对角线互相平分；
（2）运用了平行四边形的判定定理：对角线互相平分的四边形是平行四边形；
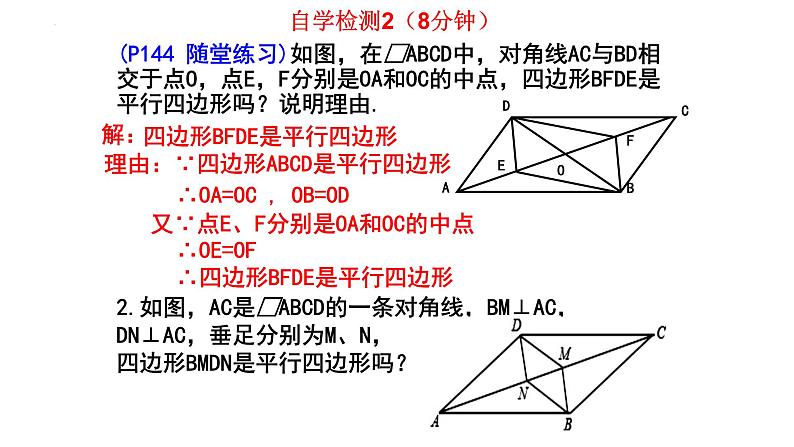
(P144 随堂练习)如图，在□ABCD中，对角线AC与BD相交于点O，点E，F分别是OA和OC的中点，四边形BFDE是平行四边形吗？说明理由.
理由：∵四边形ABCD是平行四边形
∴OA=OC , OB=OD
又∵点E、F分别是OA和OC的中点
∴四边形BFDE是平行四边形
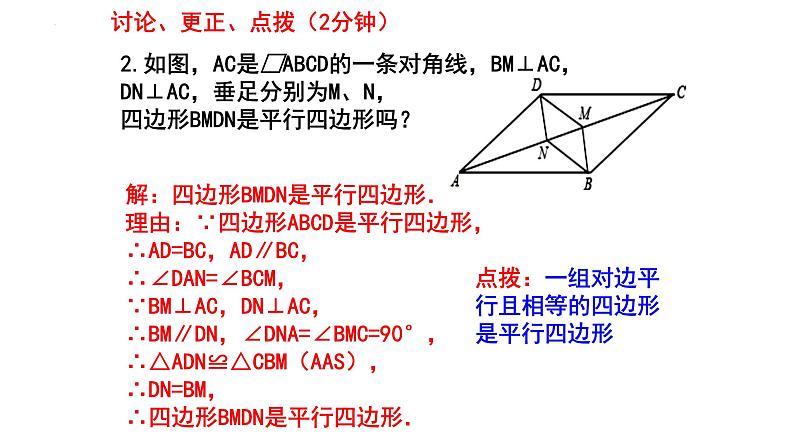
2.如图，AC是□ABCD的一条对角线，BM⊥AC，DN⊥AC，垂足分别为M、N，四边形BMDN是平行四边形吗？
四边形BFDE是平行四边形
解：四边形BMDN是平行四边形．理由：∵四边形ABCD是平行四边形，∴AD=BC，AD∥BC，∴∠DAN=∠BCM，∵BM⊥AC，DN⊥AC，∴BM∥DN，∠DNA=∠BMC=90°，∴△ADN≌△CBM（AAS），∴DN=BM，∴四边形BMDN是平行四边形．
讨论、更正、点拨（2分钟）
点拨：一组对边平行且相等的四边形是平行四边形
平行四边形判别方法有哪些？
两组对边分别平行的四边形是平行四边形
一组对边平行且相等的四边形是平行四边形
两组对边分别相等的四边形是平行四边形
四边形ABCD是平行四边形
1.如图,□ ABCD的对角线AC与BD相交于点O，点E、F分别在OB和OD上（1）当BE,DF满足 条件时，四边形AECF是平行四边形;（2）当∠AEB与∠CFD满足 条件时，四边形AECF是平行四边形.
∠AEB=∠CFD
2.已知：AD为△ABC的角平分线，DE∥AB ，在AB上截取BF＝AE,求证：EF＝BD3.P145 问题解决3
3 （1）是，因为此时EO=GO,FO=HO （2）是，道理与（1）相同。 （3）同理
解：设t秒后四边形ABNM是平行四边形 则AM=BN,即， t=6-2t, 解得，t=2当t=2秒时，AM=BN=2且AM∥BN,所以四边形ABNM是平行四边形。
解：∵a2+b2+c2+d2=2(ac+bd) ∴ (a2-2ac+c2)+(b2-2bd+d2)=0 ∴(a-c)2+(b-d)2=0 ∵（a-c)2≥0,(b-d)2≥0 ∴a-c=0,b-d=0,即，a=c,b=d ∴当a与c,b与d为对边时，四边形是平行四边形。
注意： 对边分别相等是平行四边形， 邻边相等不一定是平行四边形
（选做题2）已知四边形的四条边长分别为a,b,c,d,且满足a2+b2+c2+d2=2(ac+bd),四边形是平行四边形吗？
平行四边形的判定方法：
3、一组对边平行且相等的四边形是平行四边形；
2、两组对边分别相等的四边形是平行四边形；
1、两组对边分别平行的四边形是平行四边形；
4、对角线互相平分的四边形是平行四边形；
∴四边形ABCD是平行四边形
在△AOD和△BOC中
∴ △AOD ≌ △BOC（SAS）
∴ AD=BC, ∠ADO=∠CBO
已知：在四边形ABCD中，对角线AC、BD相交于点O 且AO=CO，BO=DO.
试说明：四边形ABCD是平行四边形