





数学八年级下册2 平行四边形的判定优质课ppt课件
展开北师大版八年级数学下册
《6.2平行四边形的判定第1课时》教学设计
课题名 | 6.2平行四边形的判定(第1课时) |
教学目标 | 1.知识与技能:掌握平行四边形判定方法,平行四边形判定方法的理解和灵活应用. 2.过程与方法:在拼摆平行四边形的过程中,培养学生的动手实践能力及丰富的想象力,积累数学活动经验,增强学生的创新意识. 3.情感态度和价值观:体会证明过程中的类比、转化等数学思想,培养学生面对挑战,勇于克服的学习热情. |
教学重点 | 平行四边形判定定理的探究,运用平行四边形的判定定理解决问题. |
教学难点 | 对平行四边形判定方法的探究以及平行四边形的性质和判定的综合运用. |
教学准备 | 教师准备:课件、三角尺 学生准备:三角尺及常规用具 |
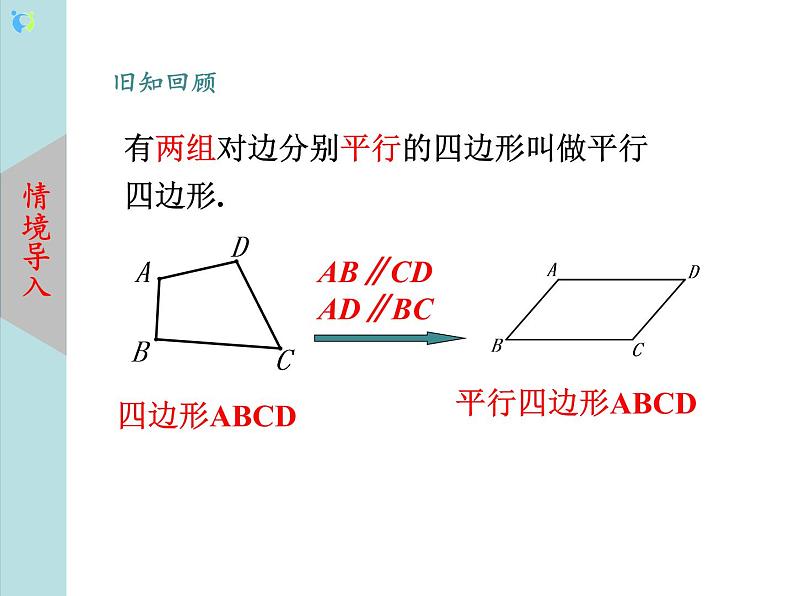
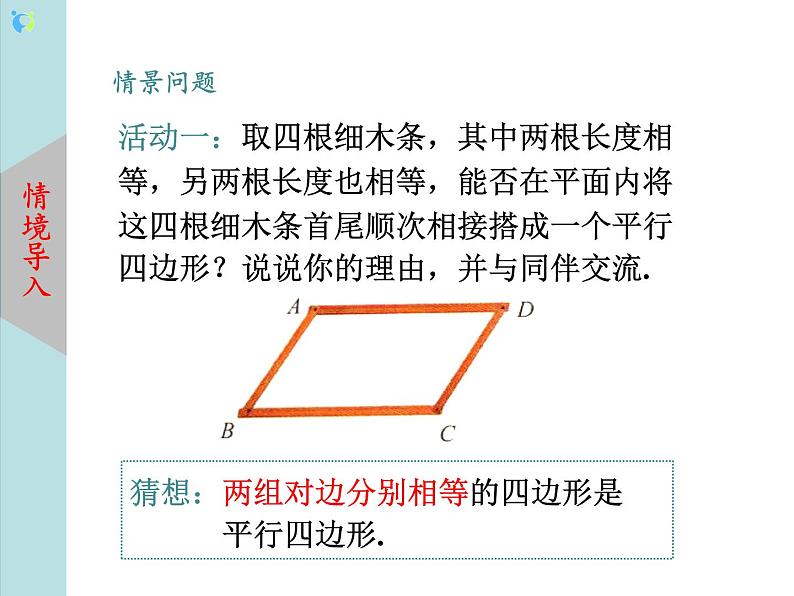
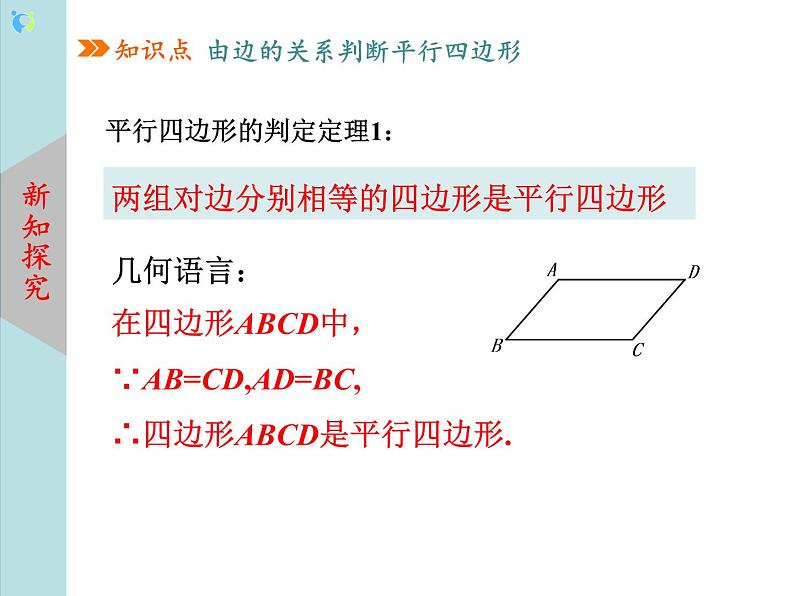
教学过程 | 一、 新课导入 情景问题:活动一:取四根细木条,其中两根长度相等,另两根长度也相等,能否在平面内将这四根细木条首尾顺次相接搭成一个平行四边形?说说你的理由,并与同伴交流. 猜想:两组对边分别相等的四边形是平行四边形. 教师预设学生回答: 1.选择相等的两根木条作为对边,并且只有将两两相等的木条分别作为四边形的两组对边才能摆出平行四边形. 2.有两组对边分别相等的四边形一定是平行四边形. 3.连接对角线,利用三角形全等和平行四边形的定义证明. 学生利用课前准备好的学具动手操作、观察,完成探究活动,共同得到: (1)只有将两两相等的木条分别作为四边形的两组对边才能得到平行四边形. (2)通过观察、实验、猜想到:两组对边分别相等的四边形是平行四边形. 设计意图:情境问题从日常生活实际入手,根据学生的认知基础,学生会较快地回答出利用的是平行四边形的定义,不仅引入了新课,也激发了学生的学习兴趣.教师借机与学生共同回顾定义的双重作用,即定义可以当性质定理用,也可以当判定定理用. 二、 新知讲授 知识点一:平行四边形的判定定理1 已知: 四边形ABCD中,AB=DC,AD=BC. 求证: 四边形ABCD是平行四边形. 平行四边形的判定定理1: 两组对边分别相等的四边形是平行四边形 几何语言: 在四边形ABCD中, ∵AB=CD,AD=BC, ∴四边形ABCD是平行四边形. 学生独立推理,得出正确结论,体会对判定方法. 设计意图:关于判定定理证明的方法,即连接辅助线将平行四边形转化成三角形问题来证明.根据学生的认知水平,教师应加以适当引导分析并规范书写推理论证的过程. 例1 如图,已知四边形ABCD是平行四边形,DE平分∠ADC,交CB的延长线于点E,BF平分∠ABC,交AD的延长线于点F.
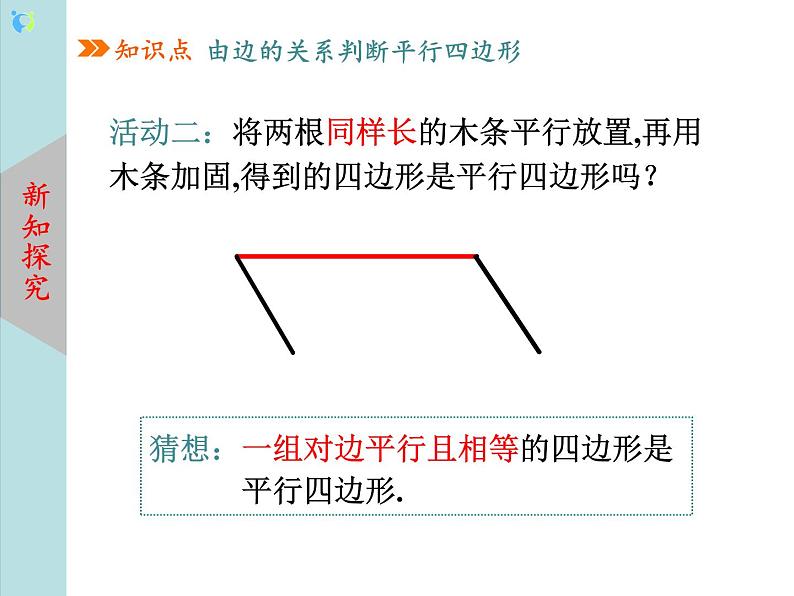
设计意图:通过例题,促进学生对定理条件的掌握.. 知识点二:平行四边形的判定定理2 活动二:将两根同样长的木条平行放置,再用木条加固,得到的四边形是平行四边形吗? 猜想:一组对边平行且相等的四边形是平行四边形. 学生活动:利用课前准备好的学具动手操作、观察,完成探究活动,得出猜想命题. 设计意图:通过观察、猜想,经历知识的发展形成过程,体验了“发现”知识的快乐,变被动接受为主动探究. 已知:如图,在四边形ABCD中,AB∥CD,AB=CD. 求证:四边形ABCD是平行四边形.
平行四边形的判定定理2: 一组对边平行且相等的四边形是平行四边形 几何语言: 在四边形ABCD中, ∵AD∥BC,AD=BC, ∴四边形ABCD是平行四边形. 学生类比知识点一的探究过程,独立证完成,并归纳得出判定定理2. 设计意图:为学生创设探究活动,给学生提供问题空间,提升学生的学习能力. 例2 如图,在▱ABCD中,E,F分别是AB,CD的中点. 求证:四边形EBFD是平行四边形.
变式 :已知:如图,在□ABCD中,点E,F分别在AB和CD上,BE=DF. 求证:四边形AECF是平行四边形.
设计意图:例题的讲解不仅巩固判定定理,也进一步巩固证明的书写格式. 三、 知识巩固 1.在四边形ABCD中,从①AB∥CD;②AB=CD; ③BC∥AD;④BC=AD中,任选两个使四边形ABCD为平行四边形的选法有( ) A.3种 B.4种 C.5种 D.6种 2.在四边形ABCD中,AB∥CD,要使四边形ABCD是平行四边形,下列添加的条件不正确的是( ) A.AB=CD B.BC=AD C.∠A=∠C D.BC∥AD 3. 横格纸的横线是互相平行的,在一条横线上截取线段AB= 25 mm,在另一条横线上按照同一方向截取CD=25 mm,连结AC,BD,那么四边形ACDB一定是平行四边形,理由是___________________________________. 4. 如图,在四边形ABCD中,AB=CD,过点A作AE⊥BD交BD于点E,过点C作CF⊥BD交BD于点F,且AE=CF. 求证:四边形ABCD是平行四边形.
5. 如图,在▱ABCD中,E,F分别是AD,BC的中点,AF与EB相交于点G,CE与DF相交于点H,试说明四边形EGFH为平行四边形.
拓展练习:6.如图,在四边形ABCD中,AD∥BC,BC=6 cm,AD=9 cm.点P以1 cm/s的速度由A点向D点运动,同时点Q以2 cm/s的速度由C点向B点运动,当点P,Q运动 s时,直线QP将四边形ABCD截出一个平行四边形.
四、 课堂小结 平行四边形的判定方法: 定义法:两组对边分别平行的四边形是平行四边形. 判定定理1:两组对边分别相等的四边形是平行四边形. 判定定理2:一组对边平行且相等的四边形是平行四边形. |
布置作业 | 教材142-143页1,4题 |
板书设计 | 6.2平行四边形的判定(第1课时) 平行四边形的判定方法: 定义法:两组对边分别平行的四边形是平行四边形. 判定定理1:两组对边分别相等的四边形是平行四边形. 判定定理2:一组对边平行且相等的四边形是平行四边形. |
教学反思 | 问题的探究始终遵循学生的认知规律:从直观感受后的猜想到严谨的推理证明,让学生感受每一个结论都要有相应的依据.同时已有的定义和定理可以做为新问题的判定依据,感受数学的转化思想. 判定方法的得出都非常重视知识的发生、形成过程,让学生亲历了类比、观察、实验、猜想、验证、推理的整个过程,培养学生的探究能力,发展学生的合情推理能力.学生把所学知识加以灵活地运用,有效地激发了学生的学习兴趣,提高了学习效率.数学的学习要重视学习方法的指导.本节课通过由浅入深的练习和灵活的变式,引导学生抓住图形的基本特征和题目的内在联系,达到触类旁通的效果. |
数学八年级下册2 平行四边形的判定教学ppt课件: 这是一份数学八年级下册2 平行四边形的判定教学ppt课件,文件包含北师大版数学八年级下册62平行四边形的判定第1课时同步课件pptx、北师大版数学八年级下册62平行四边形的判定第1课时教学设计含教学反思docx等2份课件配套教学资源,其中PPT共26页, 欢迎下载使用。
初中数学北师大版八年级下册第六章 平行四边形2 平行四边形的判定教学课件ppt: 这是一份初中数学北师大版八年级下册第六章 平行四边形2 平行四边形的判定教学课件ppt,共17页。PPT课件主要包含了复习引入,定理探索,例题讲解,随堂练习,回顾小结,布置作业等内容,欢迎下载使用。
北师大版八年级下册2 平行四边形的判定完美版课件ppt: 这是一份北师大版八年级下册2 平行四边形的判定完美版课件ppt,文件包含623平行四边形的判定pptx、北师大版数学八年级下册第六章平行四边形62平行四边形的判定第3课时教学详案docx、62平行四边形的判定第三课时同步练习docx等3份课件配套教学资源,其中PPT共20页, 欢迎下载使用。














