人教版（2024）七年级下册（2024）8.1 平方根习题课件ppt

这是一份人教版（2024）七年级下册（2024）8.1 平方根习题课件ppt，文件包含81第3课时平方根ppt、81第3课时平方根习题doc、81第3课时平方根导学案doc等3份课件配套教学资源，其中PPT共26页， 欢迎下载使用。
1.了解平方根的概念，并理解平方与开平方的关系;2.会求非负数的平方根．（重点、难点）
1.什么叫做算术平方根？
（1）32= ，（－3）2= ；
（2） ， ；
（3）0.82= ，（－0.8）2= .
思考：反过来，如果已知一个数的平方，怎样求这 个数？
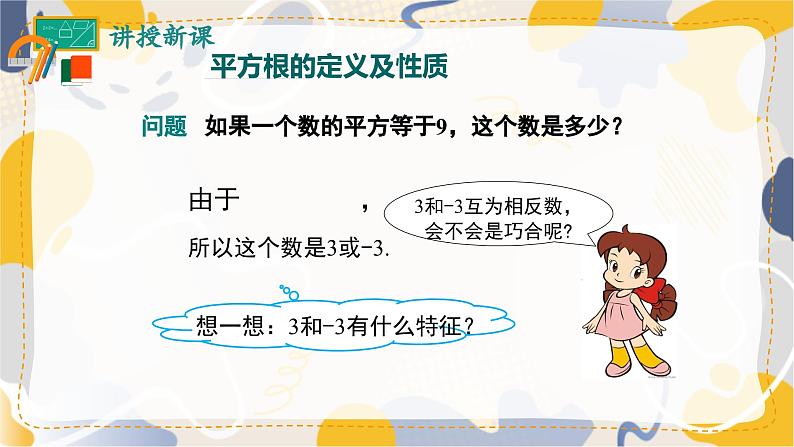
问题 如果一个数的平方等于9，这个数是多少？
由于 ，所以这个数是3或-3.
3和-3互为相反数，会不会是巧合呢?
(1) 4的平方等于16，那么16的算术平方根就是_____(2) 的平方等于 ，那么 的算术平方根就是____(3) 展厅地面为正方形，其面积是49 m2，则其边长为___m.
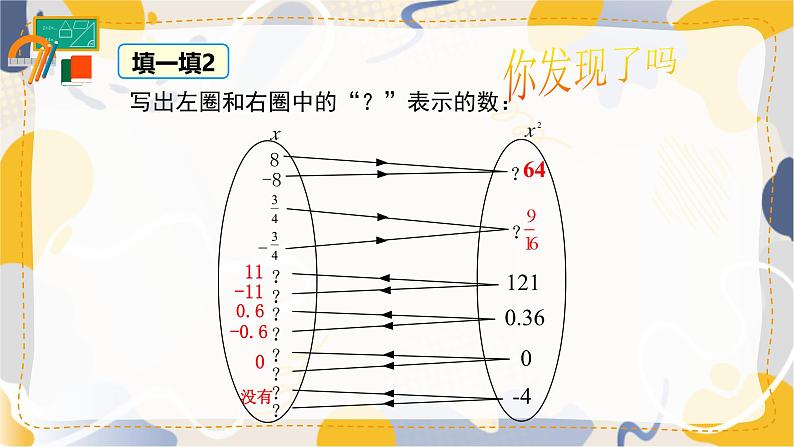
写出左圈和右圈中的“？”表示的数：
根据上述问题，即要找出一个数，使它的平方等于给定的数.我们抽象出下述概念：
如果有一个数x，使得x2=a，那么我们把x叫作a的一个平方根，也叫作二次方根.
例如： (±1)2=1，1的平方根为±1.　
1. 144的平方根是什么？
2. 0的平方根是什么？
4. -4有没有平方根？为什么？
没有，因为一个数的平方不可能是负数
通过这些题目的解答，你能发现什么?
问题：（1）正数有几个平方根？ （2）0有几个平方根？ （3）负数呢？
有没有一个数的平方是负数？
因为任何实数的平方都为非负数，所以负数没有平方根，也没有算术平方根.
平方根的性质： 1.正数有两个平方根，两个平方根互为相反数. 2.0的平方根还是0. 3.负数没有平方根.
判断下列说法是否正确，并说明理由．（1）49的平方根是7；（2）2是4的平方根；（3）-5是25的平方根；（4）64的平方根是±8；（5）-16的平方根是-4．
例1 一个正数的两个平方根分别是2a＋1和a－4， 求这个数．
解：由于一个正数的两个平方根是2a＋1和a－4， 则有2a＋1＋a－4＝0，即3a－3＝0， 解得a＝1. 所以这个数为(2a＋1)2＝(2＋1)2＝9.
方法归纳：一个正数有两个平方根，它们互为 相反数.
+1-1+2-2+3-3
已知一个数，求它的平方的运算，叫作平方运算.
反之，已知一个数的平方，求这个数的运算是什么？
求一个数的平方根的运算叫作开平方.
解 由于62=36，
因此36的平方根是6与-6.
解: 由于1.12=1.21，
因此1.21的平方根是1.1与-1.1.
一个非负数的平方根的表示方法：
三、平方根的数学符号表示
表示7的正的平方根（即算术平方根）
例3　求下列各式的值：
解：（1） ；
（2） ；
（3） .
1.包含关系：平方根包含算术平方根，算术平方根是平方根的一种.
平方根与算术平方根的联系与区别：
2.只有非负数才有平方根和算术平方根.
3. 0的平方根是0，算术平方根也是0.
1.个数不同：一个正数有两个平方根， 但只有一个算术平方根.
2.下列说法不正确的是______A.0的平方根是0 B. 的平方根是2C.非负数的平方根互为相反数D.一个正数的算术平方根一定大于这个数的相反数
1.下列说法正确的是_________① -3是9的平方根; ②25的平方根是5; ③ -36的平方根是-6; ④平方根等于0的数是0; ⑤64的算术平方根是8.
3. 判断下列说法是否正确.
（4）(-4)2的平方根是-4.