初中数学沪科版（2024）七年级下册（2024）6.1 平方根、立方根教案

这是一份初中数学沪科版（2024）七年级下册（2024）6.1 平方根、立方根教案，共5页。教案主要包含了知识技能类作业，综合拓展类作业等内容，欢迎下载使用。
《6.1.2立方根》教学设计
课型
新授课☑ 复习课☐ 试卷讲评课☐ 其他课☐
教学内容分析
《立方根》是沪科版七年级下册第6章《实数》的第一节第二课时的内容。《立方根》作为平方根内容的延伸和拓展。通过学习立方根，学生可以进一步理解开方运算的实质，同时立方根的学习也是后续学习更复杂的数学知识和解决实际问题的基础。它有助于学生理解数的立方与立方根之间的关系，掌握立方根的表示方法和计算方法，以及理解立方运算与开立方运算的互逆性。
学习者分析
学生在学习立方根时常常会遇到理解不透彻、计算不准确等问题。部分学生容易将立方根与平方根混淆，认为两者都是开方运算，但实际上立方根是求一个数的三次方等于给定值，而平方根是求一个数的二次方等于给定值。此外，学生对于立方根符号的理解也可能不足，误以为立方根就是三次方，而忽略了根号的意义。
学生的运算能力相对较弱，容易在计算过程中出现运算错误，如混淆立方根与平方根，或者在计算顺序上出错。同时，学生在实际应用立方根解决问题时的意识也较为薄弱，对于立方根在实际问题中的应用价值理解不够。
教学目标
1.了解立方根的概念，初步学会用根号表示一个数的立方根。
2.掌握开立方与立方互为逆运算，会用立方运算求某些数的立方根。
3.体会立方根与平方根的区别和联系。
4.经历观察、计算、小组讨论的过程，培养计算能力。
5.在探究立方根的概念和有关知识的过程中，体会类比数学思想，发展推理能力和有条理的语言表达能力。
教学重点
立方根的概念及求法。
教学难点
立方根与平方根的区别与联系，以及学生对立方根概念的深入理解。
学习活动设计
教师活动
学生活动
环节一：新知导入
教师活动1：
回顾：
1.什么是平方根？
2.什么是算术平方根？
3.平方根的性质有哪些？
教师讲授：
一般地，如果一个数的平方等于a，那么这个数叫做a的平方根，也叫做二次方根．
我们用a表示a的正的平方根，读作“根号a”，其中a叫做被开方数． 这个根也叫做a的算术平方根，另一个负的平方根记为−a ．
1.一个正数a的平方根有两个，它们互为相反数；
2.0的平方根是0，0的算术平方根也是0，即0=0 ；
3.负数没有平方根.
学生活动1：
认真思考回顾旧知
认真听讲，跟随教师回顾知识
活动意图说明：复习导入有利于衔接新旧知识，提高学习效率。通过旧知识引入新的知识有利于活跃课堂教学氛围，激发学生学习动机.
环节二：讲授新知
教师活动2：
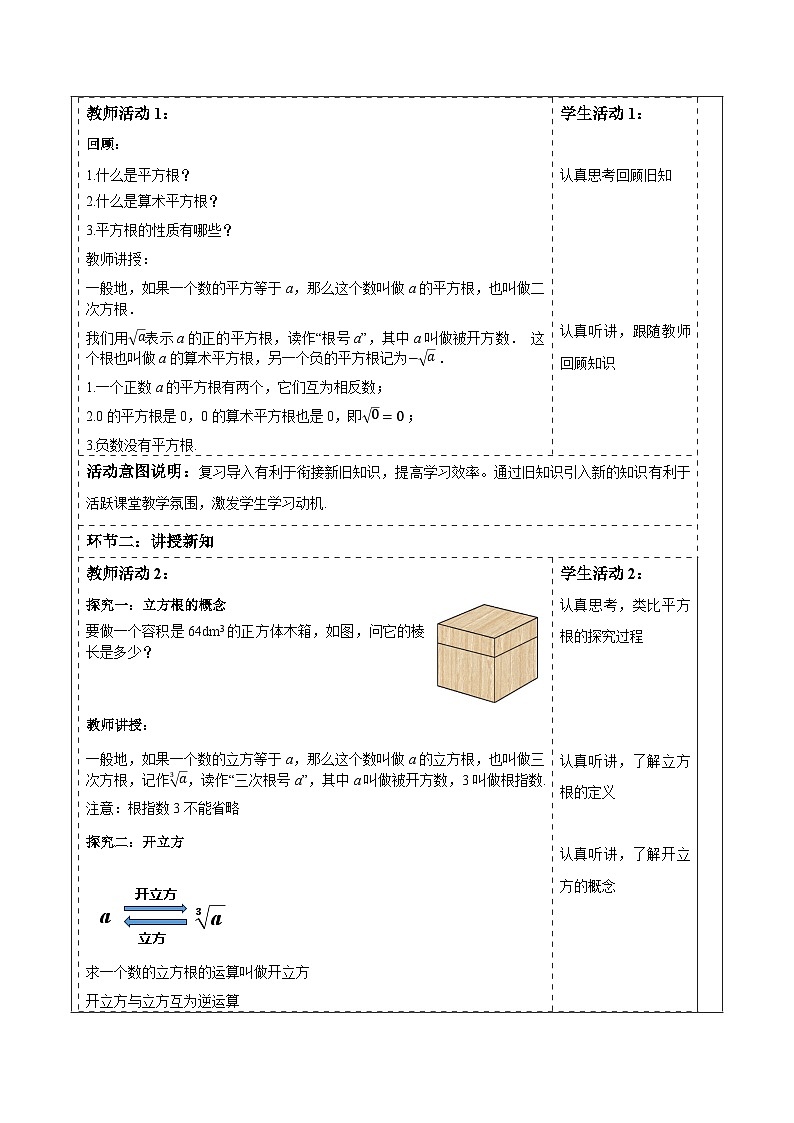
探究一：立方根的概念
要做一个容积是64dm3的正方体木箱，如图，问它的棱长是多少？
教师讲授：
一般地，如果一个数的立方等于a，那么这个数叫做a的立方根，也叫做三次方根，记作3a，读作“三次根号a”，其中a叫做被开方数，3叫做根指数.
注意：根指数3不能省略
探究二：开立方
a
3a
开立方
立方
求一个数的立方根的运算叫做开立方
开立方与立方互为逆运算
学生活动2：
认真思考，类比平方根的探究过程
认真听讲，了解立方根的定义
认真听讲，了解开立方的概念
活动意图说明：联系学生平时已经学过的类似的知识或者相似的已有的生活经验，帮助学生利用原有经验去更好地理解和把握新的知识。同时，类比还可以帮助学生更好地理解抽象概念和理论，使学习变得更加生动有趣。
环节三：例题精析
教师活动3：
例4求下列各数的立方根：
(1) 27; (2) −64; (3) 0.
解:
（1）因为33=27，所以27的立方根是3，即327=3．
（2）因为−43=−64，所以−64的立方根是−4，即3−64=−4．
（3）因为03=0，所以0的立方根是0， 30=0.
归纳：1.正数的立方根是一个正数；
2.负数的立方根是一个负数；
3.0的立方根是0.
思考：一般地，3−a=−3a对吗？
分析：
假设b3=a，则−b3=−a.
因为−b3=−b3=−a ，所以−a的立方根是−b，即3−a=−b．
因为b3=a ，所以a的立方根是b，即3a=b，则−3a = 3−a=−b ．
例5用计算器求下列各数的立方根（精确到0.01）：
(1)2 ； (2)7.797 ； (3)−17.456； (4)137398.
解 (1)在计算器上依次按键：，显示结果是1.259 921 05，精确到0.01，得32≈ 1.26．
(2)37.797≈1.98 .
(3)3−17.456≈−2.59 .
(4)3137398≈0.70 .
学生活动3：
学生认真思考，独立完成习题
学生认真听讲，了解立方根的性质
经历3−a=−3a的探究过程
学生认真思考，独立完成习题
学生认真听讲
活动意图说明：让学生通过具体例题的教学理解和巩固数学基础知识，把数学理论与实践相结合，掌握数学基础知识理论的用途和方法，从而达到提高分析问题解决问题的能力的目标。
环节四：课堂总结
教师活动4：
教师讲授：
立方根：一般地，如果一个数的立方等于a，那么这个数叫做a的立方根，也叫做三次方根，记作3a，读作“三次根号a”，其中a叫做被开方数，3叫做根指数.
立方根的性质：1.正数的立方根是一个正数；
2.负数的立方根是一个负数；
3.0的立方根是0.
学生活动4：
学生跟随教师对学习内容进行归纳梳理
活动意图说明：对课堂教学进行归纳梳理，给学生一个整体印象，促进学生掌握知识总结规律。
板书设计
课堂练习
【知识技能类作业】
必做题：
1.下列等式成立的是（ ）
A．3(−2)3=−2 B．81=±9 C．±25=5 D．(−2)2=−2
2.一个正方体的体积扩大为原来的8倍，则它的棱长为原来的（ ）
A．2倍 B．4倍 C．3倍 D．8倍
3.下列说法正确的是（ ）
A．−a一定没有平方根 B．立方根等于它本身的数是0，1
C．25的平方根是±5 D．−4的算术平方根是2
选做题：
4.如果 a 的平方根是±3，则3a−17 = ．
5.64的立方根是 .
6.根据下图中呈现的开立方运算关系，可以得出a的值为 .
【综合拓展类作业】
7.求下列各数的立方根:
(1)-0.001. (2)338. (3)(-5)3.
作业设计
【知识技能类作业】
必做题：
1.若x2=(−5)2，y3=(−5)3，则x−y的值为（ ）
A．0 B．±1 C．0或10 D．−5
2.下列说法正确的是 （ ）
A. 一个数的立方根有两个，它们互为相反数
B. 一个数的立方根比这个数的平方根小
C. 如果一个数有立方根，那么它一定有平方根
D. 3a与3−a互为相反数
3.若一个数的算术平方根与它的立方根相等，那么这个数是________.
【综合拓展类作业】
4.已知x是−64的立方根，y的算术平方根是13，求x+y的平方根．
教学反思
在设置问题情境引入立方根的概念时，缺乏足够的趣味性，对于部分注意力不够集中的学生，没有起到很好地引起无意注意的作用。此外，在学生对立方根的理解和应用能力方面，还需要进一步加强练习和指导，以提高他们的运算能力和实际应用能力。