初中数学新北师大版七年级下册第四章问题解决策略：特殊化教学课件2025春

这是一份初中数学新北师大版七年级下册第四章问题解决策略：特殊化教学课件2025春，共17页。
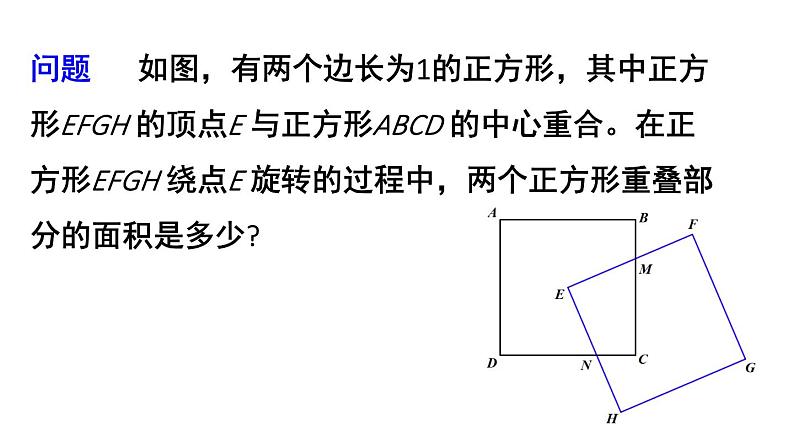
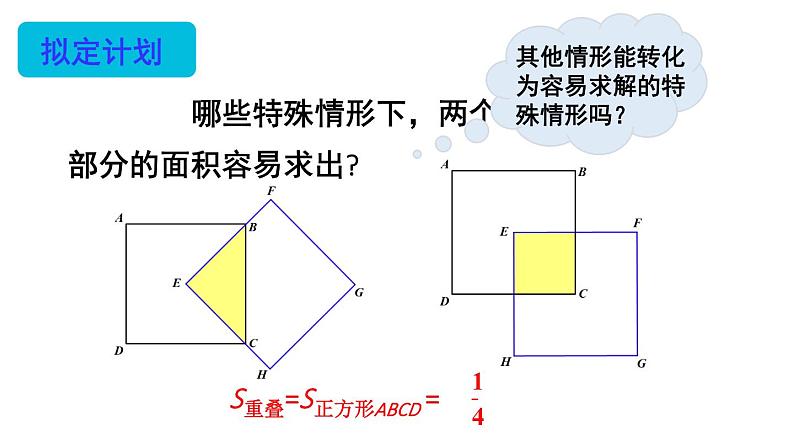
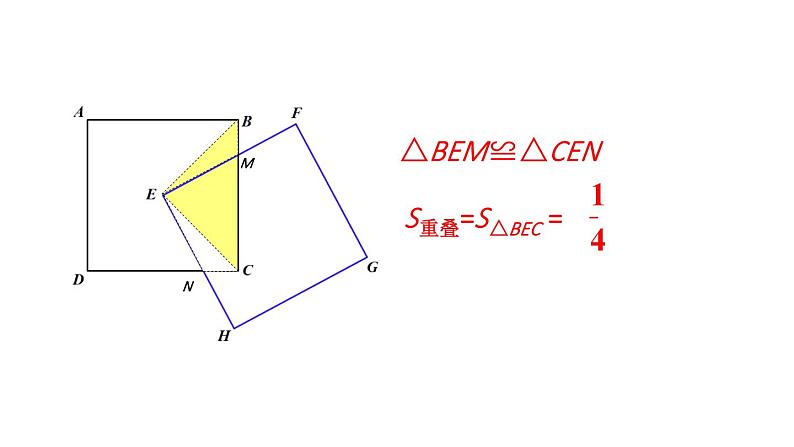
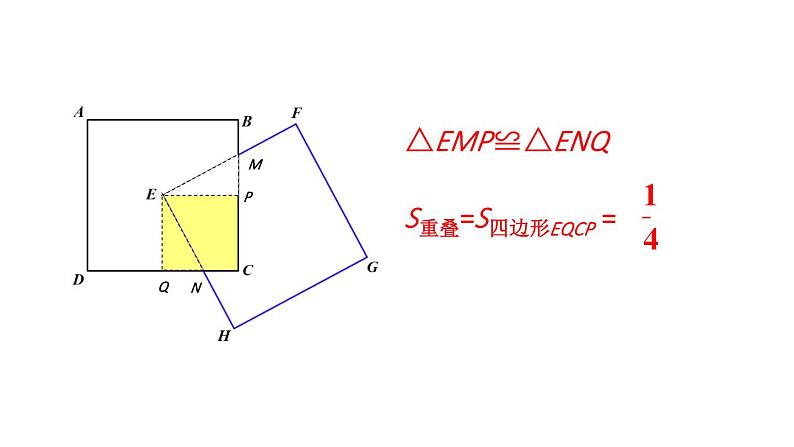
问题解决策略：特殊化北师大版七年级数学下册状元成才路状元成才路在讨论数学问题时，我相信特殊化比一般化起着更为重要的作用，这种方法是克服数学困难的最重要的杠杆之一．什么是特殊化?举个例子:三角形的三条中线交于一点等边三角形的三条中线交于一点一般性问题特殊情形 面对一般性的问题时，可以先考虑特殊情形，借助特殊情形下获得的结论或方法解决一般性的问题，这就是特殊化策略。问题 如图，有两个边长为1的正方形，其中正方形EFGH 的顶点E 与正方形ABCD 的中心重合。在正方形EFGH 绕点E 旋转的过程中，两个正方形重叠部分的面积是多少? 在旋转过程中，两个正方形的重叠部分会呈现哪些情形? 哪些特殊情形下，两个正方形重叠部分的面积容易求出?△BEM≌△CEN△EMP≌△ENQ 因为某些因素(如形状、位置或数值等)不确定，使得问题有多种情形时、可以限制这个引起变化的因素，考虑最为特殊的情形，采用从特殊情形入手的策略解决问题。问题思路受阻解：小颖是从以下特殊情形入手：点P为等边三角形ABC三条高的交点，如图所示。容易得到，△ABD≌ ACD，所以 BD = CD。同理可得 AF = BF， AE = CE。2.如图 ，四边形 ABCD 的面积是 16，各边中点分别为 M，N，P，Q，MP与 NQ 相交于点 O，求图中阴影部分的面积。解：如图，连接OA，OB，OC，OD。因为 M是AB的中点，同理可得，S阴影 = S△OAM + S△OAQ + S△OCN + S△OCP3.甲、乙两人轮流在一张圆桌上放置同样大小的硬币，每人每次只能置一枚硬币，且放置过程中不允许重叠与倾斜，硬币不能超出桌面的边界。规定谁在桌上放下最后一枚便币，谁就获胜。你知道获胜的策略吗?解：甲有必胜策略，即先放置一枚硬币在桌面中心，之后每次在乙放置硬币位置的对称位置放置硬币，直到桌面无法再放置更多硬币，甲将获胜。4.一个三位数除以它的各位数字之和，商最大是多少?先考虑特殊情形，固定a，b的值，如a = 1， b = 1同理，固定a，c的值时，b = 0时 S 最大；固定b，c的值时，a = 9 时 S 最大。状元成才路状元成才路 面对一般性的问题时，可以先考虑特殊情形，借助特殊情形下获得的结论或方法解决一般性的问题，这就是特殊化策略。1.完成课本的相应练习题，2.完成练习册本课时的习题。