中考数学总复习举一反三系列(通用版)专题20矩形、菱形、正方形(10个高频考点)(强化训练)(全国通用)(原卷版+解析)

这是一份中考数学总复习举一反三系列(通用版)专题20矩形、菱形、正方形(10个高频考点)(强化训练)(全国通用)(原卷版+解析)，共119页。
1．（2022·湖南湘西·统考中考真题）如图，在Rt△ABC中，∠A＝90°，M为BC的中点，H为AB上一点，过点C作CG∥AB，交HM的延长线于点G，若AC＝8，AB＝6，则四边形ACGH周长的最小值是（ ）
A．24B．22C．20D．18
2．（2022·四川乐山·统考中考真题）如图，等腰△ABC的面积为23，AB=AC，BC=2．作AE∥BC且AE=12BC．点P是线段AB上一动点，连接PE，过点E作PE的垂线交BC的延长线于点F，M是线段EF的中点．那么，当点P从A点运动到B点时，点M的运动路径长为（ ）
A．3B．3C．23D．4
3．（2022·湖北宜昌·统考中考真题）如图，在矩形ABCD中，E是边AD上一点，F，G分别是BE，CE的中点，连接AF，DG，FG，若AF=3，DG=4，FG=5，矩形ABCD的面积为________．
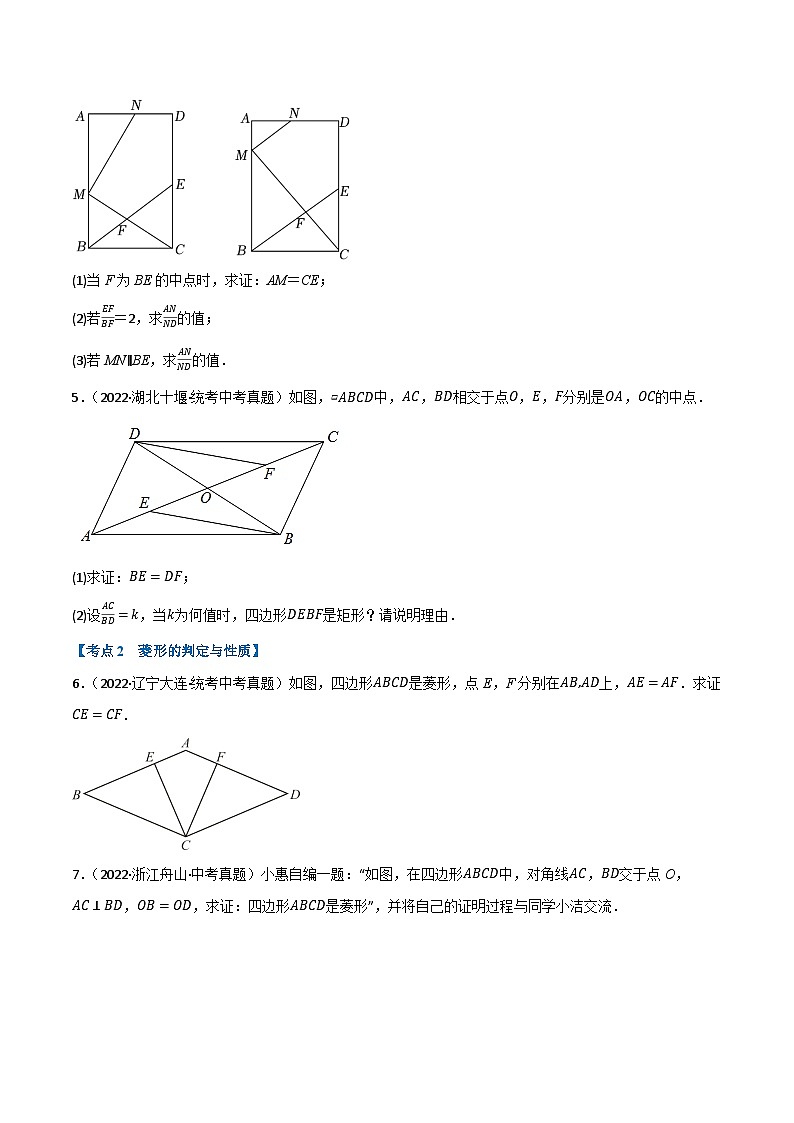
4．（2022·四川内江·统考中考真题）如图，在矩形ABCD中，AB＝6，BC＝4，点M、N分别在AB、AD上，且MN⊥MC，点E为CD的中点，连接BE交MC于点F．
(1)当F为BE的中点时，求证：AM＝CE；
(2)若EFBF＝2，求ANND的值；
(3)若MN∥BE，求ANND的值．
5．（2022·湖北十堰·统考中考真题）如图，▱ABCD中，AC，BD相交于点O，E，F分别是OA，OC的中点．
(1)求证：BE=DF；
(2)设ACBD=k，当k为何值时，四边形DEBF是矩形？请说明理由．
【考点2 菱形的判定与性质】
6．（2022·辽宁大连·统考中考真题）如图，四边形ABCD是菱形，点E，F分别在AB,AD上，AE=AF．求证CE=CF．
7．（2022·浙江舟山·中考真题）小惠自编一题：“如图，在四边形ABCD中，对角线AC，BD交于点O，AC⊥BD，OB=OD，求证：四边形ABCD是菱形”，并将自己的证明过程与同学小洁交流．

若赞同小惠的证法，请在第一个方框内打“√”；若赞成小洁的说法，请你补充一个条件，并证明．
8．（2022·山西吕梁·统考三模）综合与实践：
数学活动课上，老师让同学们根据下面情境提出问题并解答．
问题情境：在□ABCD中，点P是边AD上一点．将△PDC沿直线PC折叠，点D的对应点为E．
“兴趣小组”提出的问题是：如图1，若点P与点A重合，过点E作EF∥AD，与PC交于点F，连接DF，则四边形AEFD是菱形．
(1)数学思考：请你证明“兴趣小组”提出的问题；
(2)拓展探究：“智慧小组”提出的问题是：如图2，当点P为AD的中点时，延长CE交AB于点F，连接PF．试判断PF与PC的位置关系，并说明理由．
请你帮助他们解决此问题．
(3)问题解决：“创新小组”在前两个小组的启发下，提出的问题是：如图3，当点E恰好落在AB边上时，AP=3，PD=4，DC=10．则AE的长为___________．（直接写出结果）
9．（2022·黑龙江哈尔滨·统考一模）如图矩形ABCD中，对角线BD的垂直平分线MN与AD相交于点M，与BD相交于点O，与BC相交于N，连接MB、DN；
(1)求证：四边形BMDN是菱形；
(2)若tan∠AMB=43，ON=5，求△BMD的面积．
10．（2022·浙江宁波·统考二模）如图1，平行四边形ABCD中，AB=9，BC=12，点P是BC边上的点，连结AP，以AP为对称轴作△ABP的轴对称图形△AQP．
(1)如图2，当点Q正好落在AD边上时，判断四边形ABPQ的形状并说明理由；
(2)如图1，当点P是线段BC的中点且CQ=4时，求AP的长；
(3)如图3，当点P,Q,D三点共线时，恰有∠PQC=∠PQA，求BP的长．
【考点3 正方形的判定与性质】
11．（2022·海南海口·海南华侨中学校联考模拟预测）如图①，在正方形ABCD中，点E、F、G、H分别在边AB、BC、CD、DA上，若EG⊥FH，
(1)求证：EG=FH；
(2)如果把题目中的“正方形”改为“长方形”、若AB=3，BC=4（如图②），求FHEG的值；
(3)如果把题目中的“EG⊥FH”改为“EG与FH的夹角为45°”（如图③），若正方形ABCD的边长为2，FH的长为5，求EG的长．
12．（2022·山东济南·统考模拟预测）（1）【问题情境】如图1，四边形ABCD是正方形，点E是AD边上的一个动点，以CE为边在CE的右侧作正方形CEFG，连接DG、BE，则DG与BE的数量关系是______；
（2）【类比探究】如图2，四边形ABCD是矩形，AB=2，BC=4，点E是AD边上的一个动点，以CE为边在CE的右侧作矩形CEFG，且CG:CE=1:2，连接DG、BE．判断线段DG与BE有怎样的数量关系和位置关系，并说明理由；
（3）【拓展提升】如图3，在（2）的条件下，连接BG，则2BG+BE的最小值为______．
13．（2022·贵州贵阳·统考二模）如图，已知四边形ABCD是正方形，AB＝42，点E为对角线AC上一动点，连接DE，过点E作EF⊥DE，交射线BC于点F，以DE，EF为邻边作矩形DEFG，连CG．
(1)求证：矩形DEFG为正方形；
(2)求证：CE＋CG＝8
14．（2022·贵州黔西·统考中考真题）如图1，在正方形ABCD中，E，F分别是BC，CD边上的点（点E不与点B，C重合），且∠EAF=45°．
(1)当BE=DF时，求证：AE=AF；
(2)猜想BE，EF，DF三条线段之间存在的数量关系，并证明你的结论；
(3)如图2，连接AC，G是CB延长线上一点，GH⊥AE，垂足为K，交AC于点H且GH=AE．若DF=a，CH=b，请用含a，b的代数式表示EF的长．
15．（2022·四川德阳·模拟预测）已知：四边形ABCD是正方形，点E在CD边上，点F在AD边上，且AF=DE．

(1)如图1，AE与BF有怎样的关系．写出你的结果，并加以证明；
(2)如图2，对角线AC与BD交于点O．BD，AC分别与AE，BF交于点G，点H．
①求证：OG=OH；
②连接OP，若AP=4，OP=2，求AB的长．
【考点4 特殊四边形中的折叠变换】
16．（2022·吉林长春·统考二模）【感知】如图①，Rt△ABC中，∠C=90°，AC=12AB，易知∠B=30°（不需要证明）．
【探究】如图②，四边形ABCD是一张边长为2的正方形纸片，E、F分别为AB、CD的中点，沿过点D的折痕将纸片翻折，使点A落在EF上的点A'处，折痕交AE于点G，求∠ADG的度数和AG的长．
【拓展】若矩形纸片ABCD按如图③所示的方式折叠，B、D两点恰好重合于一点O（如图④），若AB=6，直接写出EF的长．
17．（2022·吉林长春·模拟预测）【推理】
如图1，在边长为10的正方形ABCD中，点E是CD上一动点，将正方形沿着BE折叠，点C落在点F处，连结BE，CF，延长CF交AD于点G，BE与CG交于点M．
(1)求证：CE=DG．
【运用】
(2)如图2，在【推理】条件下，延长BF交AD于点H．若CE=6，求线段DH的长．
【拓展】
(3)如图3，在【推理】条件下，连结AM．则线段AM的最小值为 ．
18．（2022·河南信阳·统考模拟预测）学习了菱形的判定后，小张同学与小刘同学讨论探索折纸中的菱形．
小张：如图①，两张相同宽度的矩形纸条重叠部分（阴影部分）是一个菱形．
小刘：如图②，一张矩形纸条沿EG折叠后，重叠部分展开（阴影部分）后是一个菱形．
(1)小张同学的判断是否正确？
(2)小刘同学的判断是否正确？如果正确，以小刘的方法为例，证明他的判断；如果不正确，请说明理由．
(3)如图③，矩形ABCD的宽AB=4，若AE=2AB，沿BE折叠后，重叠部分展开（阴影部分）后得到菱形GBFE，求菱形GBFE的面积．
19．（2022·云南昆明·云大附中校考三模）综合与实践
在数学教学中，教师和学生都学习到了新知识，掌握了许多新技能．例如教材八年级下册的数学活动——折纸，就引起了许多同学的兴趣．在经历图形变换的过程中，进一步发展了同学们的空间观念，积累了数学活动经验．
实践发现：
对折矩形纸片ABCD，使AD与BC重合，折痕为EF，把纸片展平：再一次折叠纸片，使点A落在EF上的点N处，并使折痕经过点B，折痕为BM，把纸片展平，连接AN，如图①；
(1)折痕BM所在直线是否是线段AN的垂直平分线？请判断图中△ABN是什么特殊三角形？请写出解答过程．
(2)继续折叠纸片，使点A落在BC边上的点H处，并使折痕经过点B，得到折痕BG，把纸片展平，如图②，求∠GBN的度数．
(3)拓展延伸：
如图③，折叠矩形纸片ABCD，使点A落在BC边上的点A′处，并且折痕交BC边于点T，交AD边于点S，把纸片展平，连接AA′交ST于点O，连接AT；求证：四边形SATA′是菱形．
20．（2022·湖北武汉·校考三模）（1）如图1，在正方形ABCD中，E是CD上一动点，将正方形沿着BE折叠，点C落在点F处，连接CF，并延长CF交AD于点G．求证：△BCE≌△CDG；
（2）在（1）的条件下，如图2，延长BF交AD边于点H．若CEBC=23，求GHDH的值；
（3）如图3，四边形ABCD为矩形，同样沿着BE折叠，连接CF，延长CF，BF分别交AD于G，H两点，若ABBC=34,DHGH=45，则DEEC的值为___________．（直接写出结果）
【考点5 特殊四边形中的平移变换】
21．（2022·安徽合肥·合肥市第四十五中学校考三模）我们把连接菱形对边中点得到的所有菱形称作如图①所示基本图的特征图形显然这样的基本图共有5个特征图形．将此基本图不断复制并平移，使得相邻两个基本图的一个顶点与对称中心重合，这样得到图1、图2、图3…
(1)观察以上图形并完成下表：
猜想：在图n中，特征图形的个数为______；（用含n的式子表示）
(2)已知基本图的边长为4，一个内角恰好为60°，求图20中所有特征图形的面积之和．
22．（2022·福建厦门·厦门双十中学校考二模）如图，四边形ABCD是矩形，平移线段AB至EF，其中点A的对应点为点E，点B的对应点为点F，且点E恰好落在边BC上．
(1)若AF＝DF，求证：点E为BC中点；
(2)若BC＝k AB，2＜k＜2，是否存在∠BFC＝90°？请说明理由．
23．（2022·云南德宏·统考模拟预测）如图，将△ABC沿射线AB平移4cm后能与△BDE完全重合，连接CE、CD交BE于点O，OB＝OC．
(1)求证：四边形CBDE为矩形；
(2)若S△BOC＝433cm2，求∠ACD的度数．
24．（2022·山东淄博·统考二模）已知，矩形ABCD，点E在AB上，点G在AD，点F在射线BC上，点H在CD上．
(1)如图1，当矩形ABCD为正方形时，且DE⊥GF，求证：BF=AE+AG；
(2)在（1）的条件下，将GF沿AD向右平移至点G与点D重合，如图2，连接EF，取EF的中点P，连接PC，试判断BE与PC的数量关系，并说明理由；
(3)如图3，点F在BC上，连接EH，EH交FG于O，∠GOH=45°，若AB=2，BC=4，FG=5，求线段EH的长．
25．（2022·辽宁沈阳·统考一模）已知正方形ABCD，在边DC所在的直线上有一动点E，连接AE，一条与射线AE垂直的直线l沿射线AE方向，从点A开始向上平移，垂足为点P，交边AD所在直线于点F．
(1)如图1所示，当直线l经过正方形ABCD的顶点B时．求证：AF=DE；
(2)如图2所示，当直线l经过AE的中点时，与对角线BD交于点G，连接EG，CG．求证：GE=GC；
(3)直线l继续向上平移，当点P恰好落在对角线BD所在的直线上时，交边CB所在的直线于点H，当AB=3，DE=1，请直接写出BH的长．
【考点6 特殊四边形中的旋转变换】
26．（2022·江苏南通·统考中考真题）如图，矩形ABCD中，AB=4,AD=3，点E在折线BCD上运动，将AE绕点A顺时针旋转得到AF，旋转角等于∠BAC，连接CF．
(1)当点E在BC上时，作FM⊥AC，垂足为M，求证AM=AB；
(2)当AE=32时，求CF的长；
(3)连接DF，点E从点B运动到点D的过程中，试探究DF的最小值．
27.（2022·江西·统考中考真题）问题提出：某兴趣小组在一次综合与实践活动中提出这样一个问题：将足够大的直角三角板PEF∠P=90°,∠F=60°的一个顶点放在正方形中心O处，并绕点O逆时针旋转，探究直角三角板PEF与正方形ABCD重叠部分的面积变化情况（已知正方形边长为2）．
(1)操作发现：如图1，若将三角板的顶点P放在点O处，在旋转过程中，当OF与OB重合时，重叠部分的面积为__________；当OF与BC垂直时，重叠部分的面积为__________；一般地，若正方形面积为S，在旋转过程中，重叠部分的面积S1与S的关系为__________；
(2)类比探究：若将三角板的顶点F放在点O处，在旋转过程中，OE,OP分别与正方形的边相交于点M，N．
①如图2，当BM=CN时，试判断重叠部分△OMN的形状，并说明理由；
②如图3，当CM=CN时，求重叠部分四边形OMCN的面积（结果保留根号）；
(3)拓展应用：若将任意一个锐角的顶点放在正方形中心O处，该锐角记为∠GOH（设∠GOH=α），将∠GOH绕点O逆时针旋转，在旋转过程中，∠GOH的两边与正方形ABCD的边所围成的图形的面积为S2，请直接写出S2的最小值与最大值（分别用含α的式子表示），
（参考数据：sin15°=6−24,cs15°=6+24,tan15°=2−3）
28．（2022·辽宁鞍山·模拟预测）如图，正方形ABCD中，点E，F，G分别为边AB，BC，AD上的点，且AE=BF=DG，连接EF，GE，GF．
(1)△BEF可以看成是△AGE绕点M逆时针旋转α角所得，请在图中画出点M，并直接写出α角的度数；
(2)当点E位于何处时，△EFG的面积取得最小值？请说明你的理由；
(3)试判断直线CD与△EFG外接圆的位置关系，并说明你的理由．
29．（2022·山东枣庄·校考模拟预测）如图1，在等腰直角三角形ADC中，∠ADC=90°，AD=4．点E是AD的中点，以DE为边作正方形DEFG，连接AG，CE．将正方形DEFG绕点D顺时针旋转，旋转角为α（0°